ЗАДАНИЕ НА КУРСОВУЮ РАБОТУ
Задание на курсовую работу состоит из двух частей. Первая часть представляет собой совокупность типовых задач базового уровня [1]. Вторая часть является расчетной частью курсовой работы В этой части работы предполагается построение по заданной статистической информации простейшей математической модели, описывающей типичную экономическую ситуацию, встречающуюся в практической деятельности менеджера. Cтудент, используя методы, изучаемые в курсе математики, определяет по исходным данным коэффициенты модели и оптимальные значения интересующих экономических параметров.
Для каждого студента определен индивидуальный набор заданий. Номер варианта соответствует порядковому номеру 
студента в списке его группы Курсовая работа выполняется в печатной форме аккуратно на одной стороне листа стандартного формата. Графики строятся черными или цветными карандашами средней твердости на обычной или миллиметровой бумаге. Листы с текстом курсового проекта и графики должны быть сшиты.
Текст работы должен содержать все необходимые расчеты и пояснения В курсовой работе обязательно наличие титульного листа и сквозная нумерация всех листов. Образец титульного листа содержится в приложении.
Теория вероятностей и математическая статистика.
Задача № 1 ( [1], стр 8)
При перевозке 100+ 
деталей, из которых 1+ 
были забракованы, утеряна 1 стандартная деталь. Найти вероятность того, что наудачу извлеченная деталь окажется нестандартной.
Задача № 2 ( [1], стр 10)
В ящике 20+ деталей, из которых 3+ окрашены. Рабочий наудачу взял 3 детали. Найти вероятность того, что хотя бы одна из взятых детадей окрашена.
Задача № 3 ( [1], стр 13, задача 26)
В точке С, положение которой на телефонной линии, соединяющей города А и Б равновозможно, произошел разрыв. Найти вероятность, что точка С удалена более чем на 15+ км. от каждого из городов, если расстояние между ними 50+2 км.
Задача № 4 ( [1], стр 24)
1.Из 60+ вопросов, входящих в экзаменационные билеты, студент подготовил 50+ . Какова вероятность того, что взятый наудачу студентом билет, содержащий 3 вопроса, будет состоять из подготовленных им вопросов?
.
Задача № 5 ( [1], стр 33)
Два автомата производят одинаковые детали, которые поступают на общий конвейер. Производительность первого автомата вдвое больше производительности второго. Первый автомат производит (55+ )% деталей отдичного качества, а второй: (65+ )%. Наудвчу взятая с конвейера деталь оказалась отличного качества. Найти вероятность того, что эта деталь произведена первым автоматом.
Задача № 6 ( [1], стр 38)
Монету бросают 5+ раз. Найти вероятность того,что «герб» выпадет не менее, чем 1+ раз Составить ряд распределения числа появлений «герба» в 5+ испытаниях.
Задача № 7 ( [1], стр133)
Даны независимые случайные величины X и Y заданы своими рядами распределений:
| ||
| 0,7 | 0,3 |
| 1+ 
| ||
| 0,4 | 0,6 |
Составить закон распределения их суммы - случайной величины Z=X+Y и проверить выполнение свойства математического ожидания:
М(X+Y)=M(X) + M(Y)
Задача № 8 ( [1], стр 91)
Задана функция распределения непрерывной случайной величины Х:
Найти плотность вероятности распределения случайной величины Х
Задача № 9 ( [1], стр 53)
Устроство состоит из трех независимо работающих элементов. Вероятность отказа каждого элемента в одном опыте равна 
. Составить закон заспределения числа отказавших элементов в одном опыте
Задача № 10 ( [1], стр 58)
Завод отправил на базу 1000 изделий. Вероятность повреждения изделия в пути равна 0,001. Найти вероятности того, что в пути будетповреждено изделий: а) ровно три; б) менее трех; в)хотя бы одно.
Задача № 11 ( [1], стр 62)
Среднее число вызовов такси, поступающих на диспетчерский пукт в одну минуту, равно .Найти вероятность того, что за две минуты поступит: а) менее, чем +1 вызовов; б) ровно +1 вызовов.
Задача № 12 ( [1], стр 72)
Найти дисперсию дискретной случайной велчины Х – числа появлений события А в двух независимых испытаниях, если вероятности появления события в этих испытаниях одинаковы и известно, что М(Х)=1+0,01 .
Задача № 13 ( [1], стр 106)
Цена деления шкалы прибора равна 0,1 Показания прибора округляют до ближайшего деления. Найти плотность равномерного распределения ошибки округления и вероятнсть того,что при измерении будет сделана ошибка, превышающая 0,02
Задача № 14 ( [1], стр 62)
К киоску покупатели подходят в среднем через каждые 
минут. Киоск начинает работу в 9 часов утра. Считая поток покупателей простейшим, найти вероятность того, что между 3 и 4 покупателем (от начала рабочего дня) пройдет: а) не менее 
минут; б) от 
до 
минут.
Задача № 15 ( [1], стр. 110)
Случайная величина имеет нормальное распределение с математическим ожиданием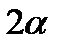 
и средним квадратическим отклонением 
. Найти вероятность того, что ее значение
а) будет отрицательным;
б) будет лежать в интервале от -1 до 3;
Задача № 16 ( [1], стр 113)
В результате измерения массы большого числа яблок некоторого сорта установлено, что масса одного яблока лежит в пределах от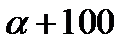 
до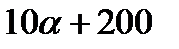 
граммов. Считая, что масса яблока – случайная величина, имеющая нормальное распределение, и используя правило «трех сигм», найти математическое ожидание и с.к.о. массы яблока. Найти вероятность того, что масса случайно выбранного яблока больше 
граммов.
Задача № 17 ( [1], стр 152, 153)
Проведена серия из 15 экспериментов со случайной величиной X. По результатам наблюдений получена выборка значений этой случайной величины. Для 
(первый вариант курсовой работы) эта выборка имеет вид: 
. Для любого варианта с номером 
выборка выглядит так 
, т.е. к каждому элементу выборки первого варианта прибавляется число, равное номеру варианта, уменьшенному на единицу. Например, если 
, то выборка выглядит так: 
.
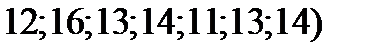По данной выборке требуется: 1) построить дискретный вариационный ряд; 2) определить численное значение моды 
и медианы 
; 3) построить ряд распределения частот 4) построить выборочную функцию распределения и ее график; 5) найти несмещенную оценку генеральной средней; 6) найти смещенную и несмещенную оценки генеральной дисперсии (т.е. выборочную дисперсию и исправленную выборочную дисперсию) и соответствующие оценки среднего квадратичного отклонения.
