СТАТИСТИЧЕСКОЕ ИЗУЧЕНИЕ ВЗАИМОСВЯЗИ
Виды связей
Исследование объективно существующих связей между явлениями -важнейшая задача теории статистики. Статистика разработала множество методов изучения связей, выбор которых зависит от поставленных задач. Связи между явлениями ввиду их большого разнообразия классифицируются по ряду оснований. Признаки по их значению для изучения взаимосвязи делятся на два класса.
Факторные (факторы) – это такие признаки, которые оказывают влияние и вызывают изменение других, связанных с ними признаков. Признаки, которые меняются под влиянием факторных, называются результативными.
Существует два основных вида связей:
- функциональные,
- стохастические.
Функциональные связи являются точными и полными. Это такие связи, когда каждому значению факторного признака соответствует единственное значение результативного признака. Выражаются эти связи в виде формулы.
Например, зависимость площади круга от его диаметра:
Ѕ=π×R2.
Здесь R – факторный признак, S – результативный.
Такие связи в общественной жизни, экономике встречаются крайне редко.
В массовых общественных явлениях проявляются зависимости распределения результативного признака в зависимости от одного или нескольких признаков-факторов. Такие связи называются стохастическими.
Частным случаем стохастических связей являются связи корреляционные, когда под действием одного или нескольких признаков-факторов меняется среднее значение результативного признака.
Особенностью корреляционных связей является то, что эти связи требуют массовых наблюдений и являются неполными.
Различают следующие виды связей:
1) в зависимости от направления действия различают связи прямые (прямопропорциональная зависимость) и обратные (обратно-пропорциональная зависимость);
2) по аналитическому выражению различают связи прямолинейные и криволинейные.
Прямолинейные – это такие связи, когда величина результативного признака меняется равномерно под влиянием признака-фактора.
Например: y=ax+b;
3) в зависимости от количества выбранных факторов различают связи однофакторные (парные) и многофакторные, когда факторов два и более.
Измерение тесноты связи между атрибутивным признаками
В статистической практике приходится сталкиваться с задачами измерения связи между качественными признаками. Для этого статистической наукой разработаны методы, которые называются непараметрическими.
Коэффициент взаимной сопряженности Чупрова и Пирсона
Коэффициент взаимной сопряженности Чупрова и Пирсона применяется тогда, когда исследуется теснота связи между варьированием двух атрибутивных признаков, когда это варьирование образует 3 и более группы по каждому признаку.
Коэффициенты принимают значения от 0 до 1, и чем ближе к 1, тем теснее связь.
Этот метод обычно используется для установления характера связи при относительно небольшом числе наблюдений. С помощью этого приема можно дать самую общую характеристику связи посредством сравнения факторного и результативного признаков.
Коэффициент взаимной сопряженности Пирсона вычисляется по формуле:
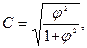
где φ2 – показатель взаимной сопряженности.
Коэффициент взаимной сопряженности Чупрова вычисляется по следующей формуле:

где φ2 – показатель взаимной сопряженности,
m1 – количество групп по первому признаку,
m2 – количество групп по второму признаку.
Коэффициент Чупрова всегда меньше коэффициента Пирсона. Он дает обычно более осторожную оценку связи.
Пример: (для нахождения показателя взаимной сопряженности).
Таблица 10.1 – Распределение предприятий по техническому и организационному уровню развития
| Орг. уровень Тех. уровень | Ниже среднего | Средний | Выше среднего | Всего |
| Ниже среднего | 3,27 (49) | 3,2 (64) | 5,6 (100) | 12,07 0,4828 |
| Средний | 1,07 (16) | 2,45 (49) | 0,056 (1) | 3,576 0,298 |
| Выше среднего | 1,07 (16) | 1,25 (25) | 2,72 (49) | 5,04 0,315 |
| Итого: | 1,0958= φ2+1 |
1) Каждую частоту возведем в квадрат и запишем соответствующий результат в скобках.
2) Делим число, стоящее в скобках, на величину в итоговой строке.
3) Числа, полученные во втором пункте, складываем по строкам и записываем в графу «Итого»: 3,27+3,2+5,6=12,07.
4) В графе «Итого» делим второе число на первое и результат записываем в эту же графу: 12,07/25=0,4898.
5) Результаты, полученные в 4-м пункте, складываем и записываем в правом нижнем углу таблицы.
φ2= 1,0958-1=0,0958 – показатель взаимной сопряженности.

 .
.
Связь незначительная.






