1. Исследование детерминированных периодических сигналов.
2. Исследование детерминированных непериодических сигналов.
3. Исследование корреляционной функции случайных сигналов.
4. Исследование спектральной плотности случайных сигналов.
5. Исследование амплитудной модуляции сигналов.
6. Исследование квантования сигналов по времени.
7. Исследование квантования сигналов по уровню.
8. Исследование метода накопления при приеме сигналов.
9. Исследование критерия максимального правдоподобия.
10. Исследование критерия максимума апостериорной вероятности.
11. Исследование критерия идеального наблюдателя.
12. Исследование методов эффективного кодирования сообщений.
13. Исследование методов задания линейных систематических кодов.
14. Исследование процесса обнаружения и исправления ошибок избыточными кодами.
15. Алгоритм выбора образующего полинома циклического кода.
16. Исследование помехоустойчивости циклических кодов.
17. Исследование кодирующих устройств циклических кодов.
18. Исследование декодирующих устройств циклических кодов.(делится на полином, проверяется есть ли ошибка, остаток проверяется)
19. Исследование алгоритма работы системы РОС-ОЖ.
20. Исследование алгоритма работы системы РОС-НК.
21. Исследование алгоритма работы системы РОС-АП.
Пример выполнения курсово РАБОТЫ
Тема курсовой работы “Исследование помехоустойчивости циклических кодов” посвящена выбору образующих полиномов циклических кодов и оценке кратности обнаруживаемых ошибок и помехоустойчивости при их применении.
РЕФЕРАТ
Пояснительная записка данной работы содержит 22 страницы, 4 рисунка и 2 таблицы.
Ключевые слова: циклические коды, информационные разряды, дополнительные разряды, допустимое значение вероятности не обнаружения ошибок, вероятность искажения кодовой комбинации, кратность гарантийно обнаруживаемых ошибок, характер канала связи, образующий полином, перемножение полиномов.
Для поиска ошибок при передаче сигналов, каждую кодовую комбинацию k-элементного безызбыточного кода, выраженной в виде многочлена, перемножаем на образующий полином. При этом перемножение производится по обычным правилам алгебры с приведением подобных членов по модулю два. Следовательно, в случае отсутствия ошибок любая разрешенная кодовая комбинация циклического кода должна разделиться на образующий полином без остатка. Задачей данной работы является нахождение образующего полинома в двоичной системе счисления, удовлетворяющего заданной вероятности не обнаружения ошибок.
Введение
В настоящее время информация стала фактором, определяющим эффективность любой сферы деятельности. Увеличились информационные потоки и повысились требования к скорости передачи данных, одним из факторов повышения скорости передачи данных служит метод кодирования. Также появилась потребность исправления ошибок, не после повторной передачи кода, а с помощью более точных методов обнаружения ошибок на принимающей стороне. Стали разрабатываться универсальные методы обнаружения ошибок, одним из которых является метод циклических кодов, который обеспечивает надежность передачи данных.
В работе реализуется алгоритм нахождения необходимого полинома и оценивается помехоустойчивость полученного циклического кода.
1 Циклические коды
Наиболее распространенным классом линейных кодов являются циклические коды. Это обусловлено относительно простым построением кодера и декодера, обнаруживающего ошибки, при достаточно высоких корректирующих способностях кода. Эти коды позволяют преодолеть некоторые трудности, связанные с технической реализацией и свойственные линейным кодам.
Задание циклических кодов
Алгебраическая структура циклических кодов впервые была исследована Боузом, Чоудхури и Хоквингемом, поэтому они известны как БЧХ-коды.
Эти коды характеризируются следующими свойствами:
– длина кодовых последовательностей
| (1.1) |
где m=1, 2, 3, …;
– число проверочных единичных элементов не превышает величины 
, т. е.
| (1.2) |
– код обнаруживает все пачки ошибок длины
| (1.3) |
– циклический сдвиг разрешенной кодовой комбинации кода приводит к образованию разрешенной комбинации этого же кода. Воспользуемся более простыми методиками, базирующимися на алгебраических понятиях. В этом случае более удобной является запись кодовых комбинаций в виде многочлена переменной 
:
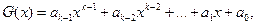
| (1.4) |
где основание системы счисления.
Коэффициенты 
представляют собой цифры данной системы счисления. В двоичной системе счисления коэффициенты могут принимать одно из двух значений: 0 или 1. Так, например, двоичное четырехразрядное число 1001 может быть записано в виде полинома
|
Это выражение устанавливает однозначное соответствие между двумя формами записи кодовых комбинаций.
Циклические коды образуются путем умножения каждой кодовой комбинации k -элементного безызбыточного кода, выраженной в виде многочлена G(x), на образующий полином P(x) степени (n-k). При этом умножение производится по обычным правилам алгебры с приведением подобных членов по модулю два. Следовательно, в случае отсутствия ошибок любая разрешенная кодовая комбинация циклического кода должна разделиться на образующий полином P(x) без остатка. Появление остатка от деления указывает на наличие ошибок в кодовой комбинации. При этом гарантийно обнаруживаются ошибки, определяемые выражениями (1.2) и (1.3). Кроме того, обнаруживается большая часть 
ошибок более высокой кратности.
Коды с постоянной четностью единиц
Наименьшей избыточностью обладают циклические (k+1,k)–коды, имеющие один проверочный единичный элемент и получившие название кодов с постоянной четностью единиц. Построение этих кодов осуществляется при помощи образующего полинома
|
Методами изложенными в (1.1). При этом разрешенные кодовые слова циклического (k+1,k)–кода во всех случаях содержит четное число единиц. Так как образующий полином является двучленом, то произведение G(x) P(x) независимо от числа членов первого сомножителя G(x) всегда будет содержать четное число членов.
Сущность метода состоит в том, что на передающей стороне в конце исходной комбинации G(x) k-элементного простого кода формируется дополнительный контрольный разряд, в который записывается 1, если число единиц в комбинации G(x) нечетное, и 0 – если число единиц четное.
Помехоустойчивость циклических кодов
Циклические коды можно использовать:
- для исправления ошибок;
- для обнаружения ошибок;
- для исправления и обнаружения ошибок.
Верность передаваемой информации
Наиболее предпочтительным является использование циклических кодов в режиме обнаружения ошибок, так как при этом достигается наибольшая верность передаваемой информации, определяемая по формуле
| (1.5) |
Использование циклических кодов для исправления ошибок приводит к снижению верности передаваемой информации, которая определяется по формуле (1.5), если исключить коэффициент 
и вместо параметра 
подставить параметр t, который определяет кратность гарантийно исправляемых циклическим кодом ошибок и связи с соотношением 
.
Режим одновременного исправления и обнаружения ошибок по достигаемой верности занимает промежуточное положение между рассмотренными режимами. Наиболее рациональными следует считать такие системы передачи дискретной информации, в которых циклические коды используются для обнаружения ошибок.
Потери информации
Потери информации имеют место в том случае, когда возникает ошибка, обнаруживаемая циклическим кодом, поэтому для обнаружения ошибок можно записать, что
| (1.6) |
где 
вероятность появления любой ошибки в кодовой комбинации.
Характеристика кодов с постоянной четностью единиц
Циклический (n, k)-код, построенный при помощи образующего полинома P(x) и не обладающий свойством постоянной четности единиц, может приобрести это свойство, если образующий полином P(x) домножить на двучлен (x+1) и формировать кодовые комбинации нового (n+1, k) – кода на основании полинома
| (1.7) |
В этом случае циклический (n+1, k) – код приобретает свойство дополнительно обнаруживать все ошибки нечетной кратности и, следовательно, для определения вероятности не обнаружения ошибок по выражению (1.5) необходимо увеличивать на единицу.
2 Алгоритмы расчета
Задаваемые для расчета технические параметры
Исходными данными для построения циклического кода являются:
- допустимое значение вероятности не обнаружения ошибок 
;
- число информационных единичных элементов первичного кода k;
- вероятность искажения единичного элемента кодовой комбинации 
, характеризующая качество канала связи.
Описание алгоритма
На рисунке 1 приведена структурная схема алгоритма нахождения образующего полинома циклического кода, удовлетворяющего заданной верности.
1 На первом этапе, используя выражение (1.1), определяем n*, удовлетворяющее следующему условию:
| (2.1) |
2 По заданному k и найденному значению n*(m) определим число проверочных единичных элементов
| (2.2) |
3 Уточняем число проверочных единичных элементов по таблице в приложении 1, выбирая ближайшее табличное значение 
4 Определяем табличное значение кратности гарантийно обнаруживаемых ошибок 
, соответствующее 
.
5 Так как табличные коды 
могут быть дополнены проверкой на четность, то определяем максимальную избыточность
и максимальную кратность гарантийно обнаруживаемых ошибок 
.
6 Уточняем длину кодовой комбинации циклического кода
.
Если n<n*(m), то будет иметь место так называемый укороченный циклический (n,k)- код, который по корректирующей способности эквивалентен полному циклическому 
-коду, число информационных единичных элементов которого больше на величину (n*-n).
7 Для найденных значений 
, используя выражение (1.5), определяем вероятность не обнаружения ошибок 
.
8 Проверяем логическое условие
9 При невыполнении условия (2.3) выбираем n*(m+1) и повторяем п. 2-8.
10 Если условие (2.3) выполняется, то методом перебора определяем минимальное число проверочных единичных элементов 
и соответствующие значения 
и 
, для которых выполняется условие (2.3).
11 Выбираем образующий полином P(x) по таблицам (приложение 1), соответствующий вычисленным значениям и
,
Рисунок 1. Структурная схема алгоритма нахождения образующего
полинома циклического кода
| (2.3) |
где 
- неприводимые многочлены, индекс 
которых возрастает с увеличением числа проверочных элементов ;
- индекс соответствующий .
При введении дополнительной проверки на четность
.
С целью сокращения записи все многочлены в приложении В указаны в восьмеричном представлении. При такой записи каждый символ обозначает три двоичных знака в соответствии со следующим кодом:
| 0<=>000 | 4<=>100 |
| 1<=>001 | 5<=>101 |
| 2<=>010 | 6<=>110 |
| 3<=>011 | 7<=>111. |
Коэффициенты многочленов в двоичной записи расположены в порядке убывания, так что коэффициент при слагаемом высшего порядка расположен слева. Например, число 45 в коде n* =31 обозначает многочлен 5-ой степени. В двоичной записи этому числу эквивалентно число
100 101
и соответствующий многочлен равен
.
Метод реализации алгоритма
Проблема реализации алгоритма заключается в динамическом перемещении по выполняемым этапам при выполнении или не выполнении логических условий. В данной работе эта проблема была устранена при помощи использования процедур, в каждой из которых выполнялись действия определенного этапа расчета алгоритма. И в логических блоках программы вызывается соответствующая процедура. Все основные переменные описаны как глобальные, т. е. каждой процедуре доступно свойство изменения переменных. Некоторые процедуры содержат рекурсивный вызов самих себя, при необходимости повторить все пройденные этапы, если появляется необходимость изменить начальные данные для выполнения логических условий.
3 Требование к программному изделию
Требование к функциональным характеристикам
Разработанная программа пригодна для нахождения образующего полинома для кодирования данных, а также граничных значений числа дополнительных единичных элементов и кратности обнаружения ошибок, при заданных параметрах, характеризующих качество каналов связи.
Контроль входной и выходной информации
Принимая входную информацию (исходные данные для расчетов) от пользователя, программа фильтрует входную информацию перед ее обработкой. При поступлении ошибочной информации или информации, неудовлетворяющей ограничительным критериям, становится невозможной обработка всего потока входной информации. В этом случае пользователю сообщается о некорректном вводе входной информации и предоставляется возможность повторного ввода.
4 Руководство пользователя
Интерфейс пользователя
На рисунке 2 показан внешний вид программы при запуске.
Рисунок 2. Внешний вид рабочего окна программы
Рабочее окно программы, как видно из рисунка, состоит из нескольких полей. В левой части окна пользователю предоставляется возможность изменить входные данные, которые установлены по умолчанию. Там же расположена кнопка «Теория по теме работы», с помощью этой кнопки можно просмотреть основную теорию. Между левым и правым полем рабочего окна расположена вертикальная кнопка, которая закрывает поле ввода начальных параметров и открывает таблицу с отчетом проделанных расчетов (рисунок 3). В правой части рабочего окна находится поле с вкладками: «Расчет полинома», на этой вкладке пользователь может последовательно выбирать этапы нахождения образующего полинома, а также сбросить в любое время все пройденные расчеты, возвратившись в начало; «Таблица ЦК» - здесь расположена таблица циклических кодов, по которым производится поиск полинома (рисунок 4). Пользователь может сохранить эту таблицу в файл Excel, для более подробного ознакомления с содержанием таблицы.
Рисунок 3. Вид окна с отчетом проделанной работы
Вкладка «Схема алгоритма» показывает окно с блок-схемой нахождения образующего полинома.
Вывод результатов
Вывод результатов осуществляется в поле рабочего окна программы «Отчет текущих действий», где динамически заполняются поля: «Этап», в котором записывается номер этапа при расчете полинома; «Действие», т. е. в нем отображается действие, которое было произведено для получения результата. Результаты каждого этапа заполняются в поле «Результат».
При выполнении всех этапов нахождения полинома, пользователь может сохранить таблицу с проделанной работой в файл Excel, для последующей печати на бумагу.
Рисунок 4. Таблица циклических кодов
5 Тестирование программы
Для тестирования разработанного программного продукта, введем значения вероятности допустимого значения не обнаружения ошибки, количество информационных разрядов и вероятность искажения единичного элемента. Возьмем для тестирования значения, введенные по умолчанию.
При выполнении всех этапов нахождения образующего полинома получаем таблицу 1 с отчетом проделанной работы.
В таблице приведены все полученные промежуточные значения, для нахождения образующего полинома.
Построим циклический код, удовлетворяющий исходным данным, вручную.
1 Определяем n*(m) из условия (2.1):
2 Находим число проверочных элементов
3 В приложении 1для n*(5)=31 выбираем ближайшее значение 
4 Определяем , соответствующее 
Таблица 1
| Этап: | Действие: | Результат |
| № 01 | Найти n*: | |
| При этом m: | ||
| № 02 | Определить r*: | |
| № 03 | Определить rt: | |
| И соответсв. gt: | ||
| № 04 | Определить rmax: | |
| Определить gmax: | ||
| № 05 | Уточнить n: | |
| № 06 | Определить Pno: | 2,2E-18 |
| № 07 | С проверкой на четность! | |
| rmin = | ||
| gmin = | ||
| nmin = | ||
| Ind соотв. rmin = | ||
| При этом Pno = | 1,9E-12 | |
| № 08 | Полином: | |
| X^6+X^5+X^3+X^2+X+1 |
5 Находим максимальную избыточность
и максимальную кратность гарантийно обнаруживаемых ошибок
6 Уточняем длину кодовой комбинации
7 Из выражения (1.5) для найденных значений 
определяем вероятность не обнаружения ошибок
8 Проверяем логическое условие (2.3):
9 Логическое условие выполняется, причем полученное значение значительно меньше допустимого. Затем последовательно подставляем три параметра из таблицы приложения 1, соответствующие найденному m, начиная с наименьших. Будем производить поиск до тех пор пока не найдем наименьшие параметры при которых выполняется условие (2.3). Такими являются первые элементы, соответствующему m из таблицы с проверкой на четность: 
10 В приложении 1 выбираем неприводимые многочлены 
Проверка на четность обеспечивается двучленом
Следовательно, образующий полином циклического (23,17)-кода будет иметь следующий вид:
Образующий полином 
является предпосылкой для построения кодирующего и декодирующего устройства циклического кода.
Заключение
При реальной передачи сигналов на дальние расстояния нет полной уверенности в том, что принимающая сторона весь сигнал примет без единой ошибки, это очевидно.
В данной работе были детально разобраны принципы образования кодовых комбинаций циклических кодов, алгоритм нахождения образующего полинома, при кодировании сигнала которым, обеспечивалась бы возможность нахождения ошибок при передаче данных по каналам связи с заданной характеристикой качества.
Также были разобраны все этапы нахождения образующего полинома для программной реализации. Особого внимания заслуживает алгоритм перемножения многочленов на последнем этапе образования образующего полинома.
Разработанная программа обеспечивает оптимизированный поиск образующего полинома, а также предоставляет гибкий характер работы пользователя с программным приложением по изменению параметров и просмотра промежуточных значений для конечного расчета.
Разработанное приложение может быть незаменимой частью более сложных программных пакетов для передачи данных на большие расстояния в сочетании с кодирующими и декодирующими приложениями или аппаратными реализациями этих устройств.
