Морфологический анализ – это метод исследования систем большой сложности, который был предложен в 1942 году швейцарским астрономом Ф.Цвикки. Слово «морфология» греческого происхождения, оно переводится как «учение о форме». Один из принципиальных аспектов данного метода – всеобщность, т.е. использование полной совокупности знаний об объекте; вследствие упора на полноту знаний необходимым требованием для морфологического анализа является полное отсутствие какого-либо предвзятого предварительного суждения.
Морфологический подход представляет собой упорядоченный способ рассмотрения предметов и получения систематизированной информации по всем возможным решениям изучаемой проблемы. Основная идея морфологического подхода – систематически находить наибольшее число, а в пределе – все возможные варианты решения поставленной проблемы или реализации системы путем комбинирования основных (выделенных исследователем) структурных элементов системы или их признаков. При этом система или проблема может разбиваться на части разными способами и рассматриваться в различных аспектах. Главная задача, которая решается при использовании данного метода, – ответить вопрос: как организовать поиск всех способов и методов решения данной конкретной проблемы?
Отправными точками морфологического исследования являются следующие пункты:
1) равный интерес ко всем объектам морфологического моделирования;
2) ликвидация всех ограничений и оценок до тех пор, пока не будет получена полная структура исследуемой области;
3) максимально точная формулировка поставленной проблемы.
Морфологический анализ включает целый ряд приемов, но принцип у них один: систематизированное рассмотрение явлений, предметов, стремление не пропустить ни одной возможности, ничего не отбрасывая без предварительного исчерпывающего исследования. Этой цели служит прием систематизированного охвата, при котором исследование начинают с данного уровня знаний. Затем систематически просматривают одну за другой все возможные области знаний, пока не достигнут другого уровня знаний.
В процессе анализа все объекты разбиваются на группы, каждая из которых подвергается тщательному изучению. Такой подход позволяет систематизированно накапливать данные для последующих исследований и организовывать проверку их на формальную полноту.
Для удобства представления данных используют так называемый «морфологический ящик». Он является многомерным пространством. «Морфологический ящик» строится в виде дерева решения или таблицы (матрицы) решения, в клетках которых помещены соответствующие параметры. Последовательное соединение одного какого-либо параметра первого уровня с одним из параметров последующих уровней представляет собой одно из возможных решений проблемы. Учитывая, что некоторые из этих решений практически неосуществимы, действительное число решений будет несколько меньше.
Если предложенная проблема полностью решена, то каждое отделение этого «ящика» будет содержать только одно возможное решение или вообще не будет его иметь. Появление двух или более решений в одном отделении указывает, что не все параметры были учтены или введены в систему. Поэтому производится поиск упущенных параметров. Именно это свойство делает морфологический анализ проектных решений ценным инструментом применительно к исследованию тех или иных социальных проблем, перспективности и возможного исхода проектных разработок в социальной сфере.
Таким образом, с помощью морфологического анализа удается получить качественно новое проектное решение. Преимущества данного метода в том, что он осуществим при наличии малого количества информации по изучаемой проблеме, а для оценки решений можно использовать самые общие критерии.
Процедуры морфологического анализа проектных решений состоит из следующих этапов.
1. Предварительный анализ. Осуществляется точная формулировка проблемы, подлежащей решению. Лицо, принимающее решение (ЛПР), выбирает, какое проектное решение ему следует принять применительно к рассматриваемой конкретной проблеме. Производится тщательный анализ всех параметров, важных с точки зрения решения данной проблемы. При этом осуществляется выбор критериев оценки проектного решения, которые тесно связаны с последствиями решений. В итоге сама проблема определена, известны возможные альтернативы действий и критерии их оценки.
2. Структурный анализ. ЛПР проводит качественную структуризацию проблемы, в ходе которого осуществляется построение «морфологического ящика», потенциально содержащего все решения. В ходе такого упорядоченного анализа возможно не только полностью охарактеризовать заданный объект некоторого класса, но и установить перечень характеристик, которые будут оставаться в силе для любого объекта того же класса. На основе такого набора общих характеристик можно путем перестановок и различных сочетаний выработать вероятностные характеристики объектов, которые еще не существуют, но могут существовать.
3. Анализ неопределенности. ЛПР устанавливает определенные значения вероятности для тех ветвей, которые начинаются в вершинах-случаях. Это осуществляется с помощью совокупности методов и процедур, основанных на прошлых эмпирических данных, на допущениях и результатах различных аналитических и имитационных моделей, на мнениях экспертов, а также на субъективных суждениях ЛПР.
4. Анализ полезности (ценности). Следующим этапом является установление ЛПР численных значений полезности последствий, связанных с реализацией того или иного пути на «дереве решений», т.е. изучение всех полученных решений с точки зрения их функциональной ценности. Для этого устанавливается шкала оценок. О характеристиках можно судить, только исходя из каких-то желаемых целей. При поставленных целях ценность различных решений представляется графически в форме так называемых топологических характеристических карт. Это наиболее сложный момент морфологического анализа. Универсальной формулы для определения функциональной ценности различных решений нет. В каждой конкретной задаче с любым путем будут связаны различные экономические и прочие затраты и приобретения, существенные с точки зрения ЛПР и других заинтересованных лиц.
5. Выбор проектных решений. На последнем этапе оптимальная альтернатива может быть найдена с помощью вычислений — оптимальной будет та стратегия, которая максимизирует ожидаемую полезность. Эта стратегия указывает, как должно действовать ЛПР в каждой вершине «дерева решений». Когда последствие детерминировано и одномерно, то в концептуальном плане проблема ясна: нужно выбрать ту из возможных альтернатив, которая максимизирует или минимизирует значение используемой целевой функции. Конечно, задача оптимизации может оказаться достаточно сложной, но эти сложности носят технический, а не концептуальный характер.
Таким образом, в результате этого метода создается новая информация об изучаемом объекте и вырабатывается оценка всех возможных альтернатив для каждой составной части проблемы. Тем самым достигается цель морфологического анализа – выработка наиболее приемлемого решения на основе рассмотрения каждого возможного решения.
Одной из форм представления «морфологического ящика» является «дерево решений». Термин «дерево» подразумевает использование иерархической структуры, полученной путем разделения обшей цели на подцели, а их, в свою очередь, на более детальные составляющие, которые можно называть подцелями нижележащих уровней или, начиная с некоторого уровня, – функциями. Как правило, данный метод используется для иерархических структур, имеющих отношения строго древовидного порядка, но сам метод иногда применяется и в случае «слабых» иерархий. Отметим, что при использовании данного метода в качестве средства целеполагания вводят термин «дерево целей». При его применении для раскрытия и уточнения функций управления говорят о «дереве функций». При структуризации тематики научно-исследовательской организации удобнее пользоваться термином «дерево проблемы».
 Принцип ветвления вариантов проектных решений должен быть понятен из рисунка 29. С помощью «дерева решений» сложное проектное решение иерархически расчленяется на элементарные уровни, причем эти решения становятся все более конкретными по мере того, как ветвление опускается на более низкие уровни. Такая форма дает больше свободы представления, чем блок-схема программ, поскольку на уровнях единичных решений допустимы не только два, но большое число исходов (ветвлений).
Принцип ветвления вариантов проектных решений должен быть понятен из рисунка 29. С помощью «дерева решений» сложное проектное решение иерархически расчленяется на элементарные уровни, причем эти решения становятся все более конкретными по мере того, как ветвление опускается на более низкие уровни. Такая форма дает больше свободы представления, чем блок-схема программ, поскольку на уровнях единичных решений допустимы не только два, но большое число исходов (ветвлений).
Рис. 29. «Дерево решений»
«Дерево решений» дает отличный обзор всего поля проектных решений и обеспечивает проверку его полноты. Существует столько вариантов решений, сколько ветвей в «дереве». Основной вопрос состоит в том, чтобы получить такой отличный обзор, если, конечно, поле решений может быть вообще представлено подобным образом. При этом всю совокупность затрат и приобретений, которые возникнут при реализации некоторой ветви, будем называть последствием, связанным с этой ветвью.
В этом случае надо построить цепочку проектных решений, в которой переход на более низкий уровень должен сопровождаться большей конкретизацией. Следовательно, в перечне беспорядочно собранных вариантов решений уже неявно заключена некоторая иерархическая система, которую необходимо отобразить в «дереве решений». В беспорядочном наборе проектных решений необходимо обнаружить общие черты, на основе которых образовать группы (классы) проектов.
Процесс, при котором отдельные решения сначала собираются, а затем группируются, можно рекомендовать в том случае, если нет еще никаких представлений о ветвлениях будущего «дерева решений». В том же случае, если заранее известно, как можно дифференцировать грубые предварительные решения и разложить их на единичные, стоит начинать с построения «дерева решений», чтобы потом с его помощью найти сами единичные решения.
При построении дерева решения может оказаться целесообразным использование следующих уровней: уровень A – цель решения; уровень B – стратегия решения; уровень C – классы (группы) методов решения; уровень D – методы; уровень E – конкретные варианты.
При таком подходе единичные варианты на каждом иерархическом уровне в зависимости от решаемой проблемы можно сопоставлять друг с другом с использованием определенных критериев, которые при переходе на другой уровень могут изменяться.
Рассмотрим другую форму представления «морфологического ящика» – таблицу решений, которая позволяет провести проверку возможных вариантов решений на их полноту. Данный метод предполагает, что существует некоторое число так называемых «опорных пунктов» знания в любой исследуемой области. Исходя из ограниченного числа опорных пунктов знания и достаточного числа принципов мышлений ищут все возможные решения поставленной проблемы. Например, если предпринять систематический анализ: попробовать упорядочить и классифицировать разнородные проектные решения субъекту, то можно получить определенное табличное представления проектов. Например, при принятии решения о создании реабилитационного центра можно выделить следующие три базовых объекта: место расположения, срок реализации проекта и строительную организацию (табл. 37). В этом случае каждая клетка в таблице 37 относится к возможным вариантам, рассмотренным относительно основных объектов и узловых проблем проектного решения.
Таблица 37
«Таблица решений» для проекта создания
реабилитационного центра.
| Основные объекты и узловые проблемы | Основные характеристики вариантов | |||
| Место |  В центре В центре
| На периферии | За городом | Под землей |
| Сроки реализации проекта (мес.) | 0 – 1,5 | 1,5-12 | 12 – 24 | Более 24 |
| Строительная организация | ООО «Строй» | ОАО «Сервисстрой» | МУП «Город сервис«дерева решений» |
Такое табличное представление позволяет увидеть необычные варианты проектного решения. Например, в данном проекте можно попробовать обсудить вариант создания реабилитационного центра на базе существующих подземных площадей, принадлежащих МУП «Город сервис», что позволяет сократить сроки реализации проекта до минимума.
Задание 3. Используя морфологический ящик в форме дерева решений осуществить выбор лучшего проекта встречи Нового года для детей детского дома.
Решение
1. Составление «дерева решений» (рис. 30).
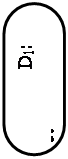
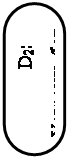

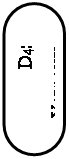



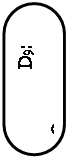


Рис. 30. «Дерево решений» для выбора лучшего проекта
встречи Нового года детьми детского дома
2. Выбор критериев и оценка их значимости. В данном случае в качестве критериев будут выступать следующие параметры: денежные расходы (m); ожидаемые впечатления (p); временные затраты (t). При этом обратим внимание, что для параметров «денежные расходы» (m) и «временные затраты» (t) меньшие значения соответствуют лучшим вариантам, а для параметра «ожидаемые впечатления» (p) – большие значения соответствуют лучшим вариантам. Метод не позволяет работать с разнонаправленными критериями, поэтому для параметра «ожидаемые впечатления» (p) примем обратную шкалу: меньшие баллы соответствуют лучшим вариантам. Таким образом, задача, которую предстоит решить – это задача на нахождение минимальных значений.
Проведем оценку значимости этих критериев. Допустим, что наиболее значимым критерием для нас является уровень ожидаемых впечатлений – он значимее остальных в 3 раза. Отсюда, решая уравнение km +3 kp+ kt= 1, получаем весовые коэффициенты для критериев: km = 0,2; kp =0,6; kt = 0,2.
3.Оценка показателей. В таблице 38 даны оценки денежных расходов; ожидаемых впечатлений и временных затрат для каждого варианта встречи Нового года детьми детского дома.
Таблица 38
Оценка параметров вариантов встречи Нового года воспитанниками детского дома
| Денежные расходы, m, тыс.руб. | ||||||||||||||||||||||
| mD | mD1=22 | mD2=30 | mD3=10 | mD4=2 | mD5=25 | mD6=15 | mD7=110 | mD8=80 | mD9=50 | |||||||||||||
| mC | mC1=26 | mC2=6 | mC3=20 | mC4=80 | ||||||||||||||||||
| mB | mВ1=16 | mВ2=50 | ||||||||||||||||||||
| mА | mА1=33 | |||||||||||||||||||||
| Ожидаемые впечатления, p, балл | ||||||||||||||||||||||
| pD | pD1=2 | pD2=1 | pD3=3 | pD4=4 | pD5=1 | pD6=2 | pD7=1 | pD8=1,3 | pD9=1,6 | |||||||||||||
| pC | pC1=1,5 | pC2=3,5 | pC3=1,5 | pC4=1,3 | ||||||||||||||||||
| pB | pВ1=2,5 | pВ2=1,4 | ||||||||||||||||||||
| p | pА1=1,95 | |||||||||||||||||||||
| Временные затраты, t, дни | ||||||||||||||||||||||
| tD | tD1=5 | tD2=7 | tD3=3 | tD4=1 | tD5=6 | tD6=6 | tD7=14 | tD8=11 | tD9=8 | |||||||||||||
| tC | tC1=6 | tC2=2 | tC3=6 | tC4=11 | ||||||||||||||||||
| tB | tВ1=4 | tВ2=8,5 | ||||||||||||||||||||
| tА | tА1=6,25 | |||||||||||||||||||||
Оценка показателей (mD, pD, tD) конкретных вариантов встречи Нового года детьми детдома (уровень «D») проводится на основе имеющегося опыта или экспертно. Оценка на следующих уровнях проводится как усредненное значение предыдущих уровней.
2. Расчет коэффициентов предпочтения. Данный расчет представлен ниже (табл. 39).
Таблица 39
Расчет коэффициентов предпочтения для различных вариантов встречи Нового года воспитанниками детского дома
Денежные расходы,  , тыс.руб. , тыс.руб.
| km =0,2 | 0,048 | 0,152 | |||||||
Ожидаемые впечатления,  , балл , балл
| kp =0,6 | 0,385 | 0,215 | |||||||
Временные затраты,  , дни , дни
| kt = 0,2 | 0,064 | 0,136 | |||||||
| Коэффициент предпочтения уровня А, KВ | 0,497 | 0,503 | ||||||||
Денежные расходы,  , тыс.руб. , тыс.руб.
| km =0,2 | 0,163 | 0,038 | 0,040 | 0,160 | |||||
Ожидаемые впечатления,  , балл , балл
| kp =0,6 | 0,180 | 0,420 | 0,321 | 0,279 | |||||
Временные затраты,  , дни , дни
| kt = 0,2 | 0,150 | 0,050 | 0,071 | 0,129 | |||||
| Коэффициент предпочтения уровня B, КС | 0,493 | 0,508 | 0,432 | 0,568 | ||||||
Денежные расходы,  , тыс.руб. , тыс.руб.
| km =0,2 | 0,085 | 0,115 | 0,167 | 0,033 | 0,125 | 0,075 | 0,092 | 0,067 | 0,042 |
Ожидаемые впечатления,  , балл , балл
| kp =0,6 | 0,400 | 0,200 | 0,257 | 0,343 | 0,200 | 0,400 | 0,154 | 0,200 | 0,246 |
Временные затраты, 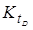 , дни , дни
| kt = 0,2 | 0,083 | 0,117 | 0,150 | 0,050 | 0,100 | 0,100 | 0,085 | 0,067 | 0,048 |
| Коэффициент предпочтения уровня C, КD, | 0,568 | 0,432 | 0,574 | 0,426 | 0,425 | 0,575 | 0,330 | 0,333 | 0,336 |
Расчет коэффициентов предпочтения для уровня «В» осуществляется по следующим формулам:
 , (7.10)
, (7.10)
 , (7.11)
, (7.11)
 , (7.12)
, (7.12)
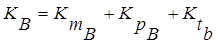 . (7.13)
. (7.13)
mВi, pВi, tВi – соответствующие значения денежных расходов, ожидаемых впечатлений, временных затрат для i-того варианта уровня В;
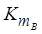 ,
,  ,
,  – соответствующие коэффициенты предпочтения для каждого из анализируемых показателей для i-того варианта уровня В;
– соответствующие коэффициенты предпочтения для каждого из анализируемых показателей для i-того варианта уровня В;
KB – суммарный коэффициент предпочтения для i-того варианта уровня В.
 ,
,  ,
,  ,
, 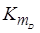 ,
,  ,
,  , а также KС и KD рассчитываются аналогично. Результаты их расчета представлены в таблице 39.
, а также KС и KD рассчитываются аналогично. Результаты их расчета представлены в таблице 39.
3. Выбор оптимального варианта. В данном случае рассчитывается интегральный показатель (Ri) для каждого конкретного i- тоговарианта по следующей формуле:
 , (7.13)
, (7.13)
где N – количество уровней «дерева решений»;
Kj – коэффициент предпочтения i- тоговарианта соответствующего уровня.







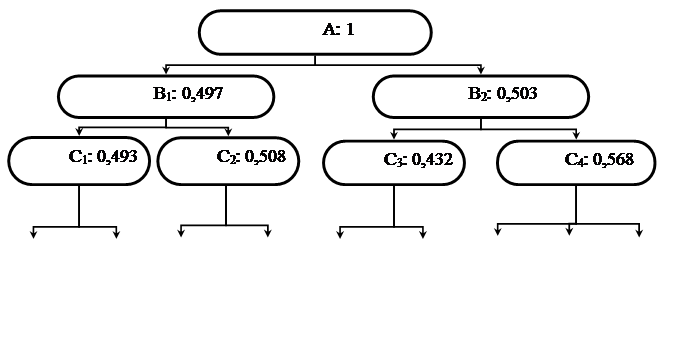
| 0,139 | 0,106 | 0,145 | 0,108 | 0,092 | 0,125 | 0,094 | 0,095 | 0,096 |
Рис. 31. Выбор проектных решений встречи Нового года детьми
детского дома на основе минимизации значения целевой функции
Таким образом, в данном случае, поскольку решали задачу на нахождение минимальных значений, а минимальное значение соответствует варианту D5 , то наилучшим вариантом проектного решения будет вариант вечеринки в кафе. В этом случае воспитанники дома получать максимальные впечатления с одновременной относительной минимизацией временных и материальных затрат.






