МАТЕМАТИЧЕСКАЯ ОБРАБОТКА ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ
(Методические указания к лабораторной работе)
ЗАДАНИЕ. Приведены результаты 50 наблюдений безотказной работы партии электрических лампочек(в час. работы):
I. Первичная обработка результатов наблюдений.
1). Выполним группировку данной выборки случайной величины (кратко: СВ X), т.е. разобьем наблюдаемые значения СВ на к частичных интервалов равной длины h и подсчитаем частоты  попадания СВ в частичные интервалы.
попадания СВ в частичные интервалы.
Просматривая приведённые значения, находим:
 ,
, 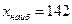 .
.
Длину интервала h можно выбирать различными приемами. Одним из удобных при определении h является способ, предложенный Стерджесом:  .
.
Здесь n - объём выборки, в нашем задании n = 50. Тогда 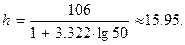
За h удобнее взять ближайшее целое число: h = 16.
2). За начало 1-го интервала рекомендуется принять величину 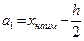 ,
,
т.е. 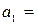 36 - 8 = 28. Тогда
36 - 8 = 28. Тогда 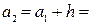 28 + 16 = 44,
28 + 16 = 44,
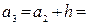 44 + 16 = 60,
44 + 16 = 60,  = 76,
= 76,  = 92,
= 92, 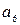 = 108,
= 108, 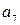 = 124,
= 124, 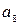 = 140,
= 140, 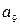 = 156.
= 156.
Шкала интервалов и группировка исходных статистических данных сведены в таблицу 1, причем в каждый интервал включены те значения вариант 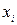 , которые удовлетворяют неравенству
, которые удовлетворяют неравенству 
Таблица 1
Интервалы 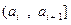
| Подсчет частот | Частоты 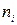
| Относительная частота 
|
| (28; 44 ] (44; 60 ] (60; 76 ] (76; 92 ] (92; 108 ] (108; 124 ] (124; 140 ] (140; 156 ] | * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * | 0,04 0,06 0,14 0,16 0,30 0,18 0,08 0,04 | |
| К = 8 | Сумма: | 1,00 |
3). Построим дискретный статистический ряд, найдя середины частичных интервалов по формуле  . Результаты запишем в таблице 2.
. Результаты запишем в таблице 2.
Таблица 2
| Интервалы | Середины 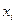
| Частота 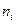
| Относит. Частота 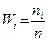
| Плотность относительной частоты
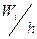
|
| (28; 44 ] (44; 60 ] (60; 76 ] (76; 92 ] (92; 108 ] (108; 124 ] (124; 140 ] (140; 156 ] | 0,04 0,06 0,14 0,16 0,30 0,18 0,08 0,04 | 0,00250 0,00375 0,00875 0,01000 0,01875 0,01125 0,00500 0,00250 | ||
| Сумма: | 1,00 |
По данным табл. 2 строим гистограмму. На оси абсцисс откладываем частичные интервалы, на каждом из них строим прямоугольник, площадь которого равна относительной частоте 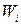 (для этого за высоту прямоугольника нужно взять плотность относительной частоты). Площадь всех прямоугольников будет равна единице.
(для этого за высоту прямоугольника нужно взять плотность относительной частоты). Площадь всех прямоугольников будет равна единице.
Если построена гистограмма интервального распределения, то полигон того же распределения получим, если соединим прямолинейными отрезками середины верхних оснований прямоугольников.
 |

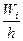



 0,02
0,02
 | |||
 | |||


 0,01
0,01
 |








 0 28 44 60 76 92 108 124 140 156
0 28 44 60 76 92 108 124 140 156 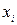
Рис. 1
II. Построение выборочной (эмпирической) функции распределения.
Эмпирическая функция распределения 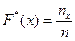 , где
, где  - число выборочных значений меньших
- число выборочных значений меньших 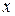 , n - объём выборки.
, n - объём выборки.
Полученный результат записывают так:
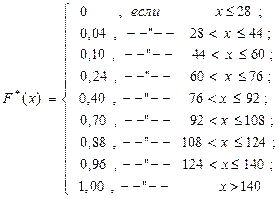
 |
F*(x)













 1
1
 | |||
 |

 0,5
0,5
 | |||||
 | |||||
 |
0 28 44 60 76 92 108 124 140 156
 Рис. 2
Рис. 2
III. Вычисление числовых характеристик
Под числовыми характеристиками выборки СВ Х понимают:
выборочную среднюю 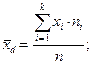
выборочную дисперсию 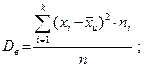
выборочное среднее квадратическое отклонение 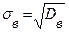 ;
;
исправленную дисперсию 
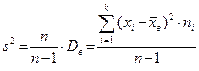 ;
;
исправленное среднее квадратическое отклонение 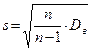 .
.
Вычисления выборочной средней 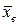 и выборочной дисперсии
и выборочной дисперсии 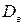 удобнее провести, используя таблицу 4.
удобнее провести, используя таблицу 4.
Таблица 4 
Середины
Интервалов 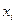
| Частоты

|
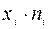
|
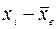
|
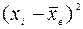
|
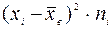
|
| -58,88 -42,88 -26,88 -10,88 5,12 21,12 37,12 53,12 | 3466,85 1838,69 722,53 118,37 26,21 446,05 1377,89 2821,73 | 6933,71 5516,08 5057,74 947,00 393,22 4014,49 5511,58 5643,47 | |||
| Сумма: | 34017,28 |
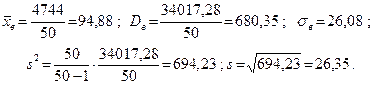
IV. Выбор закона распределения.
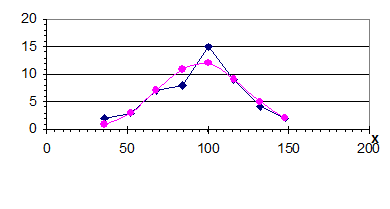
Построенные полигон и гистограмма относительных частот (рис. 1) напоминают нормальную кривую (кривую Гаусса). Поэтому есть основания предположить, что изучаемая СВ Х распределена по нормальному закону. Но эту гипотезу надлежит проверить.
В этих целях вычисляют теоретические частоты (выравнивающие частоты) и по ним строят кривую.
Первый способ. Один из способов построения нормальной кривой по данным наблюдений состоит в следующем:
1). Находят  и
и 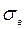 ;
;
2). Определяют ординаты 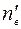 (выравнивающие частоты) по формуле
(выравнивающие частоты) по формуле  ,где n - объём выборки;
,где n - объём выборки;
h - шаг (длина частичного интервала);
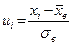 ,
, 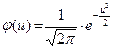 - нормированная плотность нормального распределения (В.Е.Гмурман, приложение 1).
- нормированная плотность нормального распределения (В.Е.Гмурман, приложение 1).
В нашем случае 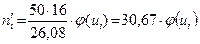 .
.
Вычисления проведены в таблице 6.
Таблица 6
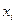
| 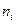
| 
| 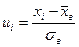
| 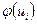
| 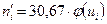
| |
| -58,88 -42,88 -26,88 -10,88 5,12 21,12 37,12 53,12 | -2,26 -1,64 -1,03 -0,42 0,20 0,81 1,42 2,04 | 0,0310 0,1040 0,2347 0,3652 0,3910 0,2874 0,1456 0,0498 | 0,95 3,20 7,20 11,20 11,99 8,81 4,57 1,53 | |||
 |
Замечание. В последнем столбце таблицы указаны теоретические частоты, которые получаются округлением до ближайшего целого числа предыдущих значений.
 Рис.3
Рис.3
На рис. 3 построена нормальная (теоретическая) кривая по выравнивающим частотам 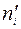 и полигон наблюдаемых частот. Сравнение графиков наглядно показывает, что построенная теоретическая кривая нормального распределения удовлетворительно отражает данные наблюдений.
и полигон наблюдаемых частот. Сравнение графиков наглядно показывает, что построенная теоретическая кривая нормального распределения удовлетворительно отражает данные наблюдений.
Второй способ ( с использованием функции Лапласа).
1). Находят 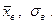
2). Составляют новые интервалы 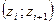 , концы которых вычисляют по формулам:
, концы которых вычисляют по формулам: 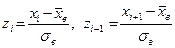 , причем наименьшее значение
, причем наименьшее значение  полагают равным
полагают равным  , а наибольшее значение
, а наибольшее значение 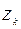 полагают равным
полагают равным  .
.
3). Вычисляют теоретическую вероятность 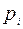 попадания случайной величины Х в интервал
попадания случайной величины Х в интервал 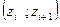 по равенству
по равенству 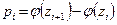 , где
, где 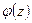 - функция Лапласа (см. В.Е.Гмурман, приложение 2).
- функция Лапласа (см. В.Е.Гмурман, приложение 2).
4). Теоретические частоты находят по формуле 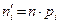 , где n – объём выборки.
, где n – объём выборки.
Непосредственные вычисления проведём в таблицах 7, 8.
В таблице 7 найдём интервалы 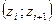 .
.
Таблица 7
| Границы частичных интервалов | Частоты 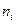 
| 
| 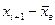
| 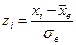
| 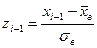
| |
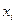
| 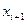
| |||||
| -66,88 -50,88 -34,88 -18,88 -2,88 13,12 29,12 45,12 | -50,88 -34,88 -18,88 -2,88 13,12 29,12 45,12 61,12 |
- 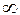 -1,95
-1,34
-0,72
-0,11
0,50
1,12
1,73
-1,95
-1,34
-0,72
-0,11
0,50
1,12
1,73
|
-1,95
-1,34
-0,72
-0,11
0,50
1,12
1,73
+ 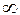
|
В таблице 8 найдены теоретические вероятности 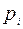 и по ним - теоретические частоты
и по ним - теоретические частоты 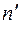 .Получены те же результаты, что и при первом способе (см. табл. 6).
.Получены те же результаты, что и при первом способе (см. табл. 6).
Таблица 8
| Границы интервала | 
| 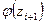
| 
| 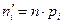
| Исправленное 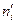
| |
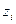
| 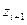
| |||||
- 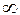 -1,95
-1,34
-0,72
-0,11
0,50
1,12
1,73
-1,95
-1,34
-0,72
-0,11
0,50
1,12
1,73
|
-1,95
-1,34
-0,72
-0,11
0,50
1,12
1,73
+ 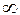
| -0,5000 -0,4744 -0,4099 -0,2642 -0,0438 0,1915 0,3686 0,4582 | -0,4744 -0,4099 -0,2642 -0,0438 0,1915 0,3686 0,4582 0,5000 | 0,0256 0,0645 0,1457 0,2204 0,2353 0,1771 0,0896 0,0418 | 1,28 3,23 7,29 11,02 11,77 8,86 4,48 2,09 | 4+1 |
| 1,0000 | 49+1=50 |
V. Обоснование гипотезы о предполагаемом законе распределения.
По виду полигона и гистограммы (рис.1) было сделано предположение, что СВ Х подчинена нормальному закону. Из этого предположения удалось вычислить теоретические частоты 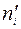 и построить теоретическую кривую нормального распределения, что ещё более подтверждает, что генеральная совокупность СВ Х подчинена нормальному закону.
и построить теоретическую кривую нормального распределения, что ещё более подтверждает, что генеральная совокупность СВ Х подчинена нормальному закону.
Однако высказанную гипотезу (называют её нулевой 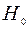 ) необходимо подтвердить, т.е. требуется проверить согласованность имеющегося эмпирического материала с предполагаемым теоретическим распределением случайной величины в генеральной совокупности.
) необходимо подтвердить, т.е. требуется проверить согласованность имеющегося эмпирического материала с предполагаемым теоретическим распределением случайной величины в генеральной совокупности.
Проверка осуществляется с помощью специально подобранной случайной величины – критерия согласия.
Применим критерий согласия  - «хи квадрат» (критерий Пирсона). С этой целью будем сравнивать эмпирические (наблюдаемые) частоты
- «хи квадрат» (критерий Пирсона). С этой целью будем сравнивать эмпирические (наблюдаемые) частоты  и теоретические частоты
и теоретические частоты 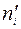 по формуле
по формуле 
Составим расчетную таблицу 9.
По таблице критических точек распределения 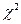 (Гмурман В.Е., приложение 5) по заданному уровню значимости
(Гмурман В.Е., приложение 5) по заданному уровню значимости 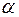 и числу степеней свободы
и числу степеней свободы 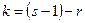 , где s – число частичных интервалов, r - число параметров предполагаемого распределения СВ Х, найдём критическое значение
, где s – число частичных интервалов, r - число параметров предполагаемого распределения СВ Х, найдём критическое значение  .
.
Таблица 9
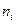
| 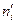
| 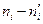
| 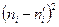
| 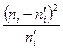
| Расчет для контроля | |

| 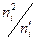 
| |||||
| -3 -1 | 0,82 0,75 0,2 | 4,00 3,00 7,00 5,82 18,75 9,00 3,20 2,00 | ||||
| 2,77 | 52,77 |
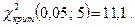 |
В нашем случае число степеней свободы
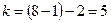 , а уровень значимости a = 0,05 (по заданию). По приложению 5 находим:
, а уровень значимости a = 0,05 (по заданию). По приложению 5 находим:
В таблице 9 найдено: 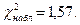
Так как 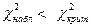 , то нет оснований для отклонения гипотезы о нормальном распределении генеральной совокупности СВ Х.
, то нет оснований для отклонения гипотезы о нормальном распределении генеральной совокупности СВ Х.
Для контроля вычислений формулу (2) преобразуют к виду 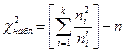 ; имеем:
; имеем: 






