оллекторы представл€ют собой трубопроводы с переменным по длине расходом. ѕотери напора в таком коллекторе складываютс€ из потерь напора на трение на каждом участке:
 /39/
/39/
где n - число участков длиной li; hi - потери напора на трение на i -м участке коллектора.
Ќефтебазовые коллекторы имеют посто€нный диаметр с отбором нефтепродукта через равные промежутки длиной l, определ€емые рассто€нием между сливно-наливными сто€ками.
ƒл€ удобства расчета коллектора потери напора hi лучше вычисл€ть по формуле Ћейбензона:
 /40/
/40/
“огда потери напора в коллекторе можно записать следующим образом:
 /41/
/41/
где q - расход нефтепродукта в одном сливно-наливном сто€ке.
ѕрин€в qn= Q, т.е. максимальному расходу нефтепродукта в коллекторе, anl= L, т.е. расчетной длине коллектора, можем записать:
 /42/
/42/
¬ыражение в скобках показывает, во сколько раз потери напора в коллекторе с переменным расходом меньше потерь напора в трубопроводе той же длины с посто€нным расходом Q.
»сследуем полученное уравнение /42/ дл€ различных режимов течени€.
ѕри ламинарном режиме 
 /43/
/43/
ѕоскольку  , то
, то
 /44/
/44/
“.е. в коллекторах с переменным расходом при ламинарном режиме потери напора на трение примерно равны 1/2 гидравлического сопротивлени€ трубопровода той же длины с посто€нным расходом.
ѕри развитом турбулентном режиме течени€ (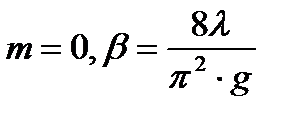 )
)
 /45/
/45/
ѕоскольку  , то
, то
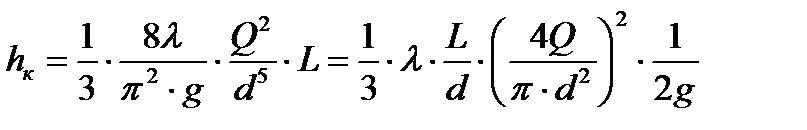 /46/
/46/
“.е. при развитом турбулентном режиме потери напора на трение в коллекторе с переменным расходом в 3 раза меньше потерь напора в трубопроводе с посто€нным расходом.
“ехнологический расчет самотечных трубопроводов
–асчет самотечных трубопроводов заключаетс€ в определении их диаметра (или размеров коллектора, если он имеет не круглую форму), уклона и параметров их работы Ц наполнени€ и скорости. ќбычно предварительно определ€етс€ расход, который €вл€етс€ исходным дл€ расчета. –асчет трубопроводов Ц не только гидравлическа€ задача. ѕолученные результаты должны удовлетвор€ть технологическим и экономическим требовани€м, о которых будет сказано ниже.
¬ цел€х упрощени€ гидравлических расчетов водоотвод€щих сетей движение воды в них условно принимаетс€ установившимс€ и равномерным. ѕо поводу расчета самотечных трубопроводов существует две точки зрени€.
ѕерва€ точка зрени€. ƒл€ расчета рекомендуютс€ формулы посто€нства расхода
 (2.1.)
(2.1.)
и Ўези
 (2.2.)
(2.2.)
где qЦ расчетный расход;  Ц площадь живого сечени€; v Ц скорость; C Ц коэффициент Ўези;
Ц площадь живого сечени€; v Ц скорость; C Ц коэффициент Ўези;

RЦ гидравлический радиус;  Ц смоченный периметр; iЦ уклон лотка (i=hl/l), hlЦ падение лотка на длине l.
Ц смоченный периметр; iЦ уклон лотка (i=hl/l), hlЦ падение лотка на длине l.
¬ формуле (2.2) прин€то, что гидравлический уклон I равен уклону лотка i, так как движение воды равномерное, при котором глубины потока и средние скорости в сечени€х 1-1 и 2-2 равны.
ƒл€ определени€ коэффициента Ўези рекомендуетс€ формула Ќ. Ќ. ѕавловского (при 0,1 < R < 3 м)
 (2.3)
(2.3)
где y Ц показатель степени, определ€емый по формуле
 (2.4)
(2.4)
где n - коэффициент шероховатости, завис€щий от состо€ни€ стенок трубопровода (табл. 2.1).
|
|
|
ƒл€ приблизительных расчетов Ќ.Ќ. ѕавловский рекомендовал следующие формулы:
 при
при 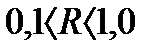
 при
при 
ѕри у = 1/6 формула (2.3) известна как формула ћаннинга. ‘ормула (2.3) справедлива дл€ области турбулентного режима течени€ жидкости.
“аблица 2.1

¬тора€ точка зрени€. ƒл€ расчета рекомендуютс€ формулы (2.1) и ƒарси:
 (2.6)
(2.6)
ѕроф. Ќ.‘. ‘едоров рекомендует определ€ть коэффициент  гидравлического трени€ по формуле
гидравлического трени€ по формуле
 (2.7)
(2.7)
где  Ц эквивалентна€ абсолютна€ шероховатость; а2Ц коэффициент, учитывающий характер шероховатости стенок труб (табл. 2,1);
Ц эквивалентна€ абсолютна€ шероховатость; а2Ц коэффициент, учитывающий характер шероховатости стенок труб (табл. 2,1); 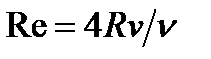 Ц число –ейнольдса; vЦ кинематический коэффициент в€зкости.
Ц число –ейнольдса; vЦ кинематический коэффициент в€зкости.
≈сли учесть соотношение

то формула (2.6) преобразуетс€ в формулу (2.2). ¬ этой части расхождени€ в двух точках зрени€ отсутствуют.
ѕо формуле (2.7) коэффициент  (следовательно, и коэффициент C) завис€т не только от относительной шероховатости, но и от числа –ейнольдса. Ёта формула справедлива дл€ всех трех областей турбулентного режима движени€ жидкости: областей гладкого, вполне шероховатого трени€ и переходной области между ними. »сследовани€ показали, что трубопроводы водоотвод€щих сетей работают в области вполне шероховатого трени€. ƒл€ возможных условий проектировани€ расчеты но формулам (2.1) Ц (2.3) и (2.6) Ц (2.7) дают практически одинаковые результаты.
(следовательно, и коэффициент C) завис€т не только от относительной шероховатости, но и от числа –ейнольдса. Ёта формула справедлива дл€ всех трех областей турбулентного режима движени€ жидкости: областей гладкого, вполне шероховатого трени€ и переходной области между ними. »сследовани€ показали, что трубопроводы водоотвод€щих сетей работают в области вполне шероховатого трени€. ƒл€ возможных условий проектировани€ расчеты но формулам (2.1) Ц (2.3) и (2.6) Ц (2.7) дают практически одинаковые результаты.
ѕри определении местных потерь напора используетс€ формула ¬ейсбаха:
 (2.8)
(2.8)
где  Ц коэффициент местного сопротивлени€, значени€ которого привод€тс€ в справочной литературе.
Ц коэффициент местного сопротивлени€, значени€ которого привод€тс€ в справочной литературе.
»звестно, что максимальный расход воды в трубах наблюдаетс€ при наполнении h/d= 0,95. ѕоэтому наполнение, большее этого значени€, принимать нецелесообразно. ќднако, расчетные наполнени€ рекомендуетс€ принимать даже меньше этого значени€ по следующим двум причинам. ¬о-первых, при определении расчетных расходов не учитываетс€ колебание расходов в пределах часа суток, когда может наблюдатьс€ максимальный расход. ј это колебание может быть и в меньшую, и в большую стороны. ¬о-вторых, вследствие неравномерности движени€ воды, наполнение в трубопроводе в отдельных местах может быть больше расчетного. ¬ цел€х исключени€ подтоплени€ трубопроводов при расчетных услови€х наполнение в трубопроводах бытовой водоотвод€щей сети рекомендуетс€ принимать не более 0,8. –екомендуемые максимальные наполнени€ приведены в табл. 2.2.
¬ трубопроводах дождевых сетей (водостоках) полных раздельных систем водоотведени€, а также в общесплавных трубопроводах и общесплавных коллекторах полураздельных систем водоотведени€ при расчетных услови€х наполнение рекомендуетс€ принимать рапным 1, т. е, полным. Ёта объ€сн€етс€ тем, что расчетные услови€ в этих трубопроводах наблюдаютс€ весьма редко 1 раз в 0,25-10 лет. “аким образом, значительную часть времени эти трубопроводы также будут работать при частичном наполнении.
—одержащиес€ в сточных водах нерастворенные примеси способны выпадать в осадок, уменьшать сечение трубопроводов и вызывать их полное засорение. Ќаиболее сложно транспортируютс€ потоком воды минеральные примеси, обладающие большой плотностью. “ранспортирование нерастворенных примесей потоком €вл€етс€ следствием его турбулентности. ѕри определенных малых скорост€х взвешенные вещества осаждаютс€ на дно и образуют плотный слой осадка. ѕри достижении определенной скорости осадок приходит в движение, образу€ слой осадка, имеющий форму непрерывных гр€д, которые движутс€ в направлении потока, но с меньшей скоростью (рис. 2.4). —корость, соответствующа€ началу движени€ осадка, называетс€ размывающей. ѕри дальнейшем увеличении скорости и достижении определенного значени€ весь осадок взвешиваетс€ турбулентным потоком, а трубопровод самоочищаетс€. —корость, соответствующа€ этому моменту, называетс€ самоочищающей. »звестно также пон€тие критической скорости. Ёта скорость Ц соответствующа€ началу осаждени€ примесей (при уменьшении скорости) или полного самоочищени€ (при увеличении скорости). –асход сточных вод в водоотвод€щих сет€х измен€етс€ в широких пределах от определенного минимального до известного максимального, который принимаетс€ за расчетный. ќбеспечить возможность транспортировани€ всех примесей потоком при любом расходе, в том числе и минимальном, не представл€етс€ возможным, так как в этом случае потребовалось бы прокладывать трубопроводы с большими уклонами, а это привело бы к их значительным заглублени€м. ¬ насто€щее врем€ расчет трубопроводов производитс€ на условии поддержани€ труб в чистом состо€нии при максимальном расчетном расходе. “аким образом, при минимальных расходах в трубопроводах допускаютс€ отложени€, но при достижении расчетного расхода трубопроводы должны самоочищатьс€. ѕоэтому при расчете широко используетс€ пон€тие самоочищающа€ скорость. Ёто минимальна€ скорость, котора€ должна обеспечиватьс€ в водоотвод€щих сет€х при расчетном расходе.
|
|
|

–ис. 2.4. —хема непрерывного передвижении отложений в водоотвод€щей сети
ѕрофессоры Ќ. ‘. ‘едоров и ј. ћ. урганов минимальную скорость, которую необходимо соблюдать в трубопроводах из условий самоочищени€, называют незаил€ющей. ƒл€ ее определени€ проф. ». ‘. ‘едоров предложил формулу:
 (2.9)
(2.9)
где ј = 1,42 и n = 4,5+0,5R с учетом корректировки ћ.». јлексеева.
¬. ». алицуном дл€ определени€ самоочищающей скорости получена формула:
 (2.10)
(2.10)
— учетом формулы (2.3)
 (2.11)
(2.11)
где u0 Ц гидравлическа€ крупность Ц скорость осаждени€ частиц песка в поко€щейс€ жидкости.
‘ормула (2.11) учитывает крупность песка, который может содержатьс€ в сточной воде. »зменение крупности песка может быть обусловлено видом сточных вод (бытовые, дождевые, производственные), совершенством покрытий проездов, особенност€ми их содержани€ и др.
—амоочищающа€ скорость зависит и от коэффициента шероховатости n, так как важным источником турбулентности потока €вл€етс€ шероховатость русла. ≈сли в трубопроводах имеетс€ осадок в виде гр€д, то коэффициент n =0,025. ≈сли трубопровод чист, то n =0,01,4. ѕо формуле (2.11) самоочищающа€ скорость в первом случае меньше, чем во втором. ѕервый случай определ€ет услови€ самоочищени€, а второй Ц критические услови€ (услови€, исключающие осаждение взвешенных веществ). ‘ормула (2.11) позвол€ет определ€ть как самоочищающую скорость, так и критическую. ќни различны, так как различны шероховатости русел. Ќо услови€ турбулентности в описанных двух случа€х практически одинаковы.
»тогом всех предшествующих исследований €вл€ютс€ значени€ минимальных скоростей, которые представлены в табл. 2.2. Ёти значени€ близки к тем, которые следуют из формул (2.9) и (2.10).
“аблица 2.2

≈сли в формулу Ўези (2.2) подставить минимальную скорость, то можно получить минимальный уклон, при котором трубопровод самоочищаетс€, и табл. 2.2 приведены минимальные уклоны, соответствующие минимальным скорост€м. ƒл€ труб минимальных диаметров минимальные уклоны приведены в табл. 2.3.
“аблица 2.3

ѕримечание. ¬ скобках указаны уклоны, которые допускаетс€ примен€ть при обосновании.
ѕервоначально она была получена на основании обобщени€ эксплуатационных данных. Ёта формула следует также из формулы (2.11) дл€ конкретных значений u0 и n.
—одержащиес€ в сточных водах песок и другие минеральные примеси €вл€ютс€ абразивными материалами, истирающими стенки трубопроводов в результате транспортировани€ жидкости. ѕри этом интенсивность истирани€ пропорциональна скорости потока, движущегос€ в трубе. ѕоэтому на основании многолетнего опыта эксплуатации водоотвод€щих сетей установлены максимально допустимые скорости, равные 4 м/с Ц дл€ неметаллических труб и 8 м/с Ц дл€ металлических.
|
|
|
ƒл€ определени€ минимального уклона широко известна формула
 (2.12)
(2.12)
где d - диаметр трубопровода, мм;  Ц коэффициент, равный:
Ц коэффициент, равный:

–асчет трубопроводов но формулам (2.1) Ц (2.4) или другим чрезвычайно сложен. ћетоды решени€ различных задач по расчету трубопроводов изложены в специальной литературе.
ѕри проектировании водоотвод€щих сетей требуетс€ выполнить расчеты большого числа отдельных участков трубопроводов с различными услови€ми проектировани€. »х расчет производитс€ путем применени€ тех или иных упрощающих приемов, при которых используютс€ разработанные таблицы, графики, номограммы, различные обобщенные параметры и др.
¬ насто€щее врем€ дл€ расчета самотечных трубопроводов использую; различные таблицы, к числу которых относ€тс€ таблицы ј. ј. Ћукиных и ». Ћ. Ћукиных (“аблицы дл€ гидравлического расчета канализационных сетей и дюкером по формуле акад. ѕ. II. ѕавловского. ћ.: —тройиздат, 1987) и Ќ. ‘. ‘едорова и Ћ. ≈. ¬олкова (√идравлический расчет канализационных сетей. -Ћ.: —тройиздат, 1968). ѕервые составлены по формулам (2.1) Ц (2.4), вторые -по формулам (2.6) и (2.7).
“аблица 2.4
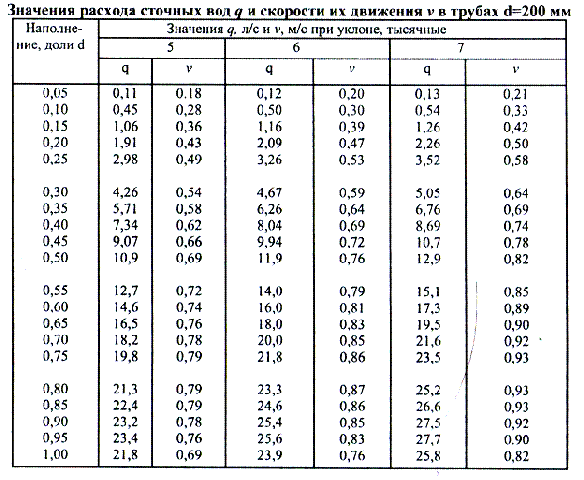
¬ табл. 2.4 приведена кратка€ выдержка из первых таблиц дл€ трубопровода диаметром 200 мм. “аблицы содержат значени€ расхода и скорости при различных наполнени€х от 0,05 до 1,0 дл€ всех возможных в инженерной практике диаметров и уклонов труб.
ѕри проектировании водоотвод€щих сетей предварительно определ€ют расход. ”клон трубопровода принимают с учетом уклона поверхности земли и руководству€сь экономическими соображени€ми (минимальными объемом земл€ных работ и стоимости строительства). –асчет трубопроводов по описанным таблицам сводитс€ к подбору диаметра трубопровода, обеспечивающего пропуск расхода при наполнении, соответствующем самоочищающей скорости.
Ётот расчет весьма прост и удобен. ќднако дл€ него требуютс€ таблицы большого объема, которые издаютс€ отдельными книгами они должны быть Ђпод рукойї у каждою проектировщика, ¬ то же врем€, изданные таблицы не охватывают всех возможных в инженерной практике диаметром и уклонов трубопроводов и параметров их работы
јналогично ведетс€ расчет по графикам и номограммам.
“ехнологический расчет напорных трубопроводов
ƒвижение продукта в напорных трубопроводах происходит полным сечением. –асчет напорных трубопроводов и дюкеров сводитс€ к выбору экономичных диаметров трубопроводов и определению потерь напора.
ƒиаметр трубопровода вычисл€ют из формулы посто€нства расхода  по расчетному расходу q, задава€сь экономичными скорост€ми течени€ v и св€занными соотношени€ми:
по расчетному расходу q, задава€сь экономичными скорост€ми течени€ v и св€занными соотношени€ми:



где qЧ максимальный расчетный расход сточных вод, м3/с;
 - площадь живого сечени€ потока, м2
- площадь живого сечени€ потока, м2
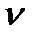 - средн€€ скорость движени€ потока, м/с;
- средн€€ скорость движени€ потока, м/с;
ѕолна€ потер€ напора в напорном трубопроводе H состоит из потери на трение по длине труб  и суммы потерь на преодоление местных сопротивлений
и суммы потерь на преодоление местных сопротивлений  , т. е.
, т. е.

ѕотери напора на трение по длине составл€ют:

√де L Ч длина трубопровода, м; I Ч единична€ потер€ напора или гидравлический уклон;  - коэффициент сопротивлени€ трению.
- коэффициент сопротивлени€ трению.
ѕри движении сточных вод в услови€х шероховатой зоны турбулент≠ного режима потери напора по длине рекомендуетс€ определ€ть по формуле:

ќбычно дл€ подсчета потерь напора по длине пользуютс€ теми же формулами, таблицами и номограммами, что и дл€ расчета сети с учетом полного наполнени€ труб.
ƒл€ приближенных расчетов местные сопротивлени€  длинных трубопроводов принимают равными 10Ч15% потерь на трение hтр. “огда полные потери напора по формуле
длинных трубопроводов принимают равными 10Ч15% потерь на трение hтр. “огда полные потери напора по формуле  принимают:
принимают:
|
|
|
 или
или 
ѕри расчете дюкеров или коротких трубопроводов, в которых потери на местные сопротивлени€ значительны и соизмеримы с потер€ми по длине, необходимо детально учитывать все местные сопротивлени€ по формуле:

где  Ч коэффициент местного сопротивлени€;
Ч коэффициент местного сопротивлени€;
 Ч средн€€ скорость потока, м/с;
Ч средн€€ скорость потока, м/с;
g Ч ускорение свободного падени€, м/с2.
а значени€ коэффициентов местных сопротивлений 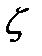 выбирать по табл.
выбирать по табл.
“аблица
«начени€ коэффициента местного сопротивлени€
| ћестные сопротивлени€ | 
|
| ѕри плавном входе в канал | 0,1 |
| “о же, в трубу при острых кромках | 0,5 |
| ѕри выходе из трубы под уровень воды | |
| ¬ задвижке: открытой полностью открытой на ¾ открытой на ½ | 0,5 0,26 2,06 |
| ¬ обратном клапане | |
| ¬ отводе с углом: 30о 45о 75о | 0,07 0,18 0,63 |
| ¬ колене | 0,98 |
ѕолные потери напора в дюкере складываютс€ из суммы потерь на входе в трубу (решетка, уменьшение сечени€ и др.), сопротивлении по длине, на поворотах и на выходе из дюкера.






