Виконання розрахунково-графічного завдання полягає у побудові економетричної функції прибутковості (рентабельності) у формі рівняння регресії цієї функції на змінення двох внутрішньогосподарських факторів виробництва на статистичних даних якісно однорідних підприємств. Виконання розрахунково-графічного завдання складається із 24 кроків, які виконуються на 9 практичних завданнях.
Перелік, позначення, зміст операційних характеристик та одиниці виміру змінних такі:
| ендогенні (залежні) змінні: | ||
доходність витрат (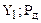 ) )
| – | відношення виручки підприємства від реалізації продукції (робіт, послуг) до їх собівартості, тобто витрат на виробництво, коефіцієнт; |
рівень витрат ( ) )
| _ | відношення собівартості виробленої підприємством продукції (робіт, послуг) до виручки від їх реалізації, коп./грн. або %; |
прибутковість (рентабельність) реалізації (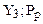 ) )
| – | відношення прибутку підприємства від реалізації продукції (робіт, послуг) до виручки від їх реалізації, коп./грн. або %; |
прибутковість (рентабельність) витрат ( ) )
| – | відношення прибутку підприємства від реалізації продукції (робіт, послуг) до витрат на виробництво, коп./грн. або %; |
| екзогенні (незалежні) змінні | ||
фондоозброєність праці ( ) )
| – | відношення балансової первісної вартості основних виробничих засобів до чисельності працівників підприємства, тис.грн./чол.; |
структура основних виробничих засобів ( ) )
| – | питома вага активних основних виробничих засобів (машин і обладнання) у загальній балансовій первісній вартості основних виробничих засобів, %; |
коефіцієнт придатності ( ) )
| – | відношення залишкової вартості основних виробничих засобів до їх первісної вартості, %; |
енергоозброєність праці ( ) )
| – | відношення сумарної потужності двигунів машин, обладнання тощо до чисельності працівників підприємства, кВТ/чол.; |
спеціалізація підприємства ( ) )
| – | питома вага обсягу реалізації одного (головного) виду продукції (робіт, послуг) в загальному обсязі реалізації, %; |
кооперування виробництва ( ) )
| – | питома вага вартості покупних комплектуючих деталей і вузлів у загальних матеріальних витратах на виробництво продукції (робіт, послуг), %; |
кількість видів продукції (робіт, послуг) ( ) )
| – | кількість найменувань продукції (робіт, послуг), що виробляються підприємством, одиниць; |
питома вага зарплати ( ) )
| – | питома вага витрат на оплату праці в загальній собівартості продукції (робіт, послуг), %; |
бригадна організація праці (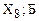 ) )
| – | питома вага робітників, залучених до бригадної форми організації та оплати праці, у загальній чисельності робітників підприємства, %; |
плинність кадрів ( ) )
| – | відношення чисельності звільнених за рік працівників за власним бажанням та за порушення трудової дисципліни до середньорічної чисельності працівників підприємства, %. |
Статистичні дані 15 підприємств про числові значення чотирьох ендогенних (залежних) та десяти екзогенних (незалежних) змінних наведені у табл. 15.1.
Таблиця 15.1 – Статистичні дані 15 підприємств
| j | Змінні | j | |||||||||||||
| ендогенні (залежні) | екзогенні (незалежні) | ||||||||||||||
| Y1 | Y2 | Y3 | Y4 | X0 | X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | X9 | ||
| РД | УЗ | РР | Р | Ф | А | Г | Э | С | К | П | З | Б | Т | ||
| 1,067 | 93,7 | 6,3 | 6,7 | 1,5 | 4,5 | ||||||||||
| 1,073 | 93,2 | 6,8 | 7,3 | 1,7 | 4,8 | ||||||||||
| 1,115 | 89,7 | 10,3 | 11,5 | 6,4 | 16,3 | ||||||||||
| 1,109 | 90,2 | 9,8 | 10,9 | 4,7 | 19,4 | ||||||||||
| 1,054 | 94,9 | 5,1 | 5,4 | 1,6 | 3,5 | ||||||||||
| 1,097 | 91,2 | 8,8 | 9,7 | 4,2 | 11,4 | ||||||||||
| 1,101 | 90,8 | 9,2 | 10,1 | 7,6 | 14,1 | ||||||||||
| 1,114 | 89,8 | 10,2 | 11,4 | 6,9 | 14,9 | ||||||||||
| 1,079 | 92,7 | 7,3 | 7.9 | 2,4 | 6,7 | ||||||||||
| 1,089 | 91,8 | 8,2 | 8,9 | 2,9 | 11,5 | ||||||||||
| 1,095 | 91,3 | 8,7 | 9,5 | 3,8 | 11,9 | ||||||||||
| 1,127 | 88,7 | 11,3 | 12,7 | 7,3 | 21,5 | ||||||||||
| 1,189 | 84,1 | 15,9 | 18,9 | 9,1 | 27,6 | ||||||||||
| 1,098 | 91,1 | 8,9 | 9,8 | 5,6 | 12,1 | ||||||||||
| 1,104 | 90,6 | 9,4 | 10,4 | 7,1 | 13,8 |
Вибір завдання:
Для виконання розрахунково-графічного завдання варіант ендогенної (залежної) змінної 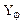 (
( =1,2,3,4) визначається викладачем єдиним для всієї групи. Варіанти двох екзогенних (незалежних) змінних визначаються за останніми двома цифрами номера залікової книжки. Наприклад:
=1,2,3,4) визначається викладачем єдиним для всієї групи. Варіанти двох екзогенних (незалежних) змінних визначаються за останніми двома цифрами номера залікової книжки. Наприклад:
| № залікової книжки | Склад екзогенних (незалежних) змінних - факторів |
| … 01 |  ; ; 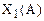
|
| … 27 |  ; ; 
|
| … 30 |  ; ; 
|
Повний перелік варіантів складу факторів наведений вище. Якщо останні дві цифри номера залікової книжки однакові (наприклад, 44, 00 тощо), варіант береться довільно за умови зміни однієї цифри на найближчу (наприклад, 44®43 або 45, або 34, або 54).
Виконання розрахунково-графічного завдання:
Крок 1. Постановка задачі включає: а) вибір змінних та їх операційних характеристик (у прикладі – Р, Ф, К) для складання рівняння регресії щодо варіанта завдання; б) теоретичне обґрунтування наявності та математичної форми кореляційної залежності прибутковості (або рівняння витрат) від обох факторів; в) складання розроблюваного рівня регресії у загальному вигляді. Початкове розуміння сутності розроблюваного рівняння регресії дуже важливе для кількісних і якісних оцінок багатьох попередніх і заключних результатів моделювання.
Крок 2. Матриця статистики складається щодо варіанта завдання за даними 15 підприємств. Наприклад, для варіанта на практичні заняття вона має вигляд (табл. 15.2).
Таблиця 15.2 – Матриця статистики
| № підприємства | Р, коп./грн. | Ф, тис. грн./чол. | К, % |
| … | |||
Матриця статистики характеризується:
· мірністю, тобто кількістю змінних (m+1);
· об'ємом вибірки, тобто кількістю об'єктів спостереження (n);
· об'ємом матриці (m+1)n;
· співвідношенням розмірів матриці n / (m+1), яке для отримання незміщених і дійсних оцінок кореляції і регресії повинно бути не менше восьми. Ця умова порушується, що виправдовується навчальним характером роботи, де процес моделювання набагато вагоміший за кінцевий результат. Скорочення матриці дає виграш у трудомісткості процесу без жодних витрат щодо його змісту та методики виконання.
Крок 3. Показники варіації змінних розраховуються за формулами (наприклад, для змінної Р):
· середня арифметична
 (15.1)
(15.1)
· абсолютний розмах варіації
 (15.2)
(15.2)
· відносний розмах варіації
 (15.3)
(15.3)
· дисперсія (середній квадрат відхилення)
 (15.4)
(15.4)
· середнє квадратичне відхилення
 (15.5)
(15.5)
· коефіцієнт варіації
 . (15.6)
. (15.6)
Розрахунок показників варіації змінних рекомендується внести до табл. 15.3
Таблиця 15.3 – Розрахунок показників варіації змінних (для варіанту Р=f(Ф, К))
| Р | Ф | К | Р2 | Ф2 | К2 | |
| … | ||||||
| Сума | SР | SФ | SК | SР2 | SФ2 | SК2 |
| Середнє | 
| 
| 
| 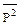
| 
| 
|
| Абсолютний розмах варіації | RP | RФ | RК | |||
| Відносний розмах варіації | іР | іФ | іК | |||
| Квадрат середнього | 
| 
| 
| |||
| Дисперсія | DР | DФ | DК | |||
| Середнє квадратичне відхилення | sР | sФ | sК | |||
| Коефіцієнт варіації | nР | nФ | nК |
Крок 4. Поля кореляції (графічні зображення залежності) будуються за матрицею статистики (табл. 15.2) на міліметровому папері формату А4. Масштаб зображення за осями координат вибирається таким, щоб поле кореляції виглядало "стоячим", якщо  (рис. 15.1,а), "лежачим", якщо
(рис. 15.1,а), "лежачим", якщо  (рис. 15.1,б) або квадратним, якщо
(рис. 15.1,б) або квадратним, якщо  (рис.15.1, в).
(рис.15.1, в).
| а) | б) | в) |

| 
| 
|
Рис. 15.1 – Типи полів кореляції
Розмітка координаційної сітки диктується мінімальними і максимальними значеннями змінних, тому площина полів повинна використовуватися повністю. На "міліметрівці" повинно лишатися вільне місце з усіх боків, бо до полів кореляції знадобиться звертатися багаторазово для виконання на них розрахункових операцій та графічних побудов (кроки 5, 8, 9, 19, 23).
Аналіз полів кореляції проводиться з метою визначення за графічними критеріями:
· наявності кореляційних залежностей;
· напряму та математичної форми залежностей;
· кількісної однорідності об'єктів спостереження, зокрема, наявності аномальних об'єктів.
Крок 5. Аномальні об'єкти спостережень, тобто об'єкти, що "випадають" із вибіркової сукупності на полях кореляції, визначаються так:
1) на поле кореляції накладається прямокутний шаблон двомірного розсіювання з центром у точці  та напівсторонами
та напівсторонами  і
і  (рис. 15.7). Коефіцієнт довіри
(рис. 15.7). Коефіцієнт довіри  береться за таблицею t-розподілу Ст’юденту залежно від кількості об'єктів спостереження і бажаної імовірності. За умови, що
береться за таблицею t-розподілу Ст’юденту залежно від кількості об'єктів спостереження і бажаної імовірності. За умови, що  =15 і
=15 і  =0,95,
=0,95,  =1,76.
=1,76.
|
|
|
|
|
|
|
|
|

|
Рис. 15.2 – Шаблони для виявлення аномальних об'єктів спостереження
Об'єкти спостереження, які знаходяться на полі кореляції за межами прямокутного шаблону двомірного розсіювання, вважаються аномальними 1-го роду;
2) на поле кореляції наноситься "коридор регресії". Його вісь – це діагональ прямокутного шаблону розсіювання, навколо якої розташовані точки поля кореляції (додатна або від'ємна), а напівширина – це величина, що визначається залежно від бажаної імовірності та щільності полів кореляції за формулою
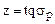 , (15.8)
, (15.8)
де  – коефіцієнт довіри за таблицею нормального розподілу (якщо Р=0,95, то
– коефіцієнт довіри за таблицею нормального розподілу (якщо Р=0,95, то  =1,96);
=1,96); 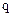 – коефіцієнт щільності поля кореляції, який приймається за шкалою:
– коефіцієнт щільності поля кореляції, який приймається за шкалою:
дуже щільне ……………. 0,53
щільне ……………...…… 0,72
середньої щільності ……. 0,80
"пухке" ……………..…… 0,87
дуже "пухке" ………….… 0,92
Об'єкти спостереження, що знаходяться за межами "коридору регресії", вважаються аномальними 2-го роду (див. рис. 15.2).
Крок 6. Для прийняття рішень щодо аномальних об'єктів спостереження складається зведення аномальних об'єктів (табл. 15.4).
Таблиця 15.4 – Зведення аномальних об'єктів спостереження
| № аномальних об'єктів | 1-го роду | 2-го роду | Рішення | ||
| Ф | К | Ф | К | ||
| – | + | – | – | залишається в матриці | |
| + | + | – | + | вилучається з матриці |
У табл. 15.4 вносяться всі аномальні об'єкти, виявлені на полях кореляції РФ і РК за критеріями випадань за межі прямокутника двомірного розсіювання (1-й рід) та "коридору регресії" (2-й рід). Рішення приймається за більшості знаків "+" (випадання) або "–" (не випадання). Якщо кількість знаків "+" і "–" однакова, рішення приймається з урахуванням більшої значущості випадань 2-го роду.
Крок 7. Вилучення з матриці аномальних об'єктів викликає необхідність коригування показників варіації змінних (див. крок 3). Для цього з табл. 15.4 вилучаються відповідні рядки і перераховуються всі показники, починаючи з рядка "сума".
Крок 8. Аналітична перевірка наявності кореляційних залежностей здійснюється на доповнення теоретичній (див. крок 1) та графічній (див. крок 4) шляхом визначення коефіцієнтів Фехнера або асоціації. Для розрахунку цих коефіцієнтів на поля кореляції наносяться лінії  і
і  , завдяки чому об'єкти спостереження діляться на чотири підгрупи:
, завдяки чому об'єкти спостереження діляться на чотири підгрупи:
а – кількість об'єктів у лівій верхній чверті поля;
b – те саме у правій верхній;
c – те саме у лівій нижній;
d – те саме у правій нижній.
Очевидно, що a+b+c+d=n. Ці підрахунки виконуються на полях кореляції і на них фіксуються.
Коефіцієнт Фехнера визначається за формулою
 , (15.9)
, (15.9)
а коефіцієнт асоціації
 . (15.10)
. (15.10)
Ці коефіцієнти приймають значення від –1 до +1. Якщо вони рівні або близькі до нуля, то кореляційна залежність практично відсутня. Чим ближче значення коефіцієнтів до одиниці, тим наявна залежність сильніша. Знаки  і
і  показують лише напрямок залежності – додатний, або від'ємний – і до оцінки її сили не мають відношення.
показують лише напрямок залежності – додатний, або від'ємний – і до оцінки її сили не мають відношення.
Крок 9. Перевірка суттєвості (невипадковості) кореляційних залежностей здійснюється за дисперсійним F-критерієм Фішера у наступному порядку (для кожного фактора):
1) на полях кореляції проводиться групування об'єктів по  в інтервалах, що визначаються за формулою Стерджеса (з округленням)
в інтервалах, що визначаються за формулою Стерджеса (з округленням)
 , (15.11)
, (15.11)
підраховується кількість об'єктів у кожній групі (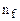 ) і визначаються групові середні показники рентабельності
) і визначаються групові середні показники рентабельності  . Кількість груп дорівнює К, очевидно, що
. Кількість груп дорівнює К, очевидно, що  ;
;
2) визначається міжгрупова. систематична дисперсія рентабельності
 , (15.12)
, (15.12)
а також внутрішньогрупова залишкова дисперсія рентабельності
 ; (15.13)
; (15.13)
3) визначається розрахункове значення дисперсійного відношення
 (15.14)
(15.14)
і в залежності від кількості ступенів вільності (к-1) та (n-к) за таблицею F-розподілу Снедекера знаходиться критичне значення  ;
;
4) розрахункове значення відношення зіставляється з критичним. Якщо  , то з імовірністю 0,95 кореляційна залежність Р від
, то з імовірністю 0,95 кореляційна залежність Р від  є суттєвою, тобто невипадковою і навпаки.
є суттєвою, тобто невипадковою і навпаки.
Наведені вище розрахунки з дисперсійного аналізу оформляються в таблицях (див. табл. 15.5).
Таблиця 15.5 – Розрахунок систематичної і залишкової дисперсії рентабельності*
| Інтервали по Ф |

|

| 
|

| Систематична | Залишкова | |||

| 
| 
| 
| 
| |||||
| 0 – 1,5 | 6,7 | 6,7 | 6,700 | -2,743 | 7,524 | 7,524 | |||
| 1,5 – 3 | 5,4; 7,3; 7,9; 8,9 | 29,5 | 7,375 | -2,068 | 4,277 | 17,108 | 3,901; 0,006; 0,276; 2,326 | 6,509 |
Продовження табл. 15.5
…

| |||||||||
| Всього |  =132,2 =132,2
|  =132,2 =132,2
|  =9,443 =9,443
|  =
=43,684 =
=43,684
|  =
=9,795 =
=9,795
| ||||
| Кількість ступенів вільності | 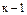 =6-1 =6-1
|  =14-6 =14-6
| |||||||
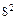
| 8,737 | 1,224 |
Фрагмент таблиці F-розподілу Снедекора для визначення  з імовірністю 0,95 наводиться нижче:
з імовірністю 0,95 наводиться нижче:
| n-к | к-1 | |||
| 3,84 | 3,69 | 3,58 | 3,50 | |
| 3,63 | 3,48 | 3,37 | 3,29 | |
| 3,48 | 3,33 | 3,22 | 3,14 | |
| 3,36 | 3,20 | 3,09 | 3,01 | |
| 3,26 | 3,11 | 3,00 | 2,92 |
Фактор, вплив якого за F-критерієм визначається несуттєвим, випадковим, вилучається з матриці статистики і з подальшого процесу моделювання.
Крок 10. Для розрахунку коефіцієнтів кореляції необхідно попередньо виконати розрахунок середніх добутків змінних (табл. 15.6),
Таблиця 15.6 – Розрахунок середніх добутків змінних
| j | РФ | РК | ФК |
| … | |||
| Сума | SРФ | SРК | SФК |
| Середній добуток | 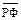
| 
| 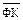
|
після чого виконати розрахунок коефіцієнтів кореляції за формулами
 . (15.15)
. (15.15)
Коефіцієнти кореляції показують напрямок і силу впливу факторів на рентабельність ("+" – додатний, "–" – від'ємний). Слід мати на увазі, що  .
.
Крок 11. Наявність і сила мультиколінеарності факторів, тобто взаємозв'язку між ними, оцінюється за повною матрицею коефіцієнтів кореляції


за наступною шкалою оцінок (за модулями коефіцієнтів кореляції для загального випадку  :
:
 – відсутня,
– відсутня,
 – слабка,
– слабка,
 – помірна,
– помірна,
 – сильна,
– сильна,
 – абсолютна, з двох факторів один є зайвим.
– абсолютна, з двох факторів один є зайвим.
Крок 12. Розрахунок коефіцієнтів парціальної кореляції особливо важливий при сильній мультиколінеарності факторів. Ці коефіцієнти визначають напрямок і силу впливу факторів за умови очищення цих оцінок від викривлення через мультиколінеарність. Вони розраховуються за формулою
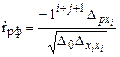 , (15.16)
, (15.16)
де  – визначник (детермінант) повної матриці коефіцієнтів кореляції з вилученням з неї стовпця
– визначник (детермінант) повної матриці коефіцієнтів кореляції з вилученням з неї стовпця  і рядка
і рядка  ;
;  – те саме з вилученням з неї стовпця і рядка Р;
– те саме з вилученням з неї стовпця і рядка Р;  – те саме з вилученням з неї стовпця і рядка
– те саме з вилученням з неї стовпця і рядка  ;
;  – номера вилучених стовпця і рядка матриці при розрахунку визначника
– номера вилучених стовпця і рядка матриці при розрахунку визначника  . Наприклад (див. крок 11):
. Наприклад (див. крок 11):
 .
.
Крок 13.  -коефіцієнти, які також визначають напрямок і силу впливу факторів на рентабельність з урахуванням мультиколінеарності, розраховуються за формулою
-коефіцієнти, які також визначають напрямок і силу впливу факторів на рентабельність з урахуванням мультиколінеарності, розраховуються за формулою
 , (15.17)
, (15.17)
де  – визначник (детермінант) матриці взаємної кореляції (мультиколінеарності) із заміною в ній і-го стовпця стовпцем коефіцієнтів
– визначник (детермінант) матриці взаємної кореляції (мультиколінеарності) із заміною в ній і-го стовпця стовпцем коефіцієнтів
кореляції  . Наприклад (див. кроки 11 і 12):
. Наприклад (див. кроки 11 і 12):
 .
.
Крок 14. Розрахунок коефіцієнта множинної кореляції необхідний для визначення сили впливу на рентабельність обох факторів разом, він розраховується за формулою Боярського
 , (15.18)
, (15.18)
де  – порядок повної матриці коефіцієнтів кореляції;
– порядок повної матриці коефіцієнтів кореляції;  – визначник повної матриці коефіцієнтів кореляції із заміною нижнього правого елемента нулем.
– визначник повної матриці коефіцієнтів кореляції із заміною нижнього правого елемента нулем.
У нашому прикладі формула Боярського має вигляд
 .
.
З метою контролю правильності розрахунків рекомендується цей коефіцієнт визначати також за такою формулою:
 . (15.19)
. (15.19)
Значення коефіцієнта повинні співпадати, розбіжність можлива лише в кілька тисячних або десятитисячних за рахунок округлення в розрахунках.
Крок 15. Оцінка сили впливу факторів на рентабельність за допомогою U-критерія Фішера з імовірністю 0,95:
 1,96,
1,96,
де  – розрахункове значення U, що визначається за формулою
– розрахункове значення U, що визначається за формулою
 . (15.20)
. (15.20)
Якщо  1,96,сила впливу
1,96,сила впливу  на
на  з імовірністю 0,95 визначається достатньою для подальшої участі
з імовірністю 0,95 визначається достатньою для подальшої участі  у процесі моделювання.
у процесі моделювання.
Крок 16. Оцінка незалежності (автономності) впливу факторів на рентабельність визначається за допомогою  -критерія
-критерія
 ,
,
де  – рівень автономності, що розраховується за формулою
– рівень автономності, що розраховується за формулою
 . (15.21)
. (15.21)
Якщо  >0, фактор
>0, фактор  має певну автономність впливу на рентабельність;
має певну автономність впливу на рентабельність;  =0 – ніякої автономності він не має і його вплив на рентабельність через мультиколінеарність проявляється завдяки іншим факторам;
=0 – ніякої автономності він не має і його вплив на рентабельність через мультиколінеарність проявляється завдяки іншим факторам;  <0 – у такому випадку і-й фактор вилучається з подальшого процесу розробки рівняння регресії.
<0 – у такому випадку і-й фактор вилучається з подальшого процесу розробки рівняння регресії.
Крок 17. Значущість впливу факторів на рентабельність оцінюється на основі коефіцієнтів множинної кореляції за  -критерієм
-критерієм
 1,96,
1,96,
де
 (
( =1,2;
=1,2;  ) (15.22)
) (15.22)
У нашому прикладі формула (3.21) для визначення 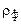 і
і  набуває такого вигляду:
набуває такого вигляду:
 ;
;
 .
.
Якщо  1,96, то з імовірністю 0,95 можна стверджувати, що вплив фактора
1,96, то з імовірністю 0,95 можна стверджувати, що вплив фактора  достатньо значущий, вагомий для включення його у рівняння регресії.
достатньо значущий, вагомий для включення його у рівняння регресії.
Крок 18. Для прийняття рішення щодо включення факторів у рівняння регресії складається зведення результатів, одержаних на кроках 15, 16, 17 (табл. 15.7).
Таблиця 15.7 – Зведення оцінок сили, автономності та значущості впливу факторів
| Фактори | Ui Ui³1,96 | gi 0<gi<1 | ri
 ri³1,96 ri³1,96
| Рішення |
| Ф | ||||
| К |
Поради щодо прийняття рішень такі:
· якщо  ,
,  вилучається з матриці (див. крок 16);
вилучається з матриці (див. крок 16);
· значення  та
та  дуже залежать від об'єму вибірки (див. формули (15.20) і (15.22)), тому рішення приймається з огляду на порушення вимоги
дуже залежать від об'єму вибірки (див. формули (15.20) і (15.22)), тому рішення приймається з огляду на порушення вимоги  . Отже, якщо критерії
. Отже, якщо критерії  та
та  виконуються не в повній мірі, обидва фактори треба включати до рівняння регресії.
виконуються не в повній мірі, обидва фактори треба включати до рівняння регресії.
Крок 19. Дляобґрунтування математичної форми рівняння регресії необхідно скористатися раніше сформульованими щодо цього висновками з теоретичного обґрунтування (див. крок 1), а також з візуального аналізу полів кореляції (див. крок 4). Ці джерела вибору математичної форми рівняння регресії (пряма, гіпербола, парабола тощо) достатньо надійні і ними можна обмежитися.
Для аналітичного підтвердження правильності вибору форми регресії можна користуватися способом перших різниць з використанням результатів кроку 9. Нарешті, не буде великої помилки, якщо форма регресії буде прийнята лінійною і модель рівняння регресії матиме такий вигляд (для нашого прикладу):
 , (15.23)
, (15.23)
де  – коефіцієнти регресії. Коефіцієнт
– коефіцієнти регресії. Коефіцієнт 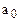 показує частину
показує частину  , що не залежить від факторів
, що не залежить від факторів  і
і 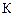 ;
;  визначає, на скільки копійок змінюється
визначає, на скільки копійок змінюється  за рахунок зміни Ф на одну тисячу гривень;
за рахунок зміни Ф на одну тисячу гривень;  визначає зміну
визначає зміну  в копійках при зміні
в копійках при зміні 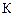 на один відсоток.
на один відсоток.
Крок 20. Для розрахунку коефіцієнтів регре сії  та
та  методом найменших квадратів слід скласти систему нормальних рівнянь і вирішити її. У нашому прикладі в разі вибору лінійної форми регресії ця система така:
методом найменших квадратів слід скласти систему нормальних рівнянь і вирішити її. У нашому прикладі в разі вибору лінійної форми регресії ця система така:
 . (15.24)
. (15.24)
Числові значення параметрів цієї системи беруть за табл. 1.3 (крок 3 з урахуванням коригування на кроці 7), 1.6 (крок 10).
Для контролю правильності розрахунків коефіцієнтів регресії рекомендується варіант розрахунку їх через  -коефіцієнти, а саме:
-коефіцієнти, а саме:
 ,
,  . (15.25)
. (15.25)
Ця перевірка можлива за умови, що обидва фактори включені до рівняння регресії. Отже, модель рівняння регресії (1.22) прийме конкретний вигляд.
Крок 21. Розрахунок оцінок рентабельності за рівнянням регресії необхідний, по-перше, для контролю правильності розрахунку коефіцієнтів регресії і, по-друге, для визначення помилок апроксимації. Розрахунки доцільно ввести до табл. 15.8.
Таблиця 15.8 – Розрахунок оцінок рентабельності
| № підприємства | Рj | Розрахунок оцінок | Помилка апроксимації

| Те саме, % | |||
| а0 | а1Ф | а2К | 
| ||||
| Всього | SРj | X | X | X | S
| X |
Необхідною (хоча і не достатньою) умовою правильності розрахунку коефіцієнтів регресії є
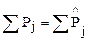 .
.
Крок 22. Розрахунок кореляційного відношення проводиться за формулою
 , (15.26)
, (15.26)
де  – дисперсія оцінок рентабельності, визначених у табл. 15.8, яка
– дисперсія оцінок рентабельності, визначених у табл. 15.8, яка
розраховується так само, як і дисперсія фактичних значень, за формулою (15.26), тобто в даному разі
 .
.
Слід пам'ятати, що, оскільки  , то
, то  . Для визначення середнього квадрату оцінок рентабельності слід скласти табл. 15.9.
. Для визначення середнього квадрату оцінок рентабельності слід скласти табл. 15.9.
Таблиця 15.9 – Розрахунок середнього квадрату оцінок рентабельності
| № підприємства | 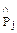
| 
|
| Сума | 
| 
|
| Середнє | 
| 
|
Величина дисперсії  береться за таблицею кроку 7.
береться за таблицею кроку 7.
Для контролю правильності визначення  слід керуватися наступним:
слід керуватися наступним:
1) якщо обидва фактори залишилися у рівнянні регресії, то (див. крок 14)  ;
;
2) якщо до рівняння регресії введено тільки один (і-й) фактор, то  .
.
Крок 23. Розрахунок помилки апроксимації включає:
· визначення середньої помилки апроксимації за формулою
 ; (15.27)
; (15.27)
· визначення граничної помилки апроксимації з певною імовірністю її неперевищення. Якщо прийнятна імовірність 0,95, то гранична помилка така:
 . (15.28)
. (15.28)
Гранична помилка апроксимації є довірчою границею визначення  за рівнянням регресії (Р =0,95)
за рівнянням регресії (Р =0,95)
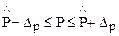 .
.
Бажано перевірити виконання цієї умови за даними табл. 15.9.
Крок 24. Економічна інтерпретація рівняння регресії повинна включати:
1) операційні характеристики змінних (у нашому прикладі Р, Ф і К – див. крок 1);
2) розкриття змісту та одиниці виміру коефіцієнтів регресії 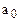 ,
,  і
і  - див. крок 19);
- див. крок 19);
3) те саме довірчої границі помилки апроксимації;
4) оцінку якості отриманого рівняння регресії, у нашому прикладі
 (Р =0,95).
(Р =0,95).
У висновках бажано вказати, для яких цілей можна використовувати отримане рівняння регресії рентабельності.
* Для наочності розрахунків табл.1.5 частково заповнена.






