ПРИБЛИЖЕННОЕ ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
ЦЕЛЬ РАБОТЫ
Ознакомится с численными методами вычисления определенных интегралов, научится решать задачи с использованием формулы Симпсона, трапеций, правых и левых прямоугольников, метод Монте-Карло.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. Изучить теоретическую часть. Выполните задания, соответствующие номеру Вашего варианта, и продемонстрируйте их преподавателю.
2. Оформите отчет по лабораторной работе, который должен содержать:
· титульный лист;
· исходные данные варианта;
· решение задачи;
· результаты решения задачи.
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
Пример 9.1.
Вычислить интеграл 
методом левых и правых прямоугольников, трапеций и Симпсона.
Решение:
В командном окне программы МАТLAB наберем следующую последовательность операторов:
>> f=inline('reallog(x)'); % задание подынтегральной функции
>> a=3;
>> b=5;
>> N=100;
>> i=1:N;
>> dx=(b-a)/(N-1); % шаг интегрирования
>> x=a:dx:b; % вычисление координат узлов сетки
>> y=feval(f,x); % вычисление значений функции в узлах сетки
% вычисление интеграла методом правых прямоугольников
>> m=2:N;
>> y1(m-1)=y(m);
>> Fr=sum(y1)*dx
Fr =
2.7565
% вычисление интеграла методом левых прямоугольников
>> m=1:N-1;
>> y1(m)=y(m);
>> Fl=sum(y1)*dx
Fl =
2.7462
% вычисление интеграла методом трапеций
>> s=0;
>> for i=2:N-1
s=s+y(i);
end;
>> Ft=(0.5*y(1)+s+0.5*y(N))*dx
Ft =
2.7513
% вычисление интеграла методом Симпсона
>> s=0;
>> for i=2:N-1
if i-2*ceil(i/2)==0
k=4;
else
k=2;
end;
s=s+k*y(i);
end;
>> Fs=(y(1)+s+y(N))*dx/3
Fs =
2.7405
Пример 9.2.
Вычислить интеграл методом Монте-Карло.
Решение:
Значение интеграла можно вычислить по формуле:
, (9.1)
где n – число точек, удовлетворяющих условию 
, N – полное количество точек, S – площадь прямоугольника;
или:
, (9.2)
где xi – последовательность случайных чисел с равномерным законом распределения на отрезке [ a, b ].
В командном окне программы МАТLAB введем следующее:
>> f=inline('reallog(x)');
>> a=3; % задание координат вершин прямоугольника
>> b=5;
>> Ymin=0;
>> Ymax=feval(f,b);
>> N=1000; % генерация случайных координат
>> x=a+(b-a)*rand(N,1);
>> y=Ymin+(Ymax-Ymin)*rand(N,1);
>> s=0; % подсчет числа точек, попавших под график функции
>> for i=1:N
if y(i)<=feval(f,x(i))
s=s+1;
end;
end;
>> Fmk=s*(b-a)*(Ymax-Ymin)/N % вычисление значения интеграла
Fmk =
2.7425
% вычисление интеграла в соответствии с (9.2)
>> F=feval(f,x);
>> Fmk=(b-a)*sum(F)/N
Fmk =
2.7463
Вычисление интеграла в системе MATLAB осуществляется с помощью следующих функций:
ü quad(¢fun¢, a, b, tol) – возвращает значение интеграла от функции fun на интервале [a, b] с заданной относительной погрешностью tol (по умолчанию tol=10-3), при вычислении используется адаптивный метод Симпсона;
ü int(y(x), a, b) – возвращает значение интеграла от функции y(x) на интервале [a, b] аналитическими методами (если границы не задавать, то вычисляет неопределенный интеграл).
Пример 9.3.
Пусть необходимо вычислить определенный интеграл
.
Программа решения интеграла с помощью функции quad имеет вид:
>> y='log(x)';
>> quad(y,3,5)
После нажатия клавиши <Enter> получим следующее решение:
ans =
2.7514
Рассмотрим решение интеграла с помощью функции int:
>> syms x; %определение символьных переменных
>> y=log(x); % ввод подынтегрального выражения
>> int(y,3,5)
ans =
5*log(5)-2-3*log(3)
ЗАДАНИЕ
Найти приближенное значение интеграла заданной функции f (x) на отрезке [ a, b ] по формулам прямоугольников, трапеции, Симпсона, Монте-Карло при делении отрезка на 2000 равных частей
Варианты заданий.
| № варианта | f (x) | [ a, b ] | № варианта | f (x) | [ a, b ] |
| [0; 3] | 
| [1,5;2,5] | ||
| [0; 1] | 
| [1; 7] | ||
| [1; 2] | 
| [0; 1] | ||
| [2; 3] | 
| [0; 3] | ||
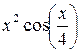
| [2; 3] | 
| [0;  ]
| ||
| [1; 2] | 
| [0; 5] |
Варианты заданий.
| № варианта | f (x) | [ a, b ] | № варианта | f (x) | [ a, b ] |
|
| [0; 3] |
| [1,5;2,5] | ||
|
| [0; 1] |
| [1; 7] | ||
|
| [1; 2] |
| [0; 1] | ||
|
| [2; 3] |
| [0; 3] | ||
|
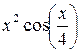
| [2; 3] |
| [0; ]
| ||
|
| [1; 2] |
| [0; 5] |
Методы численного интегрирования
- Аналитическое интегрирование средствами MATLAB.
- Аналитическое дифференцирование средствами MATLAB.
- Теоретическая оценка погрешности численного интегрирования.
- Численное интегрирование
- Численное интегрирование средствами MATLAB
- Правило Рунге оценки погрешности интегрирования
К вычислениям определенных интегралов сводятся многие практические задачи физики, химии, экологии, механики и других естественных наук. На практике взять интеграл аналитически не всегда удается. В этом случае используются методы численного интегрирования. В данной лабораторной работе рассматриваются методы Ньютона - Котеса, в частности методы прямоугольников, трапеций и Симпсона (парабол). Кроме того, в лабораторной работе рассматриваются способы аналитического и численного отыскания интегралов средствами MATLAB.
Вычислительные формулы для всех рассматриваемых методов приведены в приложении, теоретический материал следует изучать по материалам лекций и рекомендованной литературе. Здесь же будут рассмотрены практические аспекты реализации методов численного интегрирования в MATLAB.
Вам следует внимательно изучить и выполнить приведенные здесь примеры, может быть для функций из ваших вариантов задач.
