Циклический– процесс многократного повторения некоторого участка вычислений при изменении хотя бы одной из входящих в него величин.
Математически циклический процесс выражается зависимостью
y i = f(x i),
т.е. предписывает многократное вычисление функции yi в соответствии с изменением аргумента xi. С точки зрения цикла аргумент xi является входной, а функция yi выходной величинами (данными).
Сформулируем основные определения.
Цикл – повторяющийся участок вычисления.
Тело цикла – совокупность действий, осуществляемых в цикле.
Параметр цикла – входная величина, изменяющая своё значение от цикла к циклу.
Закон изменения параметра цикла – зависимость, связывающая текущее и предыдущее значения параметра цикла.
Условие повторения цикла – зависимость, предписывающая повторение цикла либо выход из него.
Все циклические процессы по способу определения количества повторений (N) разделяются на два класса (рис. 5.1).

Рис. 5.1. Классификация циклов по количеству повторений
Арифметический – циклический процесс, число повторений в котором может быть определено заранее, т.е. не зависит от результатов счёта в теле цикла.
Итерационный – циклический процесс, число повторений в котором зависит от результатов вычислений в теле цикла и не может быть определено заранее.
К арифметическим циклам, как правило, относятся вычисления вида yi = f(x i), к итерационным – yi = f(yi - 1).
Независимо от того, к какому классу относится вычислительный процесс, каждый из них содержит обязательные элементы:
· вход в цикл (формирование начального значения параметра цикла);
· вычисления в теле цикла (расчёт текущего значения функции, формирование нового значения параметра цикла и вспомогательные операции);
· выход из цикла (проверка условия, определяющего повторение вычислений либо их прекращение).
По своему содержанию эти элементы зависят от класса и особенностей цикла, в котором используются.
Рассмотрим варианты организации циклических процессов арифметического типа.
Арифметические циклы характеризуются следующей постановкой задачи:
рассчитать текущие значения функции yi = f (xi) при изменении аргумента (параметра цикла) в заданном диапазоне xн 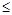 xi
xi 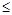 xк (1
xк (1 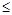 i
i 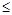 N) по известному закону x i = j (x i - 1), (ij = j (ij – 1)).
N) по известному закону x i = j (x i - 1), (ij = j (ij – 1)).
При этом количество повторений цикла (N) может быть определено (задано) до начала вычислений.
В соответствии с видом задания (изменения) параметра цикла арифметические циклы классифицируются схемой (рис. 5.2):

Рис. 5.2. Классификация арифметических циклов
Табуляция функции – многократное вычисление значений функции при изменяющихся значениях аргумента.
Результаты табуляции представляются в виде табл. 5.1.
Таблица 5.1
| Аргумент | Функция |
| xн | yн |
| ... | ... |
| xi | yi |
| ... | ... |
| xn | yn |
Рассмотрим методику программирования арифметических циклов при различных видах изменения аргумента.
Арифметические циклы с аналитическим заданием аргумента
К классу циклических процессов с аналитическим заданием (изменением) аргумента относятся вычислительные процессы вида
yi = f(xi),
в которых аргумент изменяется по заданному закону.
Аналитический– закон изменения параметра цикла вида
x i = j (x i - 1).
Как правило, в качестве такого закона используют простейшую зависимость:
x i = x i - 1 + Dx.
При этом диапазон изменения параметра xi задаётся начальным (xн) и конечным (xк) значениями. Математическая формулировка условия нахождения xi в диапазоне счёта зависит от конкретных численных значений xн, xк и Dx.
При xн<xк и положительных Dx оно запишется как xн 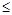 xi
xi 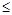 xк.
xк.
При xн>xк и отрицательном Dx получим xн  xi
xi  xк.
xк.
Варианты изменения параметра цикла xi при увеличивающихся значениях искомых yi представлены на рис. 5.3. Стрелки под осями абсцисс определяют направление изменения параметра цикла.
 Y Y
Y Y
xн 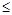 xi
xi 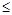 xк xн
xк xн  xi
xi  xк
xк
yк yк
Dx положительно Dx отрицательно
yi yi
yн yн
Dx Dx
xн xi xк X xк xi xн X
Рис. 5.3 Варианты изменения параметра цикла
Сформулированные двойные неравенства позволяют выделить из них конкретные элементы цикла:
· начальное значение параметра xi=xн (левая часть неравенства);
· условие повторения цикла (правая часть неравенств) xi 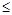 xк при положительном Dx (xi
xк при положительном Dx (xi  xк при отрицательном Dx), невыполнение которого приводит к выходу из цикла.
xк при отрицательном Dx), невыполнение которого приводит к выходу из цикла.
Дополнив полученные элементы входа в цикл и выхода из него конкретной основной зависимостью yi = f (xi) и стандартным законом xi = xi-1 + Dx, получим все необходимые компоненты арифметического цикла с аналитическим изменением параметра.
Принадлежность цикла к классу арифметических подтверждается тем, что количество повторений в нём может быть определено заранее по формуле N = ] (xк - xн ) / Dx [ + 1. Обратные квадратные скобки предписывают от полученного частного учитывать только целую часть.
Рассмотрим программирование задач этого класса на конкретной задаче (5.1) о подоходных налогах.
Постановка задачи
Рассчитать величину подоходного налога на работников предприятия, если известно, что зарплата может изменяться в диапазоне от 2842 до 5500 р. с шагом изменения 300 р., а налог составляет 13 % от зарплаты.






