I. Интегралы вида:
1) 
2) 
где a,b,c,d – действительные числа, р1,…, рk, q1,…qk – целые числа,
n1,…, nk, m1,…mk – натуральные числа.
Для их решения следует применять подстановки:
1) 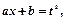 где s – наименьшее общее кратное чисел n1,…, nk
где s – наименьшее общее кратное чисел n1,…, nk
2)  где s – наименьшее общее кратное чисел m1,..., mk
где s – наименьшее общее кратное чисел m1,..., mk
Для решения примеров также необходимо вспомнить:
1) формулы сокращенного умножения;
2) свойства степеней.



 Пример 1.
Пример 1.





 Пример 2.
Пример 2.
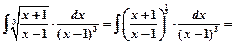


II. Интегралы вида 
где а, b – действительные числа, m, n, p – рациональные числа.
Выражение  называется дифференциальным биномом, его интегрирование возможно только в трех случаях.
называется дифференциальным биномом, его интегрирование возможно только в трех случаях.
1) р – целое число,
тогда используем постановку 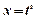 , где s – наименьшее общее кратное знаменателей дробей m и n.
, где s – наименьшее общее кратное знаменателей дробей m и n.
2)  - целое число,
- целое число,
тогда  где k - знаменатель дроби p.
где k - знаменатель дроби p.
3)  - целое число,
- целое число,
тогда  (или
(или  ), где k - знаменатель дроби p.
), где k - знаменатель дроби p.
Во всех остальных случаях интегралы от дифференциального бинома являются «неберущимися».
Пример 1.

 Пример 2.
Пример 2.


Пример 3.

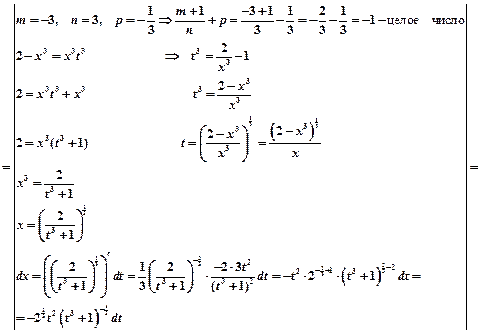


Подстановки Эйлера
Интеграл вида  можно свести к интегралу от рациональной функции с помощью подстановок Эйлера.
можно свести к интегралу от рациональной функции с помощью подстановок Эйлера.
1) Если  , то используем 1 подстановку Эйлера
, то используем 1 подстановку Эйлера 
возведя оби части равенства в квадрат, можно найти  и
и  .
.
2) Если  , то используем 2 подстановку Эйлера
, то используем 2 подстановку Эйлера 
преобразования аналогичны.
3) Если квадратный трехчлен  имеет два действительных корня
имеет два действительных корня  и
и  , то применяем 3 подстановку Эйлера
, то применяем 3 подстановку Эйлера  причем неважно какой корень взять.
причем неважно какой корень взять.
Замечание 1.
При использовании 1 и 2 подстановок Эйлера знак «+» или «-» выбирается, исходя из условия так, чтобы полученная рациональная функция максимально упростилась.
Замечание 2.
Прежде чем применить подстановки Эйлера, нужно внимательно посмотреть на интеграл.
Если он имеет вид  , то рациональнее решить с помощью выделения полного квадрата (см. стр. 15).
, то рациональнее решить с помощью выделения полного квадрата (см. стр. 15).
Если он имеет вид  или
или  , то лучше применить подстановку
, то лучше применить подстановку  (см. стр. 9)
(см. стр. 9)
Замечание 3.
На самом деле достаточно использовать только 1 и 3 подстановки Эйлера.
Пример 1.


Пример 2.


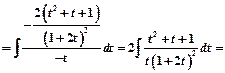
 Пример 3.
Пример 3.




Пример 4.





Пример 5.



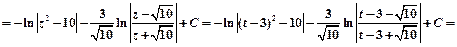

Приложения:
1. Формулы сокращенного умножения.
2. Свойства степеней.
3. Свойства логарифмов.
4. Тригонометрические формулы.
5. Таблица производных.
6. Правила дифференцирования.
7. Таблица дифференциалов.
Формулы сокращенного умножения

Свойства степеней
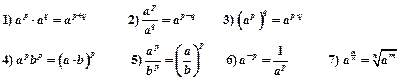
где p, q – рациональные числа, m – целое число, n – натуральное число
Свойства логарифмов

где 
Тригонометрические формулы

Таблица производных

Правила дифференцирования
1)  2)
2) 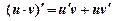
3)  4)
4) 
5)  6)
6) 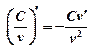
Таблица дифференциалов







