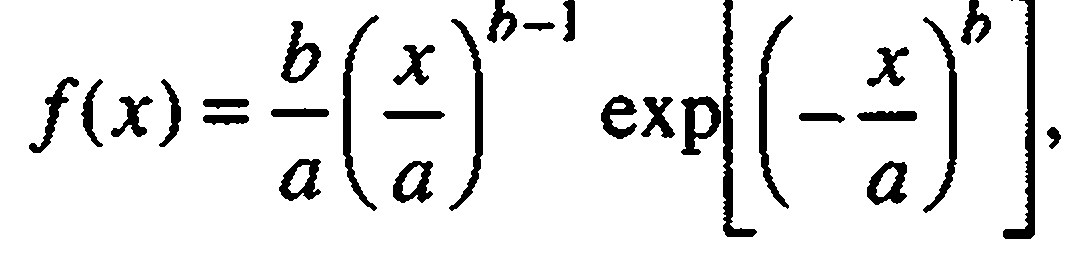У значительной части узлов и деталей процесс изменения технического состояния в зависимости от времени или пробега автомобиля носит плавный, монотонный характер, приводящий к возникновению так называемых постепенных отказов. При этом характер зависимости может быть различным.
1. Функция 1-го порядка
2. Степенная функция
Закономерность вариации случайных величин. Закономерность ТЭА второго вида.
При работе группы автомобилей приходится иметь дело не с одной зависимостью Y(t), которая была бы пригодна для всей группы, а с индивидуальными зависимостями Yi(t), свойственными каждому i-му изделию. Применительно к техническому состоянию однотипных изделии причинами вариации являются: даже незначительные изменения от изделия к изделию качества материалов, обработки деталей, сборки; текущие изменения условий эксплуатации (скорость, нагрузка, температура и т.д.); качество ТО и ремонта, вождения автомобилей и др. В результате при фиксации для группы изделий определенного параметра технического состояния, например Yп, каждое изделие будет иметь свою наработку до отказа, т.е. будет наблюдаться вариация наработки.
Оценки случайных величин
1. Случайные величины (от 1 до п) располагают в порядке возрастания или убывания их абсолютных значений: Х. = Xmin; Х2; Х3; Х4;...; Хi;...Хn-1;...; Хn = Хmах
2. Точечные оценки СВ:
среднее значение СВ
- среднее квадратичное
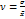- вариации
В ТЭА различают СВ:
· с малой вариацией: 
≤0;
· со средней вариацией: 0,1 ≤ ≤ 0,33;
· с большой вариацией: ≥ 0,33.
Нормальный закон распределения
Такой закон формируется, когда на исследуемый процесс и eгo результат влияет сравнительно большое число независимых (или слабозависимых) элементарных факторов (слагаемых), каждое из которых в отдельности оказывает лишь незначительное действие по сравнению с суммарным влиянием всех остальных.
Экспоненциальный закон
При экспоненциальном законе распределения вероятность безотказной работы не зависит от тoгo, сколько проработало изделие с начала эксплуатации, а определяется конкретной продолжительностью рассматриваемого периода или пробега Ах, называемого временем выполнения задания. Таким образом, эта модель не учитывает постепенного изменения параметров технического состояния, например, в результате изнашивания, старения и других причин, а рассматривает так называемые нестареющие элементы и их отказы. Экспоненциальный закон используется чаще всего при описании внезапных отказов, продолжительности разнообразных ремонтных воздействий и в ряде других случаев:
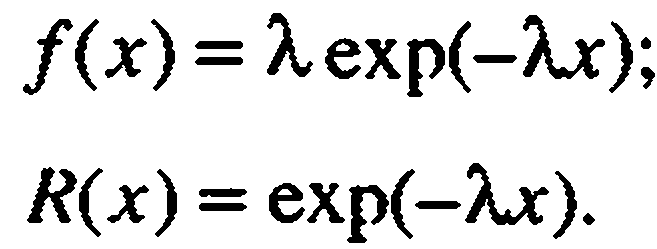
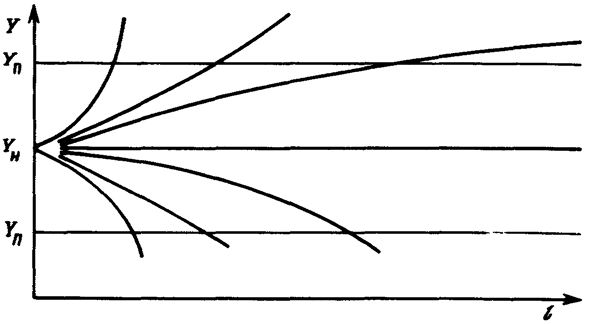
25 Закон распределения Вей6улла-Гнеденко
Проявляеться в модели так называемо слабого звена. Если система состоит из группы не зависимых элементов, отказ каждого из которых приводит к отказу всей системы, ТО в такой модели рассматривается распределение времени (или пробега) достижения предельного состояния системы как распределение соответствующих минимальных значений Х; отдельных элементов:
Хс = min(Xl; Х2;...; Хn) Функция распределения этой величины может быть выражена следующей зависимостью:
