КОНТРОЛЬНАЯ РАБОТА № 1.
Целью контрольной работы №1 является построение топографического плана по результатам геодезических измерений. Работа состоит из трех заданий, выполняемых в «Тетради для выполнения контрольной работы». Решение всех задач, входящих в данную работу, высылаются на рецензирование одновременно.
ЗАДАНИЕ 1. Вычисление исходных дирекционных углов; решение прямой геодезической задачи.
ЗАДАЧА 1.1. Вычислить дирекционные углы линий ВС и СД, если известен дирекционный линии АВ и измеренные правые по ходу углы β1 и β2 (см. рис.1).
Исходный дирекционный угол линии АВ берется в соответствии с шифром и фамилией студента: число градусов равно двузначному числу, состоящему из двух последних цифр шифра; число минут равно 30.2 плюс столько минут, сколько букв в фамилии студента.
Например: Зуев, шифр – 1101229, αАВ=29˚34.2΄.
Правый угол при точке В (между сторонами АВ и ВС) для всех вариантов равен, β1=189˚59.2΄; правый угол при точке С (между сторонами ВС и СД) для всех вариантов равен, β2 =159˚28.0΄.
Дирекционные углы вычисляют по правилу: дирекционный угол последующей стороны равен дирекционному углу предыдущей стороны плюс 180˚ и минус горизонтальный угол, справа по ходу лежащий.
Следовательно:
αВС = αАВ +180˚ - β1; αСD = αВС +180˚ - β2.
Пример. Вычисление дирекционных углов выполняем столбиком:
αАВ ……………………… 29˚34.2΄+
180˚
 |
209˚34.2΄ -
189˚59.2΄
 |
αВС……………………… 19˚35.0΄ +
 |
180˚
199˚35.0΄ -
 |
159˚28.0΄
αСD………………………40˚07.0΄
Примечание. Если при вычислении уменьшаемое окажется меньше вычитаемого, то к уменьшаемому прибавляем 360˚. Если дирекционный угол получается больше 360˚, то из него вычитают 360˚.
ЗАДАЧА 1.2. Решение прямой геодезической задачи.
Найти координаты Хс и Ус точки С (см. рис.1), если известны координаты точки В, равные Хв=-14.02 м, Ув=+627.98 м, длина (горизонтальное проложение) линии ВС, равное dвс=239.14 м и дирекционный угол линии ВС. Дирекционный угол линии ВС следует взять из решения предыдущей задачи.
Координаты точки С вычисляются по формулам: Хс=Хв+ΔХвс, Ус=Ув+ΔУвс, где ΔХвс и ΔYвс – приращения координат, вычисляемые из соотношений ΔXbc=dbc xcos α bc, ΔYbc=dbc x sin α bc.
Вычисление приращений координат рекомендуется вести на ПЭВМ или микрокалькуляторах. В этом случае знаки приращений координат устанавливаются в зависимости от знаков sin и cos.
Приращения координат можно вычислить предварительно переведя дирекционные углы в румбы, пользуясь табл.1. Тогда знаки вычисленных приращений координат определяют по названию румба, руководствуясь также табл.1.
Перевод дирекционных углов в румбы, знаки приращений координат. Таблица 1.
| Четверть | Формула перевода | Знаки приращений координат | ||
| Номер | название | ΔХ | ΔY | |
| I II III IV | СВ ЮВ ЮЗ СЗ | r = α r = 180˚ - α r = α - 180˚ r = 360˚ - α | + - - + | + + - - |
Пример. Дано dbc=239.14 м, αbc=19˚35΄.Выполнив вычисления, получаем Δ Xbc=+225.31 м и ΔYbc=+80.15 м.
Координаты точки С получаем алгебраическим сложением координат точки В с приращениями по линии ВС, действуя по схеме
Xc=Xb + ΔXbc=-14.02+225.31=+211.29 м,
Yc=Yb + ΔYbc=+627.98+80.15=+708.13 м.
Задачи решают в тетради, решение каждой из них должно сопровождаться схематичным чертежом, соответствующим выполняемому варианту.
В задаче 1.1 пример подобран так, что вычисленный дирекционный угол αсд последней линии должен получится на 10 ˚32.8΄больше, чем исходный дирекционный угол αав. Это должно служить контролем правильности решения задачи 1.1.
Решение задачи 1.2 непосредственно не контролируется. К ее
решению необходимо подойти особенно внимательно, так как вычисленные координаты точки С будут использоваться в задании 2.
ЗАДАНИЕ 2. Составление топографического плана строительной площадки.
По данным полевых измерений выполнить обработку и вычертить топографический план строительной площадки в масштабе 1:2000 с высотой сечения рельефа 1 м.
ИСХОДНЫЕ ДАННЫЕ.
1. Для съемки участка на местности между двумя пунктами полигонометрии ПЗ8 и ПЗ19 проложен теодолитно-высотный ход. В нем измерены длины всех сторон (рис. 2), а на каждой вершине хода – правый по ходу горизонтальный угол и углы наклона на предыдущую и последующую вершины. Результаты измерений горизонтальных углов и длин линий даны в табл.2, а результаты тригонометрического нивелирования даны в табл.4 и 4а. Эти данные являются общими для всех вариантов. Измерение углов проводилось оптическим теодолитом 2Т30 с точностью отчетов 0.5΄.
Результаты измерений углов и длин сторон.
Таблица 2.
| № вершин | Измеренные углы (правые) | Длины сторон (гор. Проложения), в м. | |
| ˚ | ΄ | ||
| ПЗ8 | 59.2 | ||
| 58.5 | 263.02 | ||
| 20.0 | 239.21 | ||
| 02.8 | 269.80 | ||
| ПЗ19 | 08.2 | 192.98 |




|

|
2. Известны координаты полигонометрических пунктов ПЗ8 и ПЗ19 (т.е. начальной и конечной точек хода): Xпз8=-14.02 м, Yпз8=+627.98 для всех вариантов; Xпз19 принимается равным Xc, а Yпз19-значению Yc, полученные при решении задачи 2 в задании 1.
Известны также исходный αо и конечный αn дирекционные углы:
αо – дирекционный угол направления ПЗ7 – ПЗ8 берется в соответствии с шифром и фамилией студента также, как и в задании 1. Таким образом αо = αав;
αn - дирекционный угол стороны ПЗ19 – ПЗ20 для всех студентов принимается равным дирекционному углу линии CD, вычисленному в задача 1, т.е. αn =αcd. Так в нашем примере αо = αав =29˚34.2΄, αn =αcd =40˚07.0΄.
3. Отметки пунктов ПЗ8 и ПЗ19 были получены из геометрического нивелирования. При выполнении же задания значение отметки ПЗ8 следует принять условно: количество целых метров в отметке должно быть трехзначным числом, в котором количество сотен метров равно единице, а количество десятков и единиц метров составляют две последние цифры шифра студента. В дробной части отметки (дм, см, мм) ставятся те же цифры, что и в целой части например: Зуев – шифр – 1101229, то отметка пункта ПЗ8 будет равна 129.129 м. Отметка ПЗ19 для всех студентов принимается на 3.282 м больше отметки ПЗ8.
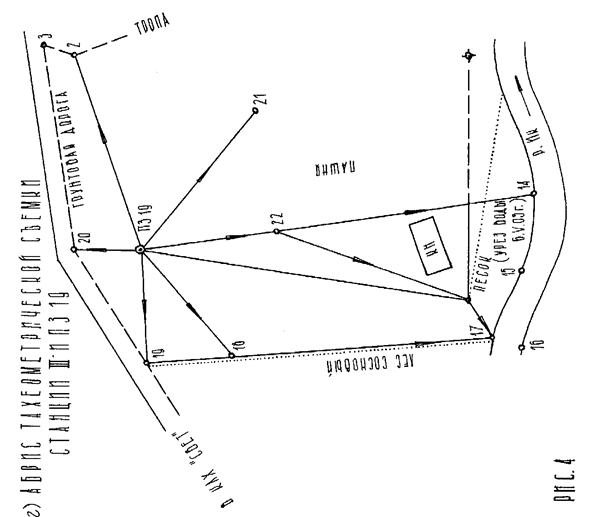
4. При съемке участка местности были составлены абрисы съемки, показанные на рис. 3, а и б, и рис. 4, а-г.
УКАЗАНИЯ К ВЫПОЛНЕНИЮ РАБОТЫ.
Обработка ведомости вычисления координат вершин хода.
1.1. Увязка угловых измерений.
Значения измеренных углов записывают в графу 2 ведомости вычисления координат (см. табл.3). В графе 4 записывают и подчеркивают исходный дирекционный угол αо на верхней строчке и конечный дирекционный угол αn на нижней строчке. Вычисляют сумму измеренных углов хода Σβпр. Определяют теоретическую сумму углов по формуле: Σβт = αо – αn +180˚ х n, здесь n – число вершин хода.
Находим угловую невязку: fβ = Σβпр – Σβт.
Если невязка fβ не превышает допустимой величины: fβ доп.=1΄х √n, то ее распределяют с обратным знаком поровну на все углы хода с округлением значений поправок до десятых долей минуты. Исправленные этими поправками углы записывают в графу 3 ведомости, Сумма исправленных углов должна равняться теоретической сумме.
1.2. Вычисление дирекционных углов и румбов сторон хода.
По исходному дирекционному углу αо и исправленным значениям углов β хода по формуле для правых углов вычисляют дирекционные углы всех остальных сторон: дирекционный угол последующей стороны равен дирекционному углу предыдущей стороны плюс 180˚ и минус правый исправленный угол хода, образованный этими сторонами.
Например: αпз8-1 = αо + 180˚ - βпз8 =29˚34.2΄ + 180˚ + 360˚ - 330˚58.9΄=238˚35.3΄.
Для контроля вычисления дирекционных углов следует найти конечный дирекционный угол αn по дирекционному углу α111-пз19 последней стороны и исправленному углу βпз19 (см. рис.2):
αn = α111-пз19 + 180 – βпз19.
Это вычисленное значение αn должно совпасть с заданным дирекционным углом αn. При переходе от дирекционных углов к румбам см. табл.1.
Значения дирекционных углов записывают в графу 4 ведомости с точностью до десятых долей минут, а румбов – в графу 5, при этом
значения румбов округляют до целых минут.
1.3 Вычисление приращений координат.
Приращения координат вычисляют по формулам:ΔX =d x cos α=d x cos r; ΔY = d x sin α = d x sin r; так же, как в задаче 2 задания 1.
Вычисленные значения приращений координат ΔX и ΔY выписывают в графу 7 и 8 ведомости с точностью до сотых долей метра. Знаки приращений координат устанавливают в зависимости от знаков sin α и cos α, либо по названию румба, руководствуясь табл.1. В каждой из граф складывают все вычисленные значения ΔX и ΔY, находя практические суммы приращений координат Σ ΔXпр и Σ Δyпр.
1.4. Нахождение абсолютной и относительной линейных невязок хода; увязка приращений координат.
Сначала вычисляют невязки fx и fy в приращениях координат по осям x и y: fx = Σ ΔXпр - Σ ΔXт; fy = Σ Δyпр - Σ Δyт; где Σ ΔXт = Xкон. – Xнач., Σ Δyт = Yкон. – Yнач. Теоретические суммы приращений координат вычисляются как разность абсцисс и ординат конечной ПЗ19 и начальной ПЗ8 точек хода. Координаты начальной и конечной точек хода записывают в графах 11 и 12 и подчеркивают.
Абсолютную линейную невязку ΔР хода вычисляют по формуле:
ΔР = √ f ²x + f ²y и записывают с точностью до сотых долей метра.
Относительная линейная невязка ΔР/Р хода (Р - сумма длин сторон хода) выражается простой дробью с единицей в числителе. Если относительная невязка окажется меньше допустимой 1/2000, то невязки fx и fy распределяют, вводя поправки в вычисленные приращения координат. Поправки в приращения распределяют прямо пропорционально длинам сторон, записывают в графе 6, и вводят со знаком, обратным знаку соответствующей невязки. Значения поправок округляют до сотых долей метра и записывают в ведомости над соответствующими приращениями, следя за тем, чтобы суммы поправок в ΔX и Δy равнялись соответственно невязкам fx или fy с противоположным знаком. Исправленные приращения координат записывают в графы 9 и 10; суммы исправленных приращений координат должны быть равны соответственно Σ ΔXт и Σ Δyт.
Пример в задании подобран так, чтобы невязка ΔР/Р получилась допустимой. Если эта величина окажется больше 1/2000, значит в вычислениях допущена ошибка. Чаще всего ошибки встречаются при вычислениях дирекционных углов, при переводе дирекционных углов в румбы, в знаках приращений и при вычислении приращений.






