Математический анализ
1. Предел числ. Посл. – если по некоторому закону каждому натуральному числу n поставлено в соответствие определенное число an то говорят, что задана числ.послед. {an} a1, a2…an. Где а1, а2 – члены числ.послед., ап - общий чл.ч.пос.
2. Число а наз. Пределом функции y=f(x), при х→∞, если для любого сколь угодно малого положительного Е найдется такое число М, зависящее от Е(М/Е>0), то для всех значений х таких, что │х│>М справедливо неравенство │F(x)-A│>E.
3. Число А называется пределом функции y=f(x),при х→х0(или в точке х0), если для любого сколь угодно малого положит. Е найдется такое число δ, зависящее от Е, что для все значений х, не равных х0, таких, что │х-х0│>δ справедливо неравенство │F(x)-A│<Е.
4. 1. Функция y=α(x) называется бесконечно малой величиной при x→x0
(или при x → ∞), если ее предел равен нулю.
2. Если функция f (x) при x → a имеет предел, равный А, то ее можно представить в виде суммы предела A и бесконечно малой α (x) при x → a
F(x)=A+α(x).
Алгебр.сумма конечного числа БМВ есть величина бесконечно малая;
Произведение БМВ на ограниченную функцию (в том числе на остоянное число или на др.БМВ)есть величина бесконечно малая;
Частное от деления БМВ на функцию, предел которой отличен от 0 есть величина бесконечно малая.
6. Функция y=F(x)называется бесконечно большой величиной при x→x0(или при x → ∞), если для любого, сколь угодно большого положит. Числа M, найдется такое положит. δ (зависящее от M), что для всех значений х≠х0 и удовлетворяющих условию │х-х0│<δ справедливо неравенство │F(x)│>М.
Св-ва: 1. Произведение ББВ на функцию, предел которой отличен от 0 есть величина бесконечно большая;
Сумма ББВ и ограниченной функции есть величина беск.большая;
3. частное от деления ББВ на функцию, имеющую предел в точке х0 есть величина бесконечно большая..
7. Если α (x) – БМВ, при х→х0 или х→∞ и при этом α(х)≠0, тогда 
-ББВ при х→х0или при х→∞.
Если f(x)-ББВ, при х→х0 или х→∞, тогда α(х)= 
- БМВ при х→х0 или х→∞.
8. единственность предела функции. Функция не может иметь в одной точке два различных предела.
предел суммы двух функции. Предел алгебраической суммы конечного числа функций равен такой же сумме пределов этих функций, т.е. lim(f(x)+q(x))=A+B, (х→х0 или х→∞)
предел произведения конечного числа функций равен произведению пределов этих функций, т.е. lim(f(x)*q(x))=A+B (x→x0 или х→0).
Постоянный множитель можно вынести за знак предела, т.е. lim C*f(x)=C*A,(С-const, х→х0 или х→∞)
Предел частного двух функций равен частному пределов этих функций, при условии, что предел знаменателя не равен 0, т.е. lim 
= 
(В≠0) (х→х0 или х→∞).
Предел сложной функции. Если lim f(u)=A (u→u0), и limϕ(x)=U0(x→x0), тогда предел сложной функции будет: limf(ϕ(x))=A(x→x0).
Если в некоторой окресности точки х0 или при достаточно больших значениях х справедливо f(x)<q(x), тогда limf(x)≤limq(x) (х→х0 или х→∞).
9. 1-ый замечат.предел справедливо равенство: lim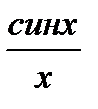 
=1(x→0)
10. Число e явл. пределом следующей последовательности: lim(1+ 
)n=e (n→∞)
11. Функция y=f(x) называется непрерывной в точке х0, если выполняются три условия:1.функция определена в точке х0, т.е. существует значение f(x); 2. функция имеет предел в точке х0, т.е. сущ. Предел f(x), при х→х0; 3. Этот предел равен значению функции, т.е. lim f(x)=f(x0), (x→x0).
12. Св-ва непр. ф в точке 1.Если функция F(x) и q(x) непрерывна в точке x0, тогда f(x)±q(x); f(x)*q(x); 
(q(x0)≠0)тоже непрерывны в точке x0 2.Если функция f(x) непрерывна в точке х0 и f(x0)>0, тогда найдется такая окрестность в точке х0, в которой f(x)>0. Если f(x0)<0 аналогично. 3. Если y=f(u) непрерывна в точке у0 и функция и=ϕ(х) непрерывна в х0, тогда сложная функция у=f(ϕ(x)) непрерывна в х0.
13. Св-ва непр. На отрезке ф. 1. Если y=f(x) непрерывна на отрезке [а;в], тогда она ограничена на этом отрезке, т.е. найдется такое полож.число М, что для всех значений х из отрезка [а;в], f(x)≤M. 2. Если функция у=f(x)непрерывна на отр.[a;b], то она достигает на этом отрезке своего наименьшего значения m и наибольшего значения M. 3. Если функция у=f(x) непрерывна на отрезке [a;b] и принимает значения разных знаков на концах этого отрезка, тогда внутри отрезка найдется хотя бы одна такая точка СЄ(а;в), что f(c)=0.
14. Производной ф. у=f(x) в точке х0 наз.предел отношений приращения функции к приращению аргуманта, когда приращение аргумента →0, если этот предел существует и конечен,т.е. у,=lim 
(x→0) или f/=lim 
(∆x→0)
Физ.смысл производной: если мы обозначим S(t)- функцию пути от времени, тогда v прямолинейного движения в любой момент времени t будет равна v(t)=S/(t)
Геометрический смысл производной: Производная в точке x0 равна угловому коэффициенту касательной к графику функции y = f(x) в этой точке. K=f/(x0).
15. Теорема. Если функция при некотором значении аргумента х0 имеет производную, то она непрерывна в этой точке х0,
