Москва, 2014
Содержание
Введение. 3
Методика разработки экспертной системы.. 9
Вывод. 23
Введение
Перед тем, как перейти непосредственно к методике разработки экспертной системы, необходимо сказать несколько слов о контент-анализе.
Контент-анализ – количественный анализа текстов и текстовых массивов с целью последующей содержательной интерпретации выявленных числовых закономерностей. Основная идея контент-анализа проста и интуитивно наглядна.
При восприятии текста и особенно больших текстовых потоков мы достаточно хорошо ощущаем, что разные формальные и содержательные компоненты представлены в них в разной степени, причем эта степень по крайней мере отчасти поддается измерению: ее мерой служит то место, которое они занимают в общем объеме, и/или частота их встречаемости.
Замысел контент-анализа заключается в том, чтобы систематизировать интуитивные ощущения, сделать их наглядными и проверяемыми и разработать методику целенаправленного сбора тех текстовых свидетельств, на которых эти ощущения основываются. При этом предполагается, что вооруженный такой методикой исследователь сможет не просто упорядочить свои ощущения и сделать свои выводы более обоснованными, но даже узнать из текста больше, чем хотел сказать его автор. Скажем, настойчивое повторение в тексте каких-то тем или употребление каких-то характерных формальных элементов или конструкций может не осознаваться автором, но обнаруживает и определенным образом интерпретируется исследователем - отсюда принадлежащее социологу
А. Г. Здравомыслову полушутливое определение контент-анализа как «научно обоснованного метода чтения между строк».
Реально главной отличительной чертой контент-анализа является не его декларируемая во многих определениях «систематичность» и «объективность» (эти черты присущи и другим методам анализа текстов), а его квантитативный (количественный) характер. Контент-анализ – это прежде всего количественный метод, предполагающий числовую оценку каких-то компонентов текста, дополняющийся также различными качественными классификациями и выявлением тех или иных структурных закономерностей.
Поэтому наиболее удачным определением контент-анализа можно считать то, которое зафиксировано в относительно недавней книге Мангейма и Рича: контент-анализ – это систематическая числовая обработка, оценка и интерпретация формы и содержания информационного источника.
В качестве примера приведем стихотворение А.С.Пушкина «Памятник»:
Я памятник себе воздвиг нерукотворный,
К нему не зарастет народная тропа,
Вознесся выше он главою непокорной
Александрийского столпа.
Нет, весь я не умру — душа в заветной лире
Мой прах переживет и тленья убежит —
И славен буду я, доколь в подлунном мире
Жив будет хоть один пиит.
Слух обо мне пойдет по всей Руси великой,
И назовет меня всяк сущий в ней язык,
И гордый внук славян, и финн, и ныне дикой
Тунгус, и друг степей калмык.
И долго буду тем любезен я народу,
Что чувства добрые я лирой пробуждал,
Что в мой жестокий век восславил я свободу
И милость к падшим призывал.
Веленью божию, о муза, будь послушна;
Обиды не страшась, не требуя венца,
Хвалу и клевету приемли равнодушно
И не оспоривай глупца.
Стихотворение А.С. Пушкина «Я памятник воздвиг себе нерукотворный…» (1836) представляет собой своеобразное поэтическое завещание поэта. По теме оно восходит к оде римского поэта Горация «К Мельпомене», откуда взят и его эпиграф. Интересно, что первый перевод этой оды был сделан М. В. Ломоносовым, затем ее основные мотивы развивал Г. Р. Державин в своем стихотворении «Памятник» (1796). Но все эти поэты, подводя итог творческой деятельности, различно оценивали свои поэтические заслуги и смысл творчества, по-разному формулировали свои права на бессмертие. Гораций считал себя достойным славы за то, что хорошо писал стихи, Державин — за поэтическую искренность и гражданскую смелость.
Он говорит о себе не только как о национальном русском поэте, оставившем след в памяти народной. Он уверен, что к его памятнику «не зарастет народная тропа». Поэт как бы очерчивает географические границы своей славы, пророчески предсказывает, что его поэзия станет достоянием всех народов России:
Слух обо мне пройдет по всей Руси великой,
И назовет меня всяк сущий в ней язык,
И гордый внук славян, и финн, и ныне дикой
Тунгус, и друг степей калмык.
Больше того, в этом стихотворении лирический герой, с ясным осознанием своего права, выражает надежды на бессмертие:
Нет, весь я не умру — душа в заветной лире
Мой прах переживет и тленья убежит...
Концовка стихотворения представляет собой традиционное обращение поэта к Музе. По мнению Пушкина, Муза должна быть «послушна» только «веленью Божию», то есть голосу внутренней совести, голосу правды. Она должна следовать собственному высокому предназначению, не обращая внимания на «хвалу и клевету» невежественных глупцов.
Стихотворение богато средствами художественной выразительности. В частности, здесь довольно много эпитетов: «заветная лира», «Русь великая», «друг степей калмык», «подлунный мир». Кроме того, произведение насыщено метафорами: «душа в заветной лире», «душа мой прах переживет и тленья убежит» и другие. Есть здесь и олицетворения: «хвалу и клевету приемли равнодушно И не оспоривай глупца». Также в стихотворении присутствует гипербола: «и славен буду я, доколь в подлунном мире жив будет хоть один пиит»; метонимия: «и назовет меня всяк сущий в ней язык», «слух обо мне пройдет по всей Руси великой».
Таким образом, стихотворение «Я памятник воздвиг себе нерукотворный…» представляет собой образец зрелой лирики поэта, в которой он выражает отношение к проблеме поэта и поэзии, а также к собственному творчеству, к собственной творческой судьбе.
Такой литературоведческий анализ несомненно содержит элемент субъективизма, и он также не позволяет дать необъективную сравнительную оценку этого стихотворения с произведениями других поэтов.
Покажем, что такие несубъективные оценки можно производить с помощью информационных измерений.
Известно, что впервые числовые оценки поэтического текста выполнялись известным русским математиком Марковым А.А. в начале ХХ столетия. Сущность этих оценок сводилась к следующему: из романа Пушкина А.С. «Евгений Онегин» составлялся список всех слов, например, на начальную букву «а», затем, исходя из этого списка, подсчитывалась вероятность появления всех букв русского алфавита на втором месте после буквы «а», далее на третьем месте и т.д. По такой же схеме анализировались списки слов на другие начальные буквы.
Вероятностный процесс появления букв алфавита в определенных позициях слова Марков А.А. назвал случайным процессом, начинающимся с некоторого начального состояния. В указанном случае начальное состояние – это список слов на начальную букву «а».
В настоящее время в теории массового обслуживания такие случайные процессы стали называться цепями Маркова.
Итак, нашей задачей является построение экспертной системы для оценки поэтических текстов А.С.Пушкина. Для ее построения за основу возьмем исследования поэта Юрия Кузнецова.
Поэт Юрий Кузнецов в своем творчестве следовал традициям русской поэзии, в своих размышлениях о русской поэзии выделил в них 2 характерные темы:
1. любовная череда, начатая Пушкиным;
2. дорожная череда, начатая Лермонтовым.
Он выбрал следующие стихотворения:
| № | Название | Автор |
| 1. | «Я помню чудное мгновенье» | Пушкин А.С. |
| 2. | «Средь шумного бала» | Толстой Л.Н. |
| 3. | «К.Б.» | Тютчев Ф.И. |
| 4. | «Сияла ночь» | Фет А.А. |
| 5. | «Незнакомка» | Блок А.А. |
| 6. | «За дорожной случайной беседой» | Кузнецов Ю.Н. |
| 7. | «Выхожу один я на дорогу» | Лермонтов М.Ю. |
| 8. | «Тройка» | Некрасов Н.А. |
| 9. | «Накануне годовщины» | Тютчев Ф.И. |
| 10. | «Осенняя воля» | Блок А.А. |
| 11. | «Распутье» | Кузнецов Ю.Н. |
Для этих текстов были вычислены следующие показатели: Н1, Н2, ∆, S и λ1, λ2, λ3.
| Энтропия поэтических текстов | |||||||
| № | Н1 | Н2 | ∆ = Н1-Н2 | S | λ1 | λ2 | λ3 |
| 1. | 4,0163 | 4,4958 | 0,4795 | 4,8 | 3,1 | 92,1 | |
| 2. | 3,9922 | 4,5610 | 0,5688 | 4,3 | 99,6 | 89,6 | |
| 3. | 3,2041 | 4,3764 | 1,1724 | 4,4 | 3,1 | 89,8 | 90,9 |
| 4. | 4,0219 | 4,5122 | 0,4903 | 4,0 | 97,6 | 92,2 | |
| 5. | 4,0503 | 4,5093 | 0,4590 | 5,1 | 91,1 | ||
| 6. | 4,0407 | 4,4605 | 0,4197 | 4,6 | 3,6 | 91,4 | 93,5 |
| 7. | 4,0871 | 4,5144 | 0,427 | 4,2 | 1,1 | 91,1 | |
| 8. | 3,9837 | 4,5853 | 0,601 | 5,1 | 3,7 | 90,6 | 90,5 |
| 9. | 3,7151 | 4,3921 | 0,677 | 4,2 | 1,5 | 95,4 | |
| 10. | 4,0756 | 4,5543 | 0,479 | 4,8 | 1,1 | 94,4 | |
| 11. | 3,9345 | 4,3805 | 0,446 | 4,5 | 1,1 | 89,8 |
Были выделены эталонные показатели:
4 ≤ Н1 ≤ 4,1
0,4 ≤ ∆ ≤ 1,2
4 ≤ S ≤ 5,1
1 ≤ λ1 ≤ 3,7
90 ≤ λ2 ≤ 100
90 ≤ λ3 ≤ 96
Далее были отобраны стихотворения, подходящие под эталонные показатели:
| № | Название | Н1 | Н2 | ∆ = Н1-Н2 | S | λ1 | λ2 | λ3 |
| 1. | «Я помню чудное мгновенье» Пушкин А.С. | 4,0163 | 4,4958 | 0,4795 | 4,8 | 3,1 | 92,1 | |
| 4. | «Сияла ночь» Фет А.А. | 4,0219 | 4,5122 | 0,4903 | 4,0 | 97,6 | 92,2 | |
| 5. | «Незнакомка» Блок А.А. | 4,0503 | 4,5093 | 0,4590 | 5,1 | 91,1 | ||
| 7. | «Выхожу один я на дорогу» Лермонтов М.Ю. | 4,0871 | 4,5144 | 0,427 | 4,2 | 1,1 | 91,1 | |
| 10. | «Осенняя воля» Блок А.А. | 4,0756 | 4,5543 | 0,479 | 4,8 | 1,1 | 94,4 |
Методика разработки экспертной системы
После исследований, проведенных русским математиком Марковым А.А. в начале XX столетия, интерес к информационным изменениям текстов естественного языка возобновился только с установлением Шенноном следующей формулы для вычисления количественной меры информации:
 , (1)
, (1)
где Pi – вероятность или частота i-ого события.
В своей работе мы также используем данные показатели.
Pi – это показатель субъективной оценки поэтических текстов. С позиции исчисленской части языка любой текст – это множество слов. Слова образуют группы слов по какому-либо признаку. В качестве такого признака можно выбрать, например, начальную букву слова. Если число всех слов в тексте обозначить через Ni, а число слов на конкретную начальную букву – через ni, то можно определить величину Pi.
 (2)
(2)
Для того, чтобы подсчитать ni, мы в ячейку F2 вставляем формулу «СЧЕТЕСЛИ» из категории «Статистические». Диапазон указывается «В:В» (английский регистр), условие «Е2», затем размножаем формулу до конца таблицы (см. рис.1.).

Рис.1.
Для подсчета Ni в ячейку E30 вводится «N =», а в ячейку F30 вставляется формула суммы всех букв. Для этого щелкаем на этой ячейке и затем по кнопке «Автосумма»  , и нажимаем клавишу «Enter» на клавиатуре. В итоге получается следующая таблица (см. рис.2):
, и нажимаем клавишу «Enter» на клавиатуре. В итоге получается следующая таблица (см. рис.2):

Рис.2.
Далее возвращаемся к нашей формуле (2) и считаем Pi. В ячейку G2 ввести «=F2/F$30», а затем размножить до конца таблицы. В результате в столбце G получим значение Pi (см. рис.3.).
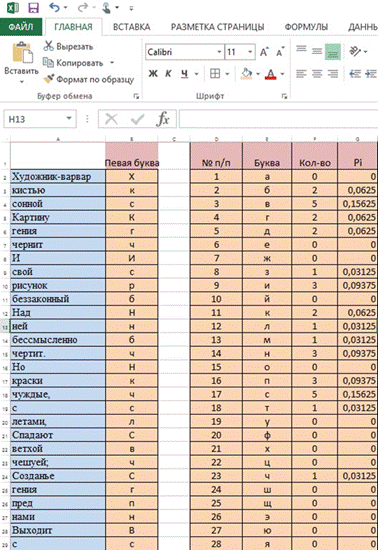
Рис.3.
Вернемся к формуле (1). Величина Hi измеряется в битах и ее часто называют энтропией информации. Формулу (1) стали применять при анализе кодов, используемых при передаче сообщений, составленных на каком-либо естественном языке.
Для подсчета H1 в ячейку H2 вводим
«=ЕСЛИ (G2=0;0;-G2*Log(G2;2))», что соответствует формуле (1), а затем размножаем до конца таблицы. В ячейку G30 вводим «Н =». В ячейку Н30 вставляем формулу автосуммы  (см. рис.4.).
(см. рис.4.).

Рис. 4.
Анализ таблицы, приведенный ниже показывает, что количественная мера информации Н1 различна для каждого произведения, и ее числовые значения для стихотворений Пушкина изменяются в пределах от 1,5849 до 3, 5786 (см. рис.5.).
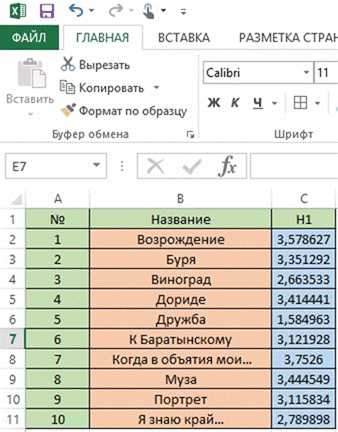
Рис.5.
Для проведения несубъективного анализа необходимо еще посчитать несколько показателей. Одним из них является N2.
N2 – показывает общее количество букв в тексте. Для нахождения этого показателя мы подсчитали количество всех букв, начиная с «а», в стихотворении и перенесли данные в таблицу.
Для этого нужно в меню « Правка » выбрать команду « Заменить ». В окне диалога « Заменить » после слова «Найти» пишем «а» и щелкаем по кнопке « Заменить все ». Программа сообщает нам, сколько произведено замен. Это число 20 и есть количество букв «а» в тексте (см. рис.6.).

Рис. 6.
Заносим количество букв «а» с клавиатуры в таблицу, в ячейку L2. Проделываем эту операцию с остальными буквами, после чего столбец L окажется полностью заполненным (см. рис.7.).

Рис.7.
Далее в MS Excel проводим подсчет всех букв в стихотворении. Для этого щелкаем по ячейке L35. В меню «Вставка» выбираем команду «СУММ» и щелкаем по кнопке «ОК», для перехода к шагу 2. В появившемся окне « Аргументы функции » напротив надписи « Число 1 » набираем с клавиатуры или выделяем мышкой диапазон ячеек L2:L34 и щелкаем по кнопке «ОК». В результате чего в ячейке L35 оказалось число 261, равное числу всех букв в тексте стихотворения. В ячейку K35 вводим с клавиатуры «N2 =», так как число букв нами обозначено через N2 (см. рис.8.)

Рис. 8.
Также в анализе необходимо посчитать показатель Н2. Он вычисляется с помощью функции ЕСЛИ и формулы Шеннона:

Для этого в ячейке N2 мы вводим следующую формулу: «=ЕСЛИ(M2=0;0;-M2*LOG(M2;2))» и растягиваем до ячейки N34. Затем в ячейку M35 вносим обозначение энтропии «Н2 =», а в ячейке N35 суммируем диапазон ячеек N2:N34 с помощью функции автосуммы  (=СУММ(N2:N34)). Получаем следующую таблицу (см. рис.9.):
(=СУММ(N2:N34)). Получаем следующую таблицу (см. рис.9.):

Рис. 9.
Так как в ходе проводимого нами анализа удалось выявить тексты, для которых H1 и H2 близки, мы вводим новый критерий ∆ = Н2-Н1 (см. рис.10.).
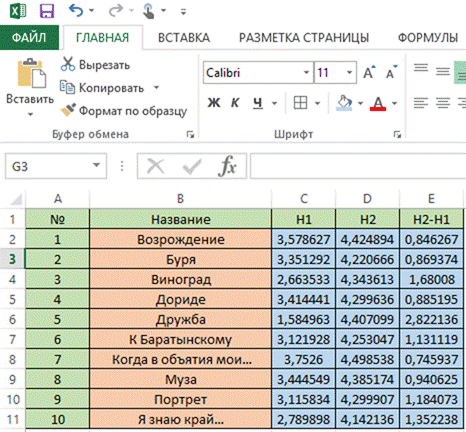
Рис. 10.
Далее определим среднее количество букв в слове, обозначим этот показатель как S.
S = N2/N1,
где N2 – общее количество букв в стихотворении;
N1 – общее количество слов в стихотворении.
Минимальное значение составляет 1,28 («К Баратынскому…» а максимальное 5,83 («Виноград»). Этот показатель оказывает непосредственное влияние на показатель уровня образования (λ1) (см. рис.11).

Рис. 11.
Учебный текст должен быть удобочитаем и понимаем. В настоящее время имеется ряд исследований, в которых предложены математические модели анализа сложности текстов вообще и учебных текстов с учетов возрастных особенностей учащихся, в частности. Однако, с одной стороны, эти модели получены, преимущественно для английских текстов, а с другой, не подкреплены соответствующими системами автоматизированного анализа с практичным и удобным интерфейсом. Между тем, потребность в такого рода системах и соответствующих методиках анализа текстов существует не только у экспертов-методистов федерального или регионального уровней, но и у создателей учебников и методик, у учителей, разрабатывающих различные дидактические материалы.
Подпрограмма «Статистика удобочитаемости» показывает общие средние количества символов, слов и предложений, а также позволяет оценить показатели легкости чтения текста. Эти показатели характеризуют текст с точки зрения того, насколько должен быть подготовлен читатель для его восприятия (см. рис.12).
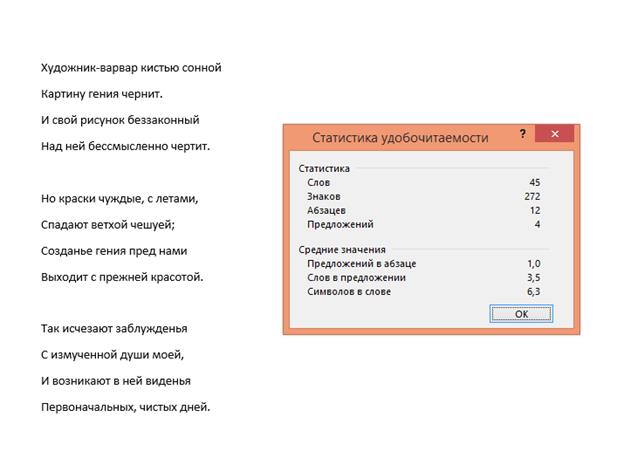
Рис. 12.
λ1 – уровень образования, основан на образовательном индексе Флеша-Кинсайда и показывает, каким уровнем образования должен обладать читатель исследуемого текста. Подсчет делается на основе вычисления среднего числа слогов в слове и слов в предложении.
Значения показателя от 0 до 20:
· от о до 10 – число классов школы, оконченных читателем;
· от 11 до 15 – курсы высшего учебного заведения;
· от 16 до 20 – относятся к сложным научным текстам.
Эталонным считаются от 1 до 3,7.
Рассчитывается по формуле:
λ1 = (0,39 * СДП) + (11,8 * СЧС) – 15,59,
где СДП – средняя длина предложения (= число слов в документе/число предложений);
СЧС – среднее число слогов в документе (= число слогов в документе/число слов).
λ2 – легкость чтения, подсчитывается по среднему числу слогов в слове и слов в предложении. Чем выше значение, тем легче прочесть текст и тем большему числу читателей он будет понятен.
Варьируется от 0 до100. Рекомендуемый интервал значений - от 60 до 70.
Рассчитывается по формуле:
λ2 = 206,835 – (1,015 * СДП) – (84,6 * СЧС)
λ3 – благозвучие, указывает на удобочитаемость текста с фонетической точки зрения. Подсчет основан на вычислении среднего количества шипящих и свистящих согласных.
Интервал изменения показателя – от 0 до 100. Рекомендуемый диапазон значений – от 80 до 100.

Рис. 13.
Вывод
Проведя с помощью созданной нами экспертной системы несубъективный литературоведческий анализ, сравним полученные значения со значениями эталонных произведений, приведенных во введении:
· среднее арифметическое количество букв в словах текста S должно варьироваться в пределах от 4 до 5,1;
· энтропия Н1 – в пределах от 4 до 4,1;
· значение показателя ∆ - от 0,4 до 1,2;
· уровень образования λ1- от 1 до 3,7;
· легкость чтения λ2 – от 90 до 100;
· благозвучие λ3 – от 90 до 96.
Проанализировав 10 произведений А.С.Пушкина, мы отобрали 4, которые отвечают эталонных значениям (стихотворения 2,3,9,10) 
Рис. 14.






