Переходной процесс строится для замкнутой системы. Для этого вводится отрицательная обратная связь. Если запасы устойчивости по фазе и по амплитуде удовлетворяют всем требованиям, предъявляемым в техническом задании, то достаточно ввести единичную обратную связь (коэффициент передачи равен 1). Если требования не выполнены – необходимо введение дополнительных корректирующих звеньев.
Передаточную функцию замкнутой системы определим как
где: K ос – коэффициент передачи цепи обратной связи.
= 
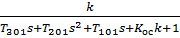. (36)
Примем K ос=1.
Выполним обратное преобразование Лапласа и тем самым, перейдем во временную область
Используя ППП Matlab и команду step() получим переходной процесс исследуемой системы. Используя возможности данной команды, и применив дополнительные параметры, отобразим на переходном процессе необходимые критерии для оценки качества переходного процесса:
· setting time – время переходного процесса;
· peak response – максимальное перерегулирование (величина перерегулирования и время достижения первого максимума);
· rise time – время нарастания;
· steady state – величина устранившегося значения после переходного процесса.
Также величину перерегулирования можно определить следующим образом
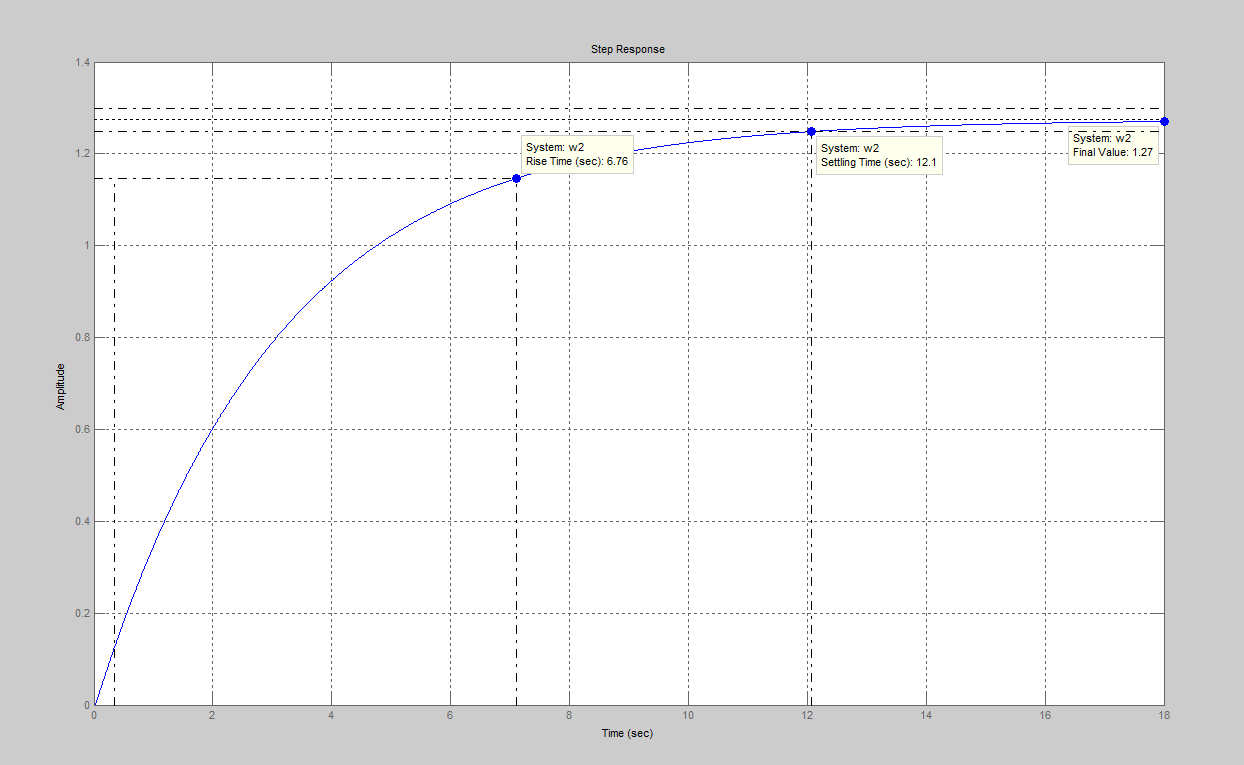
Рис. 8. Переходной процесс с единичным коэффициентом усиления Кос в цепи обратной связи
Используя полученный график переходного процесса, оценим качество переходного процесса по следующим критериям:
· время переходного процесса – t п=0,187 с; (t п=0,3 с)
· величина перерегулирования – σ =28,4%; (σ =30%)
· время нарастания – t н=0,0351 с; (t н=0,05 с)
· время запаздывания – t з=0,01 с; (t з=0,01 с).
Сравнивая полученные данные и данные, записанные в техническом задании (записаны в скобках) видно, что качество полученного переходного процесса удовлетворяет всем требованиям, предъявляемым к данной системе автоматического регулирования.
Приложение
Ниже представлен код программы, написанный с использованием MATLAB для построения характеристик исследуемой системы.
close all;
clc;
clear all;
T10=3.558;
T20=0.096;
T30=0.00065;
k=1.46;
p=tf('p')
w=k/(T30*p^3+T20*p^2+T10*p+1)
figure;
nyquist(w);
pole(w);
figure;
bode(w);
sisotool(w);
w2=w/(1+0.1*w);
figure;
step(w2);
Литература
1. Моргунов Г.М., Попов А.М. Управление техническими системами: комплексные лабораторные работы. Методическое пособие. МЭИ, 2004. – 32с.
2. Моргунов Г.М., Хачатуров М.М., Заверский М.М. Сборник задач по курсу теория автоматического регулирования. МЭИ, 1982. – 68 с.
3. Попов Д.Н. Динамика и регулирование гидро- и пневмосистем. Машиностроение, 1987. – 464 с.
