Тема. Вычисление первообразных. Метод замены переменной в подынтегральном выражении.
Занятие 5.
Рассмотрим дифференциал функции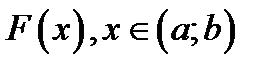 
: 
. Если 
является первообразной для функции 
, то 
. Первообразная функция 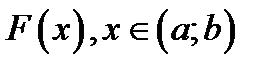для функции 
обозначается символом 
. Операция нахождения первообразной называется неопределённым интегрированием. Следующие записи эквивалентны
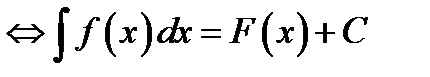. (5.1)
При вычислении неопределённого интеграла используются свойства:
1) 
.
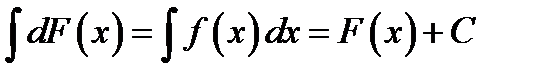2) инвариантности интегрирования:
Если 
, то 
,где 
любая дифференцируемая переменная, а также правила интегрирования:
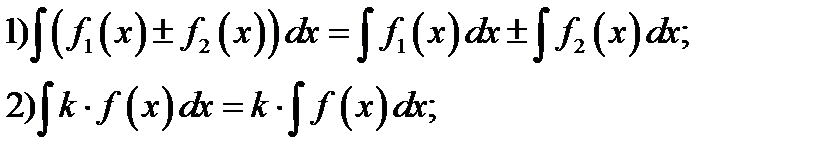(5.2)
Для проверки правильности полученного результата используют свойство
(5.3)
Пример 1. Проверим правильность формул
; 
;
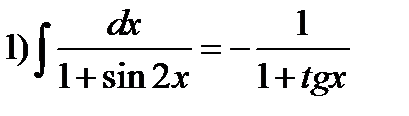Решение. Используем свойство (5.1)
Свойства (5.1),(5.3) показывают нам, что операции дифференцирования и неопределённого интегрирования являются взаимно обратными с точностью до произвольной постоянной.
Практически любой метод неопределённого интегрирования заключается в следующем. Используя свойства и правила интегрирования, мы преобразуем интеграл к известному табличному интегралу.
Существует три основных метода интегрирования 
Метод замены переменной интегрирования в неопределённом интеграле
Постановка задачи. Пусть задана функция . Требуется найти первообразную функцию 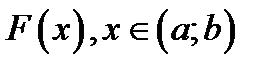такую, что .
Первое правило замены переменной. Прямая замена. Требуется найти 
.
Заменяем переменную интегрирования по правилу 
.
Имеем 
. Допустим, что замена 
такова,
что неопределённый интеграл 
известен и равен 
, то есть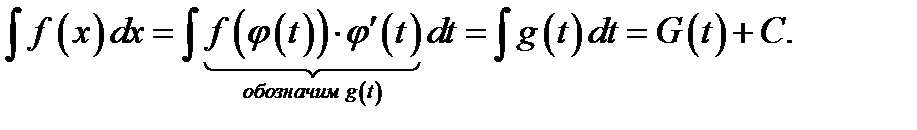 
Обращая равенство , получаем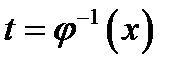 
и записываем ответ 
.
Пример 2. Найти первообразные функции 
Решение. Решаем 1). Чтобы подынтегральное выражение упростилось, положим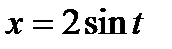 
.
Тогда
Таким образом
Чтобы получить ответ нужно вернуться от переменной 
к старой переменной 
Откуда 
Проверка полученного результата 
Или 
;
Решаем 2). Чтобы подынтегральное выражение упростилось, положим 
.
Тогда
Таким образом
Чтобы получить ответ нужно вернуться от переменной к старой переменной
Откуда 
Проверка полученного результата
Второе правило замены переменной.
Пусть требуется вычислить интеграл 
. Если можно разложить подынтегральную функцию 
на два множителя 
, то
Если известно, что 
то
Чтобы получить ответ нужно вернуться от переменной к старой переменной
.
Пример 3. Найти неопределённые интегралы
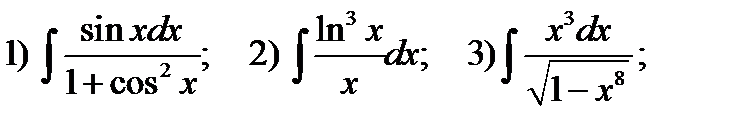
Решение. Решаем 1). Разлагаем подынтегральную функцию 
на два сомножителя 
. Тогда подынтегральное выражениебудет равно
. Производим замену переменной по правилу 
и в результате получаем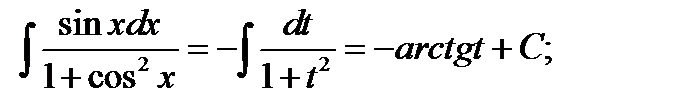 
возвращаясь к старой переменной, записываем ответ 
Проверка полученного результата: 
Решаем 2). Разлагаем подынтегральную функцию на два сомножителя 
. Тогда подынтегральное выражениебудет равно
. Производим замену переменной по правилу 
и в результате получаем 
;
Возвращаясь к старой переменной, записываем ответ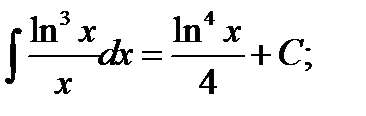 
Решаем 2). Разлагаем подынтегральную функцию на два сомножителя 
. Тогда подынтегральное выражениебудет равно
. Производим замену переменной по правилу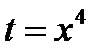 
и в результате получаем 
;
Возвращаясь к старой переменной, записываем ответ 
