Виды действий (манипуляций) над данными в реляционной модели представляют собой множество операций, получивших в совокупности название реляционной алгебры, и реляционной операции присваивания. Последняя производит присваивание значения некоторого производного выражения реляционной алгебры другому отношению.
Каждая операция реляционной алгебры использует одно или два отношения в качестве операндов и создает в результате некоторое новое отношение. Э. Коддом были определены восемь таких операций, объединенные в две группы по четыре операции в каждой.
Первая группа - традиционные теоретико-множественные операции.
В каждой из этих операций используется два операнда (отношения).
Для всех операций, кроме декартова произведения, эти два операнда должны быть совместимы по объединению, т.е. они должны быть одной степени, и их i -e атрибуты (
) должны быть связаны с одним и тем же доменом.
Операция объединение. Объединением двух отношений A и B называется множество всех кортежей t, принадлежащих либо A, либо B, либо им обоим. Символически эта операция показана на рис. 4.9а. Математически эта операция записывается так:
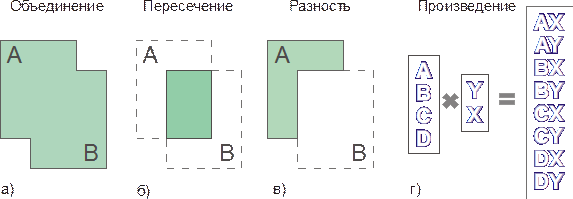
Рис.4.9 Диаграммы традиционных теоретико-множественных операций
;
где 
-символ объединения, 
- знак принадлежности к определенному отношению (множеству).
Операция пересечения. Пересечением двух отношений A и B называется множество всех кортежей t, каждый из которых принадлежит как A, так и B (рис. 4.9б):
,
где 
- символ пересечения.
Операция разность. Разностью между двумя отношениями A и B называется множество всех кортежей t, каждый из которых принадлежит A и не принадлежит B (рис. 4.9в):
,
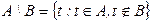где \ - символ разности,
- символ отсутствия принадлежности отношению (множеству).
Операция декартово произведение. Декартовым произведением двух отношений A и B называется множество всех кортежей t, таких, что t является конкатенацией некоторого кортежа а, принадлежащего A, и какого-либо кортежа b, принадлежащего B. (конкатенация - это соединение в цепочки). Для рисунка 4.9г декартово произведение:
.
Вторая группа - специальные реляционные операции. Диаграммы этих операций приведены на рис. 4.10.
Операция селекция. Пусть theta представляет собой любой достижимый оператор сравнения скаляров, например, 
и т.д. Theta - селекцией отношения А по атрибутам x и y называется множество всех кортежей t из А, таких, что истинен предикат „ t. x theta t. y. “ Атрибуты x и y должны быть определены на одном и том же домене, и для этого домена оператор theta должен иметь смысл. Вместо атрибута y может быть задана константа (например, выбрать из платежной ведомости записи о своих сотрудниках имеющих зарплату 500 руб.). Таким образом оператор theta - селекции позволит получать „горизонтальные“ подмножества заданного отношения, т.е. подмножество таких кортежей заданного отношения, для которых выполняются поставленное условие (рис. 4.10а).
Операция проекция. Операция проекция позволяет получить „вертикальное“ подмножество заданного отношения, т.е. такое подмножество,
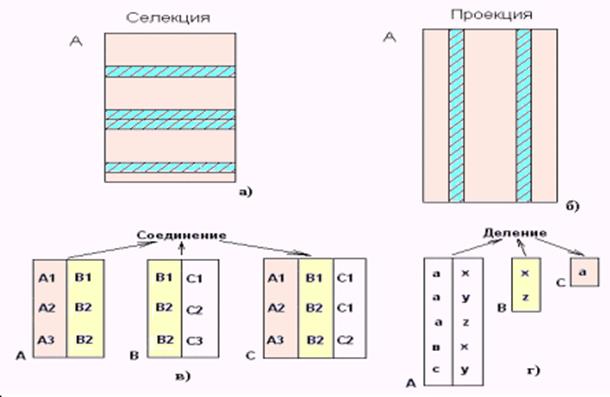
Рис.4.10 Диаграммы специальных реляционных операций
которое получается выбором специфицированных (определенных) атрибутов с последующим исключением, если это необходимо, избыточных дубликатов кортежей, состоящих из значений выбранных атрибутов (рис. 4.10б).
Операция соединение. Пусть theta имеет тот же смысл, что и в операции селекции. Тогда theta - соединением отношения А по атрибуту x с отношением В по атрибуту y называется множество всех кортежей t, таких, что t является конкатенацией какого-либо кортежа а, принадлежащего А, и какого-либо кортежа b, принадлежащего В, и предикат „ а. x theta b. y. “ принимает значение „истина“. При этом атрибуты А. x и В. y должны быть определены на одном и том же домене, а оператор theta должен иметь смысл для этого домена. Если оператор theta - равенство, то соединение называется экви - соединением.. Из этого определения следует, что результат экви-соединения должен включать два идентичных атрибута. Если один из этих атрибутов исключается, что можно осуществить с помощью проекции, результат называется естественным соединением. Под неуточненным термином „соединение“ понимают естественное соединение. Операция „соединение“ похожа на декартово произведение. Отличие состоит в том, что декартово произведение предполагает сцепление каждого кортежа из отношения А с каждым кортежем из В, а в операции соединения кортеж из отношения А сцепляется только с теми кортежами из В, для которых выполнено условие „a. x = b. y. “ Диаграмма операции приведена на рис. 4.10в.
Операция деление. В простейшей форме операция деления делит отношение степени два (делимое) на отношение степени один (делитель) и создает (продуцирует) результирующее отношение степени один (частное). Пусть делимое А имеет атрибуты x и y, а делитель В атрибут y (см. рис.4.10г). Атрибуты А. y и B. y должны быть определены на одном домене. Результатом деления А на В является отношение С с единственным атрибутом x, таким, что каждое значение x этого атрибута C. x появляется как значение А. x, а пара значений (x,y) входит в А для всех значений y, входящих в В. Другими словами, кортеж включается в результирующее отношение С только в том случае, если его декартово произведение с отношением В содержит отношение А.
Из восьми рассмотренных реляционных операций пять являются базовыми. Это - селекция, проекция, декартово произведение, объединение и разность. Остальные три операции могут быть определены через базовые. Например, естественное соединение может быть выражено как проекция селекции декартова произведения.
Назначение реляционной операции присваивания состоит в том, чтобы сохранить значение какого-либо алгебраического выражения, например, проекции в виде заданного отношения (таблицы).
Операции реляционной модели данных представляют возможность произвольно манипулировать отношениями, позволяя обновлять БД, а также выбирать подмножества хранимых данных и представлять их в нужном виде. Таким образом, особенностями, определившими преимущества реляционной модели, являются:
а) множество объектов реляционной модели БД однородно - структура БД определяется только в терминах отношений;
б) основная единица обработки в операциях реляционной модели не запись (как в сетевых и иерархических моделях), а множество записей - отношение.
