| № | Вопрос | Ответ | ||||||||||||||
| Гипергеометрическое распределение соответствует выборочному контролю качества: | Без возвращения | |||||||||||||||
| Вероятность того, что в выборке объемом n окажется х бракованных деталей, согласно гипергеометрическому закону запишется: | 
| |||||||||||||||
| Вероятность того, что в выборке объемом n окажется х бракованных деталей, согласно биномиальному закону запишется: | 
| |||||||||||||||
| Вероятность того, что в выборке объемом n окажется х или более бракованных деталей, согласно биномиальному закону запишется: | 
| |||||||||||||||
| Вероятность того, что в выборке объемом n окажется х бракованных деталей, согласно закону Пуассона запишется: | 
| |||||||||||||||
| В ящике лежит 6 деталей, две из них бракованные. Вероятность того, что из двух выбранных деталей одна является бракованной с использованием гипергеометрического закона равна: | 8/15 | |||||||||||||||
| Вероятность того, что в выборке объемом n окажется х или более бракованных деталей, согласно закону Пуассона запишется: | 
| |||||||||||||||
| В ящике лежит 10 деталей, две из них бракованные. Вероятность того, что из трех выбранных деталей не будет ни одной бракованной с использованием гипергеометрического закона равна: | 42/90 | |||||||||||||||
| В ящике лежат 1000 деталей. Десять из них бракованные. Вероятность того, что в выборке объемом 100 деталей нет ни одной бракованной детали, с использованием биномиального закона равна: | 0,366 | |||||||||||||||
| В ящике лежат 100 деталей. Девять из них бракованные. Вероятность того, что в выборке объемом 20 деталей есть три бракованные детали, с использованием биномиального закона равна: | 0,1673 | |||||||||||||||
| Статистический метод управления процессами предложил и разработал: | У. Шухарт | |||||||||||||||
| Контроль качества направлен на: | Отбраковку несоответствующей продукции. | |||||||||||||||
| Контрольные карты Шухарта направлены на: | Профилактику проблем и предотвращение брака. | |||||||||||||||
| Все виды продукции и услуг, а также все процессы, в которых они создаются и/или преобразуются, подвержены отклонениям от заданных значений, называемых вариациями. Причины этих вариаций согласно Шухарта делятся на: | Общие и специальные. | |||||||||||||||
| Общими причинами вариаций называют: | Причины, являющиеся неотъемлемой частью данного процесса и внутренне ему присущие. | |||||||||||||||
| Специальными причинами вариаций называют: | Причины, которые возникают из-за внешних по отношению к процессу воздействий на него и не являются его неотъемлемой частью. | |||||||||||||||
| Общие причины вариаций требуют: | Вмешательства в систему, требующего управленческих решений. | |||||||||||||||
| Специальные причины вариаций требуют: | Локального вмешательства в процесс, осуществляемого линейным персоналом. | |||||||||||||||
| Научное обоснование современных методов выборочного контроля и разработка первых таблиц связано с именами таких известных статистиков и специалистов в области менеджмента качества как: | Х. Додж. Х. Роминг. | |||||||||||||||
| В состав семи простых инструмента качества входят следующие три инструмента: | Гистограмма, контрольный листок, причинно-следственная диаграмма. | |||||||||||||||
| Классическое определение вероятности состоит в следующем: | Вероятностью случайного события А называют отношение числа благоприятных для данного события случаев к числу единственно возможных, равновозможных и несовместимых случаев. | |||||||||||||||
| Вероятность того, что при бросании игральной кости два раза подряд выпадет первый раз цифра 1, а второй - цифра 3 равна: | 1/36 | |||||||||||||||
| Вероятность того, что не произойдет ни одно из двух несовместных событий А и Б, если вероятность того, что произойдет событие А составляет 0,1, а событие Б - 0,2 равна: | 0,72 | |||||||||||||||
| Вероятность того, что при четырех бросаниях монеты все четыре раза выпадет орел, равна: | 1/16 | |||||||||||||||
| В ящике находится 100 гаек, среди которых одна бракованная. Вы вытаскиваете наугад две детали. Какое событие при этом является достоверным: | Вы вытащили две гайки. | |||||||||||||||
| В ящике находится 100 гаек, среди которых одна бракованная. Вы вытаскиваете наугад две детали. Какое событие при этом является случайным: | Обе гайки годные. Одна гайка годная, а вторая бракованная. | |||||||||||||||
| В ящике находится 100 гаек, среди которых одна бракованная. Вы вытаскиваете наугад две детали. Какое событие при этом является невозможным: | Обе гайки бракованные | |||||||||||||||
| Контролер контролирует диаметр партии цилиндрических деталей. Для контроля он использует проходной и непроходной калибры. Что является результатом контроля: | Случайное событие. | |||||||||||||||
| Законом статистической устойчивости называют: | Стремление относительной частоты события при увеличении числа испытаний к некоторому предельному значению. | |||||||||||||||
| Вероятность того, что произойдет одно из двух несовместных событий А и Б, если вероятность того, что произойдет событие А составляет 0,1, а событие Б - 0,2 равна: | 0,3 | |||||||||||||||
| В установке последовательно расположены три узла А, Б, и В, вероятность выхода из строя которых равна соответственно 0,1; 0,2 и 0,1. Вероятность выхода из строя всей установки равна: | 0,352 | |||||||||||||||
| В установке параллельно расположены три узла А, Б, и В, вероятность выхода из строя которых равна соответственно 0,1; 0,2 и 0,1. Вероятность выхода из строя всей установки равна: | 0,002 | |||||||||||||||
| Графическое представление распределения в виде гистограммы используют для следующих случайных величин: | непрерывных в виде интервального ряда | |||||||||||||||
Выберите правильное выражение для вероятности того, что случайная приведенная величина u находится в диапазоне  , если , если 
| 
| |||||||||||||||
Выберите правильное выражение для вероятности того, что случайная приведенная величина u находится в диапазоне  , если , если 
| 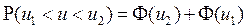
| |||||||||||||||
Процент случайных величин, лежащих в диапазоне  , найденный с помощью таблиц функции Лапласа, равен: , найденный с помощью таблиц функции Лапласа, равен:
| 99,73 | |||||||||||||||
Выберите правильное выражение для вероятности того, что случайная приведенная величина u находится в диапазоне  , если , если 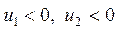 , , 
| 
| |||||||||||||||
Процент случайных величин, лежащих вне диапазона  , найденный с помощью таблиц функции Лапласа, равен: , найденный с помощью таблиц функции Лапласа, равен:
| 0,27 | |||||||||||||||
| Сроки службы ламп накаливания распределены нормально, причем средний срок службы равен 2000 часов, а стандартное отклонение 200 часов. Определить процентное содержание ламп, которые проработают менее 1500 часов: | 0,0062 | |||||||||||||||
| Сроки службы ламп накаливания распределены нормально, причем средний срок службы равен 2500 часов, а стандартное отклонение 500 часов. Определить процентное содержание ламп, которые проработают более 3000 часов: | 0,1587 | |||||||||||||||
Процент случайных величин, лежащих в диапазоне 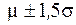 , найденный с помощью таблиц функции Лапласа, равен: , найденный с помощью таблиц функции Лапласа, равен:
| 86,64 | |||||||||||||||
Процент случайных величин, лежащих в диапазоне  , найденный с помощью таблиц функции Лапласа, равен: , найденный с помощью таблиц функции Лапласа, равен:
| 95,44 | |||||||||||||||
| Что означает факт наличия особых структуры точек, обнаруженных на контрольной карте Шухарта: | Их наличие на контрольной карте также мало вероятно, как и выход точки за контрольные границы Их наличие на контрольной карте, вероятно, означает появление особой причины, влияющей на процесс Их наличие на контрольной карте служит сигналом о возможном выходе процесса из состояния статистической управляемости | |||||||||||||||
| Найдите вероятность того что девять точек подряд на контрольной карте Шухарта находятся по одну сторону от центральной линии: | 0,0019 | |||||||||||||||
| Найдите вероятность того что пятнадцать последовательных точек на контрольной карте Шухарта находятся в зоне С выше или ниже центральной линии: | 0,0032 | |||||||||||||||
| Назначение системы управления процессом при помощи контрольных карт Шухарта состоит в получении статистического сигнала о наличии особых (неслучайных) причин вариаций. Систематическое устранение особых причин избыточной изменчивости приводит процесс в состояние статистической управляемости. Если процесс находится в статистически управляемом состоянии то: | Качество продукции предсказуемо, и процесс пригоден для удовлетворения требований, установленных в нормативных документах | |||||||||||||||
| Возможности процесса определяются: | Полной изменчивостью (разбросом процесса), обусловленной обычными причинами Минимальной изменчивостью, которая остается после устранения всех неслучайных причин | |||||||||||||||
| Определение возможностей процесса поставщика начинается: | После того как задача управления процесса по  - и R -картам решена - и R -картам решена
| |||||||||||||||
| Текущие контрольные карты должны демонстрировать сохранение процесса в статистически управляемом состоянии: | По крайне мере для 25 подгрупп | |||||||||||||||
| Индекс возможностей процесса равен: | Верхнее предельное отклонение минус нижнее предельное отклонение, деленное на поле разброса процесса Поле допуска, деленное на шесть сигм | |||||||||||||||
| np карты - это: | Контрольные карты для числа несоответствующих единиц продукции | |||||||||||||||
| Контрольные карты кумулятивных сумм: | Более чувствительны к выявлению изменений в уровне исследуемого параметра, чем традиционные карты | |||||||||||||||
| Графическое представление распределения в виде многоугольника распределения используют для следующих случайных величин | Дискретных | |||||||||||||||
| Распределение непрерывной случайной величины достаточно сложно представить в виде ряда распределения вследствие следующих причин | И первая и вторая причины могут иметь место | |||||||||||||||
1. Результаты эксперимента представлены в следующей таблице:
Представление данных в виде такой таблицы называют: | Рядом распределения | |||||||||||||||
| Функция распределения случайной величины F (x) это: | Вероятность того, что случайная величина Х меньше х | |||||||||||||||
| В качестве признаков качества металлопродукции на предприятии используют: A Диаметр детали. B Массу детали. C Наличие или отсутствие трещин на поверхности детали. D Наличие или отсутствие внутренних пор. E Результат контроля диаметра детали проходным и непроходным калибрами. F Твердость поверхности детали, измеряемая твердомером. Какие из этих признаков являются альтернативными: | C, D, Е | |||||||||||||||
| В качестве признаков качества металлопродукции на предприятии используют: A Диаметр детали. B Массу детали. C Наличие или отсутствие трещин на поверхности детали. D Наличие или отсутствие внутренних пор. E Результат контроля диаметра детали проходным и непроходным калибрами. F Твердость поверхности детали, измеряемая твердомером. Какие из этих признаков относятся к количественным признакам: | A, B, F | |||||||||||||||
| Вес булки хлеба является | Непрерывной случайной величиной | |||||||||||||||
| Распределение случайных величин это | совокупность ее значений, расположенная в возрастающем порядке с указанием ее вероятности (или частости) | |||||||||||||||
| Для представления (описания) распределения случайных величин используют следующие методы | Графический, табличный; функцией распределения, плотностью распределения | |||||||||||||||
| Функция распределения случайной величины F (x) запишется следующей формулой | 
| |||||||||||||||
| Функция распределения случайной величины F (x) есть: | Неубывающая функция своего аргумента | |||||||||||||||
| Вероятность попадания случайной величины Х на отрезок от х 1 до х 2 выраженная через функцию распределения равна: | 
| |||||||||||||||
| Плотность распределения случайной величины это: | Производная функции распределения случайной величины | |||||||||||||||
| Вероятность попадания случайной величины Х на отрезок от х 1 до х 2 выраженная через плотность распределения равна: | 
| |||||||||||||||
| Значение интеграла плотности распределения случайной величины в пределах от минус бесконечности до плюс бесконечности равно: | Единице | |||||||||||||||
| Плотность распределения есть: | Неотрицательная величина при всех значениях аргумента | |||||||||||||||
| Какой из предложенных ответов содержит верный и наиболее полный ряд статистик, характеризующих положение случайных величин распределения на числовой оси: | Математическое ожидание, медиана, среднее арифметическое | |||||||||||||||
| Какой из предложенных ответов содержит верный и наиболее полный ряд статистик, характеризующих рассеивание случайных величин распределения: | Дисперсия, стандартное отклонение, размах | |||||||||||||||
| Какой из ответов содержит верную формулу определения математического ожидания распределения дискретных случайных величин? | 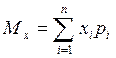
| |||||||||||||||
| Какой из ответов содержит верную формулу определения математического ожидания распределения непрерывных случайных величин | 
| |||||||||||||||
| Целью выборочного приемочного контроля качества является: | Обеспечение поставки потребителю продукции заданного уровня качества, независимо от того, насколько управляем технологический процесс | |||||||||||||||
| Приемочный контроль находит применение: | При осуществлении всех перечисленных видов контроля качества | |||||||||||||||
| Сплошной контроль рекомендуется: | В тех случаях, когда он технически возможен и экономически целесообразен | |||||||||||||||
| Выборочный контроль обычно проводится в тех случаях, когда: | Во всех перечисленных выше случаях | |||||||||||||||
| При выборочном контроле решение о качестве предъявляемой на контроль партии продукции принимается в случае: | Во всех перечисленных выше случаях | |||||||||||||||
| Выборочный контроль по альтернативному признаку по сравнению с выборочным контролем по количественному признаку: | В общем случае более прост в организации и предъявляет меньшие требования к оборудованию и квалификации персонала | |||||||||||||||
| Применение двухступенчатых планов позволяет: | Снизить по сравнению с одноступенчатым планом среднее число проконтролированных изделий При том же среднем объеме выборки получить большую достоверность соответствия принимаемых решений с истинным положением дела | |||||||||||||||
| Какой из ответов содержит верную формулу определения среднего арифметического распределения случайных величин, выраженного в виде интервального ряда: | 
| |||||||||||||||
| Какой из ответов содержит верную формулу определения среднего арифметического распределения случайных величин, выраженного в виде упорядоченного ряда, если значения величин не повторяются: | 

| |||||||||||||||
| Какой из ответов содержит верную формулу для определения дисперсии случайных величин, полученных на выборке объемом 25, если значения измеренных величин не повторялись: | 
| |||||||||||||||
| Какой из ответов содержит верную формулу для определения дисперсии случайных величин, полученных на выборке объемом 50, если значения измеренных величин не повторялись: | 
| |||||||||||||||
| Какой из ответов содержит верную формулу для определения дисперсии случайных величин, полученных на выборке объемом 50, если значения измеренных величин повторялись: | 
| |||||||||||||||
| Какой из ответов содержит верную формулу для определения дисперсии случайных величин, полученных на выборке объемом 20, если значения измеренных величин повторялись: | 
| |||||||||||||||
| Медианой случайной величины (Ме) называют: | Такое её значение, для которого функция распределения равна ½ | |||||||||||||||
| Стандартное отклонение - это: | Корень квадратный из дисперсии | |||||||||||||||
| Размахом распределения случайной величины называют | Разность между наибольшим и наименьшим измеренными значениями случайной величины | |||||||||||||||
| В электросталеплавильном цехе металлургического комбината в среднем две плавки из ста выходят за пределы марочного химического состава. Для выполнения очередного заказа требуется металл пятидесяти плавок. Используя закон Пуассона, определите вероятность того, что весь выплавленный для этого заказа металл будет иметь марочный состав: | 0,3679 0,6065 | |||||||||||||||
| Количество интервалов представления распределения случайных величин в виде интервального ряда должно быть: | Не менее шести и не более двадцати | |||||||||||||||
| В партии деталей имеется 3% процента брака. Из партии взята выборка объемом 40 деталей. Найти вероятность того, что в этой выборке имеется 3 бракованные детали: | 0,0867 | |||||||||||||||
| При организации контроля качества целесообразно использовать сплошной контроль в следующих случаях: | Если использование дефектных изделий представляет потенциальную опасность больших убытков или угрозы для жизни потребителя | |||||||||||||||
| Введение сплошного контроля качества нецелесообразно вследствие действия следующих факторов | Всех перечисленных | |||||||||||||||
| Случайная выборка отличается следующими особенностями: | Если все детали генеральной совокупности имеют равную возможность попасть в выборку | |||||||||||||||
| В процессе жизненного цикла продукции возникают следующие задачи. A Разбраковка деталей, готовой продукции. B Оценка статистической управляемости процесса. C Установление закона распределения изучаемой случайной величины и его параметров. D Статистическая проверка гипотез, выдвигаемых при производстве. Какие из них относятся к задачам выборочного контроля? | A, B, C, D | |||||||||||||||
Средняя арифметическая  распределения выборочных средних распределения выборочных средних 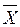
| Совпадает с математическим ожиданием генеральной совокупности | |||||||||||||||
| Дисперсия распределения выборочных средних значений равна: |  где
где  - дисперсия генеральной совокупности - дисперсия генеральной совокупности
| |||||||||||||||
| Если генеральная совокупность случайных величин имеет логарифмический закон распределения, то распределение выборочных средних для двухсот взятых выборок приближается к: | Нормальному | |||||||||||||||
| В партии деталей имеется 3% процента брака. Из партии взята выборка объемом 40 деталей. Найти вероятность того, что в этой выборке имеется не менее трех бракованных деталей: | 0,3773 | |||||||||||||||
| Поставщик для оценки годности партий готовой продукции организует выборочный контроль без возвращения. Наиболее правильную оценку вероятности наличия в выборке бракованных изделий при теоретических расчетах дает закон: | Гипергеометрический | |||||||||||||||
| Числовые характеристики распределения случайных величин, подчиняющихся гипергеометрическому закону распределения равны: | 

| |||||||||||||||
| Числовые характеристики распределения случайных величин, подчиняющихся биномиальному закону распределения равны: | 

| |||||||||||||||
| Числовые характеристики распределения случайных величин, подчиняющихся закону распределения Пуассона равны: | 

| |||||||||||||||
| Распределение, подчиняющееся биномиальному закону, является: | Симметричным при р =0,5 и ассиметричным при остальных р | |||||||||||||||
| Если случайная величина х представляет собой сумму очень большого числа взаимно независимых случайных величин х 1, х 2, х 3, … х n, влияние каждой из которых на всю сумму ничтожно мало, то независимо от того, каким законам распределения подчиняются слагаемые х 1, х 2, х 3, … х n сама величина х будет иметь распределение вероятности близкое к: | Нормальному | |||||||||||||||
| Плотность распределения случайной величины х непрерывного типа, подчиняющейся нормальному закону распределения, имеет следующий вид: | 
| |||||||||||||||
| Функция распределения случайной величины х непрерывного типа, подчиняющейся нормальному закону распределения, имеет следующий вид: | 
| |||||||||||||||
| Функция Лапласа распределения случайной нормированной величины u непрерывного типа, подчиняющейся нормальному закону распределения, запишется следующим образом: | 
| |||||||||||||||
| Графически плотность вероятности для нормального распределения выражается в виде: | Симметричной кривой холмообразного вида с максимумом для
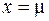
| |||||||||||||||
С уменьшением величины стандартного отклонения  кривая плотности распределения: кривая плотности распределения:
| Становится более высокой, а ее ветви сближаются | |||||||||||||||
| С уменьшением величины математического ожидания распределения случайной величины кривая плотности распределения: | Сдвигается в сторону меньшего значения параметра при неизменной форме | |||||||||||||||
| Величина интеграла вероятности (функции Лапласа) численно равна: | Площади под нормированной нормальной кривой распределения от 0 до u | |||||||||||||||
Выборочная нормированная характеристика  удовлетворяет нормированному нормальному распределению со следующими параметрами: удовлетворяет нормированному нормальному распределению со следующими параметрами:
| Математическое ожидание равно нулю, дисперсия равна единице | |||||||||||||||
Выборочная характеристика 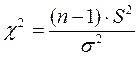 имеет плотность распределения имеет плотность распределения  : :
| Ассиметричную, но при n →∞ приближающуюся к плотности нормального распределения | |||||||||||||||
Выборочная характеристика  имеет плотность распределения имеет плотность распределения  (плотность распределения «Стьюдента»): (плотность распределения «Стьюдента»):
| Симметричную относительно нуля | |||||||||||||||
В токарном цехе изготавливают цилиндрические детали. Из продукции одного станка случайным образом отбирают 20 деталей и штангельциркулем измеряют их диаметр. Значение среднего арифметического выборки равно  мм. Величина дисперсии диаметров для станка составила по предварительным исследованиям мм. Величина дисперсии диаметров для станка составила по предварительным исследованиям  мм2. Можно ли на основании этих результатов сделать вывод о том, что станок постоянно обеспечивает заданный номинальный размер 12,0 мм, на который он был настроен в начале смены. Для решения поставленного вопроса необходимо: мм2. Можно ли на основании этих результатов сделать вывод о том, что станок постоянно обеспечивает заданный номинальный размер 12,0 мм, на который он был настроен в начале смены. Для решения поставленного вопроса необходимо:
| Проверить гипотезу о среднем значении нормально распределённой генеральной совокупности при известной дисперсии | |||||||||||||||
| Для проверки гипотезы о среднем значении нормально распределенной генеральной совокупности при известной ее дисперсии используется критерий: | 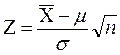
| |||||||||||||||
| Для проверки гипотезы о среднем значении нормально распределенной генеральной совокупности при неизвестной ее дисперсии используется критерий: | 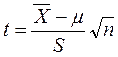
| |||||||||||||||
| Для проверки гипотезы о дисперсии нормально распределенной генеральной совокупности используется критерий: | 
| |||||||||||||||
| Для проверки гипотезы о значениях двух дисперсий нормально распределенных генеральных совокупностей используется критерий: | 
| |||||||||||||||
| Для проверки гипотезы о законе распределения генеральной совокупности используется критерий согласия: | Оба критерия | |||||||||||||||
Выражение  используют для: используют для:
| Нахождения критического отклонения 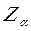 , при котором гипотеза о средней величине генеральной совокупности при известной дисперсии отвергается , при котором гипотеза о средней величине генеральной совокупности при известной дисперсии отвергается
| |||||||||||||||
Выражение  используют для: используют для:
| Нахождения критического отклонения  , при котором гипотеза о средней величине генеральной совокупности при неизвестной дисперсии отвергается , при котором гипотеза о средней величине генеральной совокупности при неизвестной дисперсии отвергается
| |||||||||||||||
Объем выборки при проведении контроля составил 11 деталей. При уровне значимости 0,05 найти величину 
| 2,23 | |||||||||||||||
Объем выборки при проведении контроля составил 250 деталей. При уровне значимости 0,05 найти величину  : :
| 1,96 | |||||||||||||||
| Вал имеет номинальный диаметр 90,018 мм. Измерялась выборка объемом 10 валов. Результаты обработки полученных данных следующие: | Гипотеза принимается | |||||||||||||||
Вал имеет номинальный диаметр 90,018 мм. Измерялась выборка объемом 10 валов. Результаты обработки полученных данных следующие:
 = 90,016 мм, = 90,016 мм,  =30 μкм2, =30 μкм2,  = 5,48 μкм.
Проверьте гипотезу: = 5,48 μкм.
Проверьте гипотезу:  = 90,018. = 90,018.
| Для проверки гипотезы не хватает данных | |||||||||||||||
Из партии деталей взята выборка объемом n = 20 и произведены измерения их диаметров, по которым рассчитаны статистические характеристики: 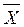 = 20 мм, = 20 мм, 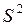 = 841 µкм2, = 841 µкм2,  = 29 µкм. Можно ли по результатам выборки заключить, что она взята из генеральной совокупности с = 29 µкм. Можно ли по результатам выборки заключить, что она взята из генеральной совокупности с  = 20 µкм. Для этого проверьте гипотезу = 20 µкм. Для этого проверьте гипотезу  при α = 0,01. при α = 0,01.
| Гипотеза отвергается | |||||||||||||||
Из партии деталей взята выборка объемом n = 30 и произведены измерения их длин, по которым рассчитаны статистические характеристики: 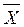 = 120 мм, = 120 мм, 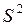 = 9 мм2, = 9 мм2,  = 3 мм. Можно ли по результатам выборки заключить, что она взята из генеральной совокупности с = 3 мм. Можно ли по результатам выборки заключить, что она взята из генеральной совокупности с  = 3,5 мм. Для этого проверьте гипотезу = 3,5 мм. Для этого проверьте гипотезу  при α = 0,01. при α = 0,01.
| Для проверки гипотезы не хватает данных | |||||||||||||||
При проверке гипотезы  получены следующие данные: получены следующие данные:  . Это говорит о том, что: . Это говорит о том, что:
| При объеме выборки n = 20 и уровне значимости 0,01 гипотеза отвергается | |||||||||||||||
При проверке гипотезы  получены следующие данные: получены следующие данные:  . Это говорит о том, что: . Это говорит о том, что:
| При объеме выборки n = 10 и уровне значимости 0,05 гипотеза принимается | |||||||||||||||
| Назначенный вид ослабленного контроля по альтернативному признаку согласно ГОСТ Р 50779.71-99 продолжают до тех пор, пока не возникает необходимость выполнить переключение на нормальный контроль. Правило переключения выглядит следующим образом: | Партия не принята приемщиком Изменились условия производства | |||||||||||||||
При проверке гипотезы  получены следующие данные: получены следующие данные:  . Это говорит о том, что: . Это говорит о том, что:
| Объем первой выборки n = 15, а второй n = 22. Дисперсия измеренных параметров первой выборки больше, чем второй. Гипотеза принимается | |||||||||||||||
| Применение критерия Пирсона при проверке гипотезы нормальности распределения генеральной совокупности является обоснованным, если: | Ни одна из разрядных частей (интервалов разбиения исследуемой области) не будет содержать менее пяти зафиксированных значений | |||||||||||||||
В выражении для критерия Пирсона  параметр параметр 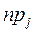 представляет собой: представляет собой:
| Теоретическую частоту j-того интервала значений х Теоретическое количество попаданий измеренного параметра в j-тый интервал значений х | |||||||||||||||
В выражении для критерия Пирсона  параметр параметр  представляет собой: представляет собой:
| Фактическое количество попаданий измеренного параметра в j-тый интервал значений х Фактическую частоту попаданий измеренного параметра в j-тый интервал значений х | |||||||||||||||
| Диаграмма рассеивания показывает: | Характер статистической зависимости между парами измеряемых признаков качества | |||||||||||||||
| Какая информация, из перечисленной ниже, может быть получена при анализе диаграммы рассеивания: A Наличие положительной корреляции между измеренными парами признаков качества. B Наличие отрицательной корреляции между измеренными парами признаков качества. C Отсутствие корреляции между измеренными парами признаков качества. D Наличие нелинейной корреляции между измеренными парами признаков качества. | А, B, C, D | |||||||||||||||
| Коэффициент корреляции дает информацию о: | Силе и направлении линейной связи между значениями  и и 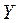
| |||||||||||||||
| Коэффициентом корреляции называют соотношение: | 
| |||||||||||||||
| Коэффициент корреляции может принимать следующие значения: | От -1 до +1 | |||||||||||||||
Значение коэффициента корреляции  говорит о: говорит о:
| Слабой связи между измеренными парами параметров качества | |||||||||||||||
| Какой метод положен в основу вывода формулы линейной регрессии: | Наименьших квадратов | |||||||||||||||
| Уравнение линейной регрессии изменения параметра Y по параметру X записывается следующим образом: | 
| |||||||||||||||
| Линия регрессии - это: | Линия, которая лежит возможно ближе к «множеству точек» на диаграмме рассеивания | |||||||||||||||
Выражение 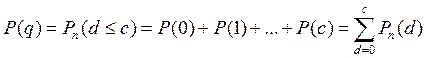 используют для: используют для:
| Построения оперативной характеристики одноступенчатого плана контроля по альтернативному признаку Построения зависимости вероятности приемки контролируемой партии продукции от величины параметра, характеризующего качество этой партии продукции | |||||||||||||||
| При построении оперативных характеристик одноступенчатого плана контроля используется следующее выражение: | Все выражения | |||||||||||||||
| При построении оперативных характеристик одноступенчатого плана контроля обычно используют следующее выражение: | Первое и второе | |||||||||||||||
| Чему равна вероятность браковки партии на основании результатов контроля второй выборки при реализации двухступенчатого плана контроля: | 
| |||||||||||||||
| Чему равна вероятность приемки партии на основании результатов контроля второй выборки при реализации двухступенчатого плана контроля: | 
| |||||||||||||||
| Вероятность того, что партия при заданном уровне несоответствий q будет принята после контроля первой или второй выборки, определяется следующим соотношением: | 
| |||||||||||||||
| Пусть вероятность приемки партии продукции при приемочном числе с = 4 и объеме выборки n = 50, для одноступенчатого плана контроля по альтернативному признаку рассчитана. Как изменится вероятность приемки при неизменном объеме выборки и увеличении приемочного числа до с = 5: | Увеличится | |||||||||||||||
| Пусть вероятность приемки партии продукции при приемочном числе с = 4 и объеме выборки n = 50, для одноступенчатого плана контроля по альтернативному признаку рассчитана. Как изменится вероятность приемки при неизменном объеме партии и уменьшении приемочного числа до с = 3: | Уменьшится | |||||||||||||||
| Назначенный вид нормального контроля по альтернативному признаку согласно ГОСТ Р 50779.71-99 продолжают до тех пор, пока не возникает необходимость выполнить переключение на усиленный контроль. Правило переключения выглядит следующим образом: | Не менее двух из пяти последовательных партий отклонены | |||||||||||||||
| Назначенный вид усиленного контроля по альтернативному признаку согласно ГОСТ Р 50779.71-99 продолжают до тех пор, пока не возникает необходимость выполнить переключение на нормальный контроль. Правило переключения выглядит следующим образом: | Пять последовательных партий приняты приемщиком | |||||||||||||||
| Пусть вероятность приемки партии продукции при приемочном числе с = 4 и объеме выборки n = 50, для одноступенчатого плана контроля по альтернативному признаку рассчитана. Как изменится вероятность приемки при неизменном приемочном числе и увеличении объема выборки до n = 100: | Увеличится | |||||||||||||||
| План выборочного контроля - это: | Система правил и критериев организации, проведения контроля и принятия решения по его результатам о приемке всей партии | |||||||||||||||
| Оперативная характеристика - это: | Зависимость вероятности приемки контролируемой партии продукции от величины параметра, характеризующего качество этой партии продукции | |||||||||||||||
| Согласно ГОСТ Р 50779.71-99 «Процедуры выборочного контроля по альтернативному признаку» выборочные планы распространяются на контроль следующих объектов: | Всех перечисленных объектов | |||||||||||||||
| Основой для выбора планов и схем контроля при выборочном контроле последовательных партий на основе приемлемого уровня качества (AQL) по ГОСТ Р 50779.71-99 являются: | AQL и код объема выборки | |||||||||||||||
| Уровень AQL для выбора плана контроля по альтернативному признаку согласно ГОСТ Р 50779.71-99: | Оговаривается в контракте | |||||||||||||||
| При выборе кода объема выборки по ГОСТ Р 50779.71-99, если нет других предписаний, пользуются: | Общим уровнем 2 | |||||||||||||||
| На начальном этапе контроля по альтернативному признаку согласно ГОСТ Р 50779.71-99 устанавливают следующий вид контроля: | Нормальный | |||||||||||||||
| Оперативная характеристика может быть выражена | Всеми перечисленными способами | |||||||||||||||
| Приемлемый уровень качества - это: | Максимальный уровень несоответствий в партии продукции, который для целей приемки продукции рассматривается как удовлетворительный | |||||||||||||||
| Риск поставщика - это: | Риск забраковать партию продукции, соответствующую установленным требованиям к ее качеству Вероятность браковки партии продукции, соответствующую установленным требованиям к ее качеству | |||||||||||||||
| Риск потребителя - это: | Риск принять партию продукции, не соответствующую установленным требованиям к ее качеству Вероятность принятия партии продукции, не соответствующую установленным требованиям к ее качеству | |||||||||||||||
| Предельное допустимое качество (Limiting Quality) - это: | Уровень несоответствий, соответствующий риску потребителя | |||||||||||||||
| 112 План контроля по альтернативному признаку включает в себя следующее: порядок отборки изделий для контроля, объем выборки, ………………………. В этом перечне пропущен следующий параметр плана: | Допустимое количество бракованных изделий в выборке Приемочное число с | |||||||||||||||
| План контроля разрабатывается на основе: | Статистических методов | |||||||||||||||
| Какой из перечисленных планов контроля по альтернативному признаку не используется на практике? | Планы типа независимых выборок | |||||||||||||||
Если число обнаруженных дефектов в выборке d меньше или равно приемочному числу с ( ), то: ), то:
| Партия принимается при одноступенчатом плане контроля | |||||||||||||||
| Если число обнаруженных дефектов в выборке d больше приемочного числа с (d > с), то: | Партия не принимается при одноступенчатом плане контроля | |||||||||||||||
| Средний объем выборки для многоступенчатого плана контроля по ГОСТ Р 50779.71-99 по сравнению со средним объемом контроля для одноступенчатого плана: | Меньше | |||||||||||||||
| При выборочном контроле по количественному признаку качества полагают, что контролируемый параметр имеет точно или приближенно: | Нормальное распределение | |||||||||||||||
| В качестве аргумента оперативной характеристики плана выборочного контроля по количественному признаку используют: | Уровень несоответствий в контролируемой партии продукции q Среднее значение контролируемого параметра . | |||||||||||||||
| Квантиль уровня это: | Значение случайной величины, для которой функция распределения принимает значение | |||||||||||||||
| Влияние какой из ниженазванных причин не может быть обнаружено при помощи контрольных карт Шухарта: | Значительный разброс параметра качества, свойственный процессу | |||||||||||||||
| Цель контрольных карт: | Обнаружить наличие неестественных изменений в процессе | |||||||||||||||
| Карта Шухарта - это: | График значений, определяемых характеристик подгрупп (выборок) в зависимости от их номеров | |||||||||||||||
| Центральная линия карты Шухарта соответствует: | Эталонному значению измеряемой характеристики | |||||||||||||||
Контрольные границы карт Шухарта находятся на расстоянии  от центральной линии, где от центральной линии, где  : :
| Стандартное отклонение распределения выборочного параметра | |||||||||||||||
| Если значение характеристики на контрольной карте Шухарта оказалась за пределами контрольных границ, это означает, что: | Процесс вышел из состояния статистической управляемости с вероятностью 99,7% | |||||||||||||||
| Г87 | Любое выборочное значение, попадающее за границы  контрольных карт Шухарта, служит: контрольных карт Шухарта, служит:
| Предостережением о грозящей ситуации выхода процесса из состояния статистической управляемости | ||||||||||||||
| Система карт Шухарта учитывает: | Только ошибки первого рода | |||||||||||||||
| Для контрольных карт, использующих количественные данные, предполагается: | Нормальное распределение для вариаций внутри выборок | |||||||||||||||
Предположим, что из предыдущих исследований, либо из каких-то соображений известны стандартные значения генеральной совокупности численного параметра качества:  математическое ожидание и математическое ожидание и  стандартное отклонение. В этом случае верхняя контрольная граница откладывается от средней линии контрольной стандартное отклонение. В этом случае верхняя контрольная граница откладывается от средней линии контрольной  карты Шухарта на расстоянии: карты Шухарта на расстоянии:
| 
| |||||||||||||||
При управлении процессом при помощи контрольных карт  , ,  первой строится карта: первой строится карта:
| 
| |||||||||||||||
Если при построении контрольной  карты обнаружены точки вне границ, особые структуры или тренды, то: карты обнаружены точки вне границ, особые структуры или тренды, то:
| Выполняют все мероприятия по пунктам 1 и 2 | |||||||||||||||
Нижняя контрольная граница откладывается от средней линии контрольной  карты Шухарта для количественных данных на расстоянии: карты Шухарта для количественных данных на расстоянии:
| 
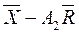
|





 5
5

