Задачи данного раздела составлены в соответствии с программой третьего семестра курса «Математика». Решения задач должны содержать все необходимые расчеты и пояснения. С учетом этого требования следует приводить, по возможности, краткие и четкие решения. При решении задач этого раздела следует использовать методы, описанные в учебно-методических пособиях «Типовые задачи базового уровня по математике с решениями» (части 3 и 4) [3]. В дальнейшем мы будем называть это пособие «Типовые задачи» и давать ссылки на его определенные разделы.
Задачи 1 – 8 составлены в соответствии с частью 3 данного учебно-методического пособия (раздел 2 «Введение в теорию вероятностей»). Задачи 1,2,3 соответствуют разделам 2.1 (Элементы комбинаторики) и 2.2 (Классическое определение вероятности) пособия «Типовые задачи», часть 3. Во всех этих задачах искомые вероятности определяются по классической формуле (раздел 2.2):
,
где 
- общее число элементарных исходов опыта, 
- число благоприятных элементарных исходов опыта. При вычислении числителя и знаменателя могут использоваться формулы комбинаторики (раздел 2.1).
Покажем в качестве примера возможный вариант оформления решения задачи 2. Пусть, например, номер варианта курсовой работы 
. Тогда один из возможных вариантов оформления решения может выглядеть следующим образом.
Задача 2. На один ряд, состоящий из 39 мест, случайно садятся 39 учеников. Найти вероятность того, что 3 определенных ученика окажутся рядом.
Решение. Случайный эксперимент – рассаживание 39 учеников в один ряд. Элементарный исход – перестановка из 39 элементов. Общее число таких перестановок 
. Благоприятными исходами являются те, в которых 3 конкретных ученика (например, те, которые имеют номера 1,2 и 3) окажутся рядом. Число таких исходов можно определить так. Тройка учеников, сидящих рядом, имеет 37 вариантов своего размещения среди 39 учеников, поскольку «самый левый» из этой тройки может сидеть на местах с 1-ого по 37-ое. Внутри этой тройки число вариантов размещения учеников равно 
. Остальные 36 учеников могут размещаться на оставшихся 36 местах числом способов, равным 
. Тогда число благоприятных элементарных исходов равно 
. Искомую вероятность определим по классической формуле:
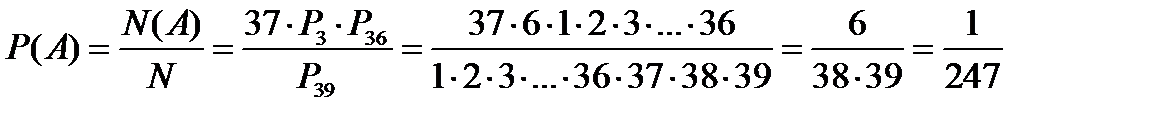
Ответ: 
.
Следует отметить, что приведенный вариант оформления решения является лишь одним из возможных. Способ изложения решения, так же, как и используемые обозначения, могут быть различными – такими, к каким студенты привыкли при проведении практических занятий.
Задачи 4 и 5 соответствует разделам 2.5 (Формула полной вероятности) и 2.6 (формула Бейеса) пособия «Типовые задачи», часть 3, соответственно. При их решении можно использовать логику примеров 2.5.1 и 2.6.1 соответственно.
Задачи 6 и 7 соответствует разделу 3.1 (Дискретные случайные величины), а задача 8 – разделу 3.2 (Непрерывные случайные величины) пособия «Типовые задачи», часть 3. При их решении следует использовать логику различных примеров из указанных разделов.
Задачи 9 – 16 составлены в соответствии с разделом «Законы распределения случайных величин»: №9 – биномиальное распределение; №10 – геометрическое распределение; №11 – распределение Пуассона в простейшем потоке; №12 – распределение Пуассона как закон «редких явлений»; №13 – равномерное распределение; №14 – показательное распределение; №15 – нормальное распределение (характеристики); №16 – нормальное распределение (правило «трех сигм»). Для решения задач данного раздела следует использовать материал разделов 2.7 (формула Бернулли), 3.3 (нормальный закон распределения) и 3.4 (показательный закон распределения) учебно-методического пособия «Типовые задачи». Формула Бернулли используется при определении характеристик биномиального распределения (задача №9). Также следует использовать материал соответствующих разделов учебника «Теория вероятностей и математическая статистика» (автор В.Н. Калинина).
План решения задач 9-16 может быть следующим: вводится случайная величина; определяется ее закон распределения; по исходным данным определяются параметры этого закона; зная закон распределения, определяются все требуемые характеристики рассматриваемой случайной величины.
В качестве примера рассмотрим решение задачи 11. Пусть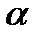 
= 35. Тогда один из возможных вариантов оформления решения может выглядеть следующим образом.
Задача 11. К киоску в среднем за 35 минут приходит 1 покупатель. Считая поток покупателей простейшим, найти вероятность того, что за 2 минуты к киоску подойдет: а) менее 2 покупателей; б) хотя бы 1 покупатель. Найти м.о. и с.к.о. числа покупателей за 1 минуту.
Решение. Рассмотрим случайную величину X – количество покупателей, подходящих к киоску за 2 минуты. Поскольку поток покупателей является простейшим, то случайная величина X имеет распределение Пуассона. Найдем его параметр. Интенсивность потока: 
. Параметр распределения Пуассона: 
. Теперь, используя формулу Пуассона, найдем искомые вероятности: 
; 
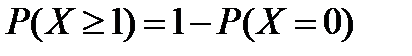. По формуле Пуассона: 
.
Тогда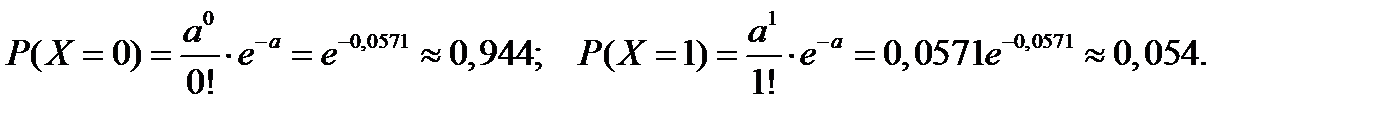 
Теперь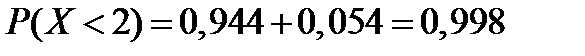 
; 
.
Используем формулы для числовых характеристик распределения Пуассона:
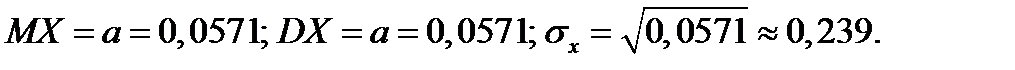
Ответ: а) 0,998; б) 0,056; 
Задачи 17 и 18 составлены в соответствии с частью 4 учебно-методического пособия «Типовые задачи» (раздел 4 «Математическая статистика»). Для решения задачи 15 следует изучить примеры 4.1.1, 4.2.1 и 4.4.1. Для решения задачи 16 следует изучить примеры 4.1.3, 4.3.1 и 4.3.2.
Еще раз отметим, что при оформлении работы способ изложения решения, так же, как и используемые обозначения, могут быть различными – такими, к каким студенты привыкли при проведении практических занятий.
4.2 Методические указания по разделу «Определение оптимальных параметров
экономической системы путем математического моделирования»
На первом этапе следует по статистическим данным найти оценки неизвестных параметров параболической корреляционной зависимости средних переменных издержек от объема выпуска:
Оценки параметров обозначаются символами 
. Студентам разрешается находить эти оценки, как аналитически, так и используя специальные программы на ЭВМ.
Необходимые основы теории корреляционной зависимости и аналитический метод нахождения оценок приведены в приложении 2.
Для нахождения оценок с помощью ЭВМ следует составить уравнение множественной линейной регрессии:
.
В качестве предиктора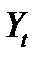 
используются статистические данные средних переменных издержек 
, а в качестве регрессоров 
и 
- значения 
и 
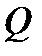. С помощью надстройки «Пакет анализа», входящей в состав табличного процессора Excel, по статистическим данным проводится идентификация данного уравнения и находятся оценки коэффициентов 
. Применение данной надстройки, для студентов, владеющих азами работы с Excel, не вызывает трудностей. Процедура применения описана в учебнике «Теория вероятностей и математическая статистика. Компьютерно - ориентированный курс» [2], а также может быть изучена на практических занятиях.
В результате аналитических расчетов или, проводя идентификацию уравнения регрессии с помощью ЭВМ, студент получает оценки . В дальнейшем, эти оценки используются в качестве приближенных значений коэффициентов . Заключительная часть работы опирается на исследование функции прибыли:
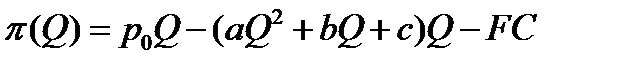для 
.
.
Поскольку все параметры данной функции теперь известны, студент, используя методы, известные из курса математического анализа, исследует данную функцию на экстремум. Эти методы описаны в учебном пособии «Математика в экономике и управлении» [1]. Должна быть найдена точка максимума, соответствующая неотрицательному значению 
. Обязательным является доказательство того, что найденная точка экстремума является именно точкой максимума. Это доказательство можно провести по первому или по второму достаточному признаку точки максимума.
В результате должен быть найден оптимальный объем выпуска 
рассматриваемой фирмы в условных единицах и ее максимальная прибыль 
в условных денежных единицах.
Приложение 1
