Метод Рунге-Кутта
Студенты ФИРТ
Группа ПО
Преподаватель
Гадилова Ф.Г.
Уфа 2007 г.
Содержание
ВВЕДЕНИЕ……………………………………………………………………………..…3
ГЛАВА 1. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
1.1. СУТЬ МЕТОДА РУНГЕ-КУТТА…………………………………………5
1.2. НАЗНАЧЕНИЕ И ОБЛАСТЬ ПРИМЕНЕНИЯ…………………………10
ГЛАВА 2. ПРАКТИЧЕСКАЯ ЧАСТЬ
2.1. ПОСТАНОВКА ЗАДАЧИ И РАЗРАБОТКА АЛГОРИТМА РЕШЕНИЯ ЗАДАЧИ…………………………………………………………………..……….11
2.2. ВЫБОР СОСТАВА ТЕХНИЧЕСКИХ И ПРОГРАММНЫХ СРЕДСТВ…………………………………………………………………...……...16
2.3. ВЫЗОВ И ЗАГРУЗКА ПРОГРАММЫ…………………….………….…...17
2.4. ТЕСТИРОВАНИЕ ПРОГРАММЫ……………………………………...…18
ЗАКЛЮЧЕНИЕ………………………………………………………………...…………19
ЛИТЕРАТУРА………………………………………………………………….…………20
ПРИЛОЖЕНИЯ:
ПРИЛОЖЕНИЕ№1 (ЛИСТИНГ ПРОГРАММЫ)
Введение
Целью курсовой работы является: написать программу для нахождения приближенного решения обыкновенного дифференциального уравнения y’=f(x,y), y(a)=y0 методом Рунге-Кутта пятого порядка на отрезке [a,b] с заданным постоянным шагом h.
Для достижения данной цели необходимо выполнить следующие задачи:
1. Рассмотреть суть метода Рунге-Кутта.
2. Назначение и область применения.
3. Протестировать программу.
Данная задача относится к численным методам. Необходимо найти решение обыкновенного дифференциального уравнения с постоянным шагом h.
Для решения задачи будет использоваться язык программирования Turbo Pascal 7.0, так как этот язык позволяет работать с математическими формулами, проводить различного рода математические операции и действия. Turbo Pascal фирмы Borland является расширением стандарта языка и содержит интегрированную среду, данного ускоряющую и облегчающую процесс разработки программ. В языке программирования Turbo Pascal 7.0 используется типизированный адресный оператор, открытые массивы и строки, что предоставляет пользователю дополнительные возможности при решении математических задач. В математических задачах часто требуется реализовать численные методы, экспериментально исследовать условие и скорость сходимости методов. В условии задачи, как правило, дается основная идея каждого метода (Эйлера, Рунге-Кутта и т.д.).
Вычисление функции и ее производной, используемой в задаче, рекомендуется оформлять в виде подпрограмм, так, чтобы можно было представлять любую функцию, не меняя самой программы. Погрешность, начальное условие и параметр алгоритма задаются вводом. Там, где это возможно, рекомендуется тестировать алгоритм на примерах, для которых известно или может быть найдено аналитически точное решение.
Глава 1.
Суть метода Рунге-Кутта
Метод Рунге-Кутта включает в себя несколько других таких как: метод Эйлера и метод Эйлера – Коши.
Методы Рунге-Кутта обладают следующими свойствами:
1. Эти методы являются одноступенчатыми: чтобы найти уm+1, нужна
информация о предыдущей точке xm,ym.
2. Они согласуются с рядом Тейлора вплоть до членов порядка hp, где степень р различна для различных методов и называется порядковым номером или порядком метода.
3. Они не требуют вычисления производных отf (x,y),а требуютвычисления самой функции.
Рассмотрим сначала геометрическое построение и выведем некоторые формулы на основе геометрических аналогий. После этого мы подтвердим полученные результаты аналитически. (Аналитический метод, применяется которого дает решение дифференциального уравнения в виде аналитического выражения; Графический метод, дающий приближенное решение в виде графика; Численный метод, когда искомая функция получается в виде таблицы.)
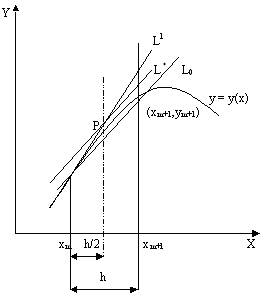
Предположим, нам известна точка xm,ym на искомой кривой. Тогда мы можем провести прямую линию с тангенсом угла наклона у¢m=f(xm,ym), которая пройдет через точку xm,ym. Это построение показано на рис.1, где кривая представляет собой точное, но конечно неизвестное решение уравнения, а прямая линия L1 построена так, как это только что описано.
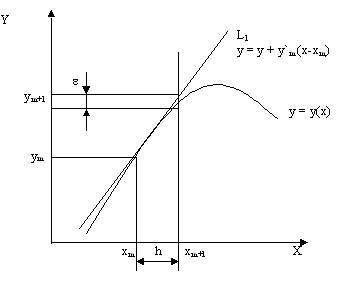
Тогда следующей точкой решения можно считать ту, где прямая L1 пересечет ординату, проведенную через точку x=xm+1=xm+h.
Уравнение прямой L1 выглядит так: y=ym+y¢m(x-xm) так как y¢=f(xm,ym) и кроме того, xm+1=xm+h тогда уравнение примет вид
ym+1=ym+h*f(xm,ym) 1.1.
Ошибка при x=xm+1 показана в виде отрезка е. Очевидно, найденное таким образом приближенное значение согласуется с разложением в ряд Тейлора вплоть до членов порядка h, так что ошибка ограничения равна et=Кh2
Заметим, что хотя точка на рис.1 была показана на кривой, в действительности ym является приближенным значением и не лежит точно на кривой.
Формула 1.1 описывает метод Эйлера, один из самых старых и широко известных методов численного интегрирования дифференциальных уравнений. Отметим, что метод Эйлера является одним из методов Рунге-Кутта первого порядка.
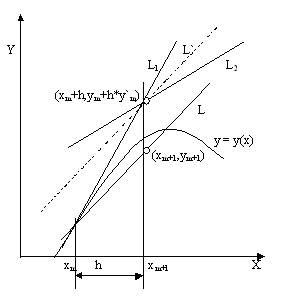
Рассмотрим исправленный метод Эйлера и модификационный метод Эйлера. В исправленном методе Эйлера мы находим средний тангенс угла наклона касательной для двух точек: xm,ym и xm+h,ym+hy¢m. Последняя точка есть та самая, которая в методе Эйлера обозначалась xm+1,ym+1. Геометрический процесс нахождения точки xm+1,ym+1 можно проследить по рис.2. С помощью метода Эйлера находится точка xm+h,ym+hy¢m, лежащая на прямой L1. В этой точке снова вычисляется тангенс, дает прямую L. Наконец, через точку xm,ym мы проводим прямую L, параллельную L. Точка, в которой прямая L пересечется с ординатой, восстановленной из x=xm+1=xm+h, и будет искомой точкой xm+1,ym+1.
Тангенс угла наклона прямой L и прямой L равен
Ф(xm,ym,h)=½[f(xm,ym)+f(xm+h,ym+y¢mh)] 1.2.
где y¢m=f(xm,ym) 1.3.
Уравнение линии L при этом записывается в виде
y=ym+(x-xm)Ф(xm,ym,h),
так что
ym+1=ym+hФ(xm,ym,h). 1.4.
Соотношения 1.2, 1.3, 1.4 описывают исправленный метод Эйлера.
Чтобы выяснить, насколько хорошо этот метод согласуется с разложением в ряд Тейлора, вспомним, что разложение в ряд функции f(x,y) можно записать следующим образом:
f(x,y)=f(xm,ym)+(x-xm)¶f/¶x+(y-ym)¶f/¶x+¼ 1.5.
где частные производные вычисляются при x=xm и y=ym.
Подставляя в формулу 1.5 x=xm+h и y=ym+hy¢m и используя выражение 1.3 для y¢m, получаем
f(xm+h,ym+hy¢m)=f+hfx+hffy+O(h2),
где снова функция f и ее производные вычисляются в точке xm,ym. Подставляя результат в 1.2 и производя необходимые преобразования, получаем
Ф(xm,ym,h)=f+h/2(fx+ffy)+O(h2).
Подставим полученное выражение в 1.4 и сравним с рядом Тейлора
ym+1=ym+hf+h2/2(fx+ffy)+O(h3).
Как видим, исправленный метод Эйлера согласуется с разложением в ряд Тейлора вплоть до членов степени h2, являясь, таким образом, методом Рунге-Кутты второго порядка.
Рассмотрим модификационный метод Эйлера. Рассмотрим рис.3 где первоначальное построение сделано так же, как и на рис.2. Но на этот раз мы берем точку, лежащую на пересечении этой прямой и ординатой x=x+h/2. На рисунке эта точка образована через Р, а ее ордината равна y=ym+(h/2)y¢m. Вычислим тангенс угла наклона касательной в этой точке
Ф(xm,ym,h)=f+(xm+h/2,ym+h/2*y¢m), 1.6.
где y¢m=f(xm,ym) 1.7.
Прямая с таким наклоном, проходящая через Р, обозначена через L*. Вслед за тем, мы проводим через точку xm,ym прямую параллельную L*, и обозначаем ее через L0. Пересечение этой прямой с ординатой x=xm+h и даст искомую точку xm+1,ym+1. Уравнение прямой можно записать в виде y=ym+(x-xm)Ф(xm,ym,h),
где Ф задается формулой 1.6. Поэтому
ym+1=ym+hФ(xm,ym,h)1.8.
Соотношения 1.6, 1.7, 1.8 описывают так называемый модификационный метод Эйлера и является еще одним методом Рунге-Кутта второго порядка. Обобщим оба метода. Заметим, что оба метода описываются формулами вида
ym+1=ym+hФ(xm,ym,h) 1.9.
и в обоих случаях Ф имеет вид
Ф(xm,ym,h)=a1f(xm,ym)+a2f(xm+b1h,ym+b2hy¢m), 1.10.
где y¢m=f(xm,ym) 1.11.
В частности, для исправленного метода Эйлера
a1=a2=1/2;
b1=b2=1.