Вопросы теории упругих волн
Источник м/б: пунктом взрыва или невзрывным источником.
Области изменен в упруг среде г/п: 1)область разрушен и вытеснен г/п; 2)обл-ть трещиноватости (радиальная, тангенсальная)- ограничив-сярадиусом пластичной деформации Rпл. За пределами этой зоны частицы среды после прекращен действия силы восстанавл свое первоначальн положение, т.е. остаточн деформац не накаплив-ся; 3)зона пластичн деформации. В этой зоне остаточн деформац нет. Во 2 и 3 области набл-ся остаточн деформац.
Св-ва г/п сохранять объемы или форму в рез-те действия внешн силы наз упругими деформац. Упр деформ не ограничив-ся по радиусу распростран упруг волн. С деформац связано напряжение, кот приходится на единицу поперечн сечения. Сила, действующая в упругом теле на единицу площади поперечн сечения наз напряжением. Напряжения Р м/б представлены в виде 2-х составляющих: 1)кот направлены по нормали Рп. С Рп связана деформац объема (мен-ся объем паралелепипеда); 2)касательное напряжен РΘ, кот опр-ет деформац сдвига(формы).
Рассмотрим:
1.Внутри тела действует Рп
Fn – внешн сила; ΔL/L – относит продольн удлинение; ΔD/D – относит поперечн сила.
Pn = Fn/S = E·ΔL/L, где Е – модуль продольного ратяжен (модуль Юнга). Е хар-ет сопротивл г/п растяжению или сжатию. Е = [Н/м2] или [дин/см2]. Для осадочн пород Е=(0,03÷9)·1011 [дин/см2], для пород фундамента Е = (3÷16)·1011[дин/см2].
М/у относит удлинен и поперечн сжатием завис-ть: ΔD/D = υ·ΔL/L, где υ – коэфф Пуассона (модуль поперечн сжатия). υ = (0,18÷0,5)-для осад пород и (0,19÷0,3)-для пород фундамента.
υ – безразмерная величина.
2.Рассмотрим напряжен в упругих средах – это касат напряжен. С ним связана деформ сдвига.
К кубу приложили силу под различн углами, и он изменил свою форму.
Θ – угод сдвига.
Θ ≈ tgΘ = Δх/х
РΘ = μ·Θ, где μ-модуль сдвига (или сопротивл г/п сдвигу). μ -это первая константа,
λ-вторая упругая константа.
Константы исп-ют для хар-ки волн в упругих средах.
Вывод: С каждым видом деформации объема(или формы) связано образован упруг волн 2.Образован продольн и поперечн волн
дорисовать
При возникновен Pn будет образовыв-ся в упруг среде продольн волна типа Р. Рассматривая перемещен частиц среды, вызванное деформац объема можно выделить 2 области в упругих средах, кот чередуются в процессе распростран волны продольного типа: область сжатия(объем уменьш) и область растяжен (объем увелич).
Скорость распростран прод волны: 
C РΘ связано образован поперечн волны. Она связана с деформац сдвига. Мен-ся форма элементарн параллелепипеда. Нарис рисунок
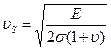
Св-ва поперечн волны:
1)поглощается жидкостями и газами, распростран-ся в тв фазах г/п (исп-ся при прямых поисках нефти и газа);
2)поляризация поперечн волны. Поляризация – вектор, кот меняет свое направлен в процессе распростр волны.
Вывод: Прод волна в упруг средах распростр-ся первой, S – второй. Глубинность S незначительна 3.Поверхностные волны.
Волны, распространяющиеся вдоль границы раздела воздух-земля и в верхнем приповерхностном слое. Характерная особенность они не распределяются в нижн полупростр-во, и не несут информации о глубинном строении земн коры, и явл-ся волнами-помехами.
1)Волна Релея R Рис
Возникает на границе раздела воздух-земля. Зависит от V распределения в верхнем слое.Ее особенность – перемещение частиц среды по эллиптическим орбитам. VR =0,9VS. Волна в процессе распространен быстро теряет энергию. В связи с интенсивным поглощением и незначит удалением от источника влияние этой волны не проявл-ся. Наиболее опасн участки влияния волны вблизи источника, где возможно наложение поверхностн волны на полезную.
2)Волна Лява, L.
Распространяется в верхнем маломощном приповерхностном слое, для кот характерны низкая скорость распростр поперечн волны. L относят к типу поперечн волн, т.к. происходит многократное отражен от верхн и нижн границы пласта. Скорость распростр L: 0,9VS1< VL<0,9VS2, где VS1<< VS2.
3)Звуковая волна
Образуется при взрыве, распростр по воздуху.
VЗВ.В »330 м/с
Она оказывает влияние при регистрации.
Общей характеристикой всех 3 волн является их низко- частотный состав.
Принципы геометрич сейсмики.
1)Гюйгенса
Любая точка, взятая на пов-ти фронта упругой волны (изохроны) явл-ся элементарным источником колебаний. 2 рисунка.
Если среда однород и изотропна, то скорость не мен-ся. Чтобы построить другие изохроны, зададим несколоко точек и рассчит радиус ΔR элементарного фронта волны на тот интервал времени, кот нам нужен ΔR=Δt·ν.
При анизотропн среде, ν ≠ const. Выдел-ся участки, в пределах кот скорость есть величина постоянная ΔRi=Δt·νi и рассчитыв-ся радиусы для каждого участка.
2)Принцип Ферма (принцип наименьшего времени). 2 рисунка
Луч – направление распространения волны. Луч направлен под 900 к изохроне. По Ферма: время движения по лучу минимальное. Часто лучи представл искривленными линиями.
Рисунок2 ν ≠ const.
Вторичные волны.
Рассмотрим двухслойную среду, в которой ν1≠ ν2. Падающая волна представлена Р (продольной волной). В точке А падения луча на границу раздела образуется 4 вторичных волны. Согласно принципу Гюйгенса данная точка является элементарным источникомколебаний одновременно в обеих средах. А так как любой источник вызывает образование как продольных так и поперечных волн, то две образующиеся волны будут относится к ……………..
Р11 – продольная отраженная волна; Р1S1 – поперечная отраженная волна; Р12 – проходящая продольная волна; Р1S2 – проходящая поперечн волна. Из группы вторичных волн выделим монотипные волны (волны, одинаков по типу с падающ волной - Р11 и Р12) и обменные - Р1S1 и Р1S2.
6.Закон отражения (з-н Снеллиуса). Рис.
Координате т.А соотв-ет х, т.е. А мен-ся в завис-ти от х.
На рис. О- источник, В-приемник, α1-угол падения, α2-угол отражения.
Падающая волна отраж-ся со скоростью ν1, отраженная ν2.
Согласно принципу Ферма время распространения волны по лучу минимально, следоват-но продифференцируем время dt/dx и приравняем его к 0.
Т.о. закон Снеллиуса следующ:
З-н Снеллиуса в общем виде характеризуетраспростр обменных отраженных волн (Р1S1, S1 Р1).
Для монотипной волны ν1=ν2, следоват-но sinα1=sinα2, → α1=α2.
К волнам типа Р11 относ-ся Р1221, Р123321 и т.д.
