Портфолио оформляется на электронном и бумажном носителях.
– объём презентаций не должен превышать 20 слайдов. Презентации сохранять в формате Power Point 2003 (.ppt);
– размер фото не более 100 кб, расширение не менее 800 х 600, видео – не более 200 мб;
– текстовые документы представляются в формате Word 2003 (doc.);
– параметры текстового редактора: поля – верхнее, нижнее – 2.0 см, левое – 3.0 см, правое – 1 см, шрифт Times New Roman, высота 14, межстрочный интервал полуторный, выравнивание по ширине, красная строка 1,25 см;
– документы, содержащие подписи и печати, сканируются в формате JPG или PDF, отсканированный текст, подписи и печати должны читаться без затруднений в масштабе 1:1;
– в текстах не допускается сокращение названий и наименований;
– все страницы нумеруются (нумерация начинается с титульного листа, номер на первой странице не ставится), номер страницы ставится в центре нижней части страницы, в колонтитуле на каждой странице указываются фамилия, имя и отчество студента.
Портфолио на бумажном носителе формируется в одной папке-накопителе с файлами.
3. Требования к презентации и защите портфолио:
Защита портфолио проводится в несколько этапов:
3.1. Презентация портфолио.
3.2. Ответы на вопросы по существу представленных документов.
3.3. Обсуждение результатов защиты членами экспертной группы.
3.4. Доведение до студента выводов и рекомендаций экспертной группы.
Презентация портфолио – форма аттестационного испытания, в ходе которого студент представляет экспертной комиссии свидетельства результатов образовательной деятельности в форме структурированного портфолио. Для презентации портфолио студенту отводится 10-15 минут. В ходе презентации он должен обосновать, как представленные материалы свидетельствуют о его профессиональной компетенции.
Качество презентации при защите портфолио оценивается по следующим показателям:
- соответствие содержания презентации содержанию портфолио;
- выделение основных результатов образовательной деятельности студента;
- качество изложения материала.
2.4. Пакет экзаменатора[6]
| ПАКЕТ ЭКЗАМЕНАТОРА | ||
| 1 семестр | ||
| ЭКЗАМЕНАЦИОННЫЕ ВОПРОСЫ | ||
| 1. Определители второго порядка. Определители третьего порядка. Свойства определителей. 2. Минор матрицы. Алгебраическое дополнение матрицы. 3. Матрицы. Сложение матриц. 4. Матрицы. Умножение матрицы на действительное число. Умножение матриц. 5. Правило Крамера. 6. Обратная матрица. 7. Уравнение прямой с угловым коэффициентом. Уравнение прямой, проходящей через две данные точки. 8. Уравнение прямой в отрезках. Общее уравнение прямой. 9. Понятие вектора. Линейные операции над векторами. 10. Скалярное произведение векторов. Выражение скалярного произведения через координаты векторов. 11. Определение векторного произведения. Выражение векторного произведения через координаты векторов. 12. Определение и геометрический смысл смешанного произведения векторов. 13. Линии второго порядка. 14. Определение числовой последовательности. Ограниченные и неограниченные последовательности. 15. Бесконечно большие и бесконечно малые последовательности. 16. Определение предела последовательности. Основные свойства сходящихся последовательностей. 17. Определение монотонных последовательностей. Признак сходимости монотонных последовательностей. 18. Определение предела функции. Свойства пределов. 19. Понятие производной. Правила дифференцирования. 20.Правило вычисления производной сложной функции. 21. Понятие дифференциала. 22. Производные и дифференциалы высших порядков. 23. Теорема Ферма. 24. Правила Лопиталя. 25. Признак монотонности функции. 26. Точки экстремума. Необходимое условие локального экстремума. Достаточное условие экстремума. 27. Направление выпуклости графика функции. Достаточное условие выпуклости функции. 28. Необходимое и достаточное условие точки перегиба. 29. Асимптоты графика функции. 30. Понятие первообразной. 31. Понятие неопределенного интеграла. Свойства неопределенного интеграла. 32. Определение определенного интеграла. Основные свойства. 33. Формула Ньютона – Лейбница. 34. Метод интегрирования по частям. 35. Геометрический смысл определенного интеграла. | ||
| ПРАКТИЧЕСКИЕ ЗАДАНИЯ К ЭКЗАМЕНУ | ||
1. Даны матрицы А, B. 1) Найти матрицу 2А-В.
  2. Найти определитель матрицы А.
2. Найти определитель матрицы А.
 3. 1) Найти матрицу А∙В.
3. 1) Найти матрицу А∙В.
  4. Найти матрицу D∙C.
4. Найти матрицу D∙C.
  5. Решить систему уравнений методом Гаусса:
5. Решить систему уравнений методом Гаусса:
 6. Решить систему уравнений по правилу Крамера:
6. Решить систему уравнений по правилу Крамера:
 7. Составить уравнение прямой, отсекающей на оси Oy отрезок b = 3 и образующий с осью Ox угол равный 45o.
8. Написать каноническое уравнение эллипса, если известно, что расстояние между фокусами равно 8, а малая полуось b = 3.
9. Вычислить предел:
7. Составить уравнение прямой, отсекающей на оси Oy отрезок b = 3 и образующий с осью Ox угол равный 45o.
8. Написать каноническое уравнение эллипса, если известно, что расстояние между фокусами равно 8, а малая полуось b = 3.
9. Вычислить предел: 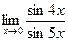 . .  10. Вычислить предел:
10. Вычислить предел:  .
11. Вычислить предел: .
11. Вычислить предел: 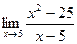 .
12. Вычислить предел: .
12. Вычислить предел:  . .  13. Найти производную функции:
13. Найти производную функции:  .
14. Найти производную функции: .
14. Найти производную функции: 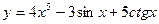 .
15. Найти производную функции: .
15. Найти производную функции:  .
16. Найти производную функции: .
16. Найти производную функции:  .
17. Найти производную второго от функции: .
17. Найти производную второго от функции:  18. Найти производную второго порядка от функции:
18. Найти производную второго порядка от функции:  .
19. Найти дифференциал функции: .
19. Найти дифференциал функции: 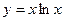 .
20. Найти дифференциал функции: .
20. Найти дифференциал функции: 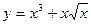 .
21. Найти максимумы и минимумы функции: .
21. Найти максимумы и минимумы функции: 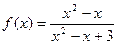 .
22. Найти максимумы и минимумы функции: .
22. Найти максимумы и минимумы функции:  .
23. Найти интервалы выпуклости и точки перегиба графика функции: .
23. Найти интервалы выпуклости и точки перегиба графика функции:  .
24. Найти интервалы выпуклости и точки перегиба графика функции: .
24. Найти интервалы выпуклости и точки перегиба графика функции: 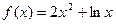 25. Найти неопределенный интеграл:
25. Найти неопределенный интеграл:  . .  26. Найти неопределенный интеграл:
26. Найти неопределенный интеграл: 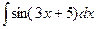 .
27. Найти неопределенный интеграл: .
27. Найти неопределенный интеграл:  .
28. Найти неопределенный интеграл: .
28. Найти неопределенный интеграл:  .
29. Вычислить определенный интеграл: .
29. Вычислить определенный интеграл: 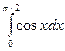 .
30. Вычислить определенный интеграл: .
30. Вычислить определенный интеграл:  .
31. Вычислить определенный интеграл: .
31. Вычислить определенный интеграл:  .
32. Вычислить определенный интеграл: .
32. Вычислить определенный интеграл:  .
33. Вычислить определенный интеграл: .
33. Вычислить определенный интеграл: 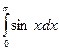 .
34. Найти площадь фигуры, ограниченной линиями: .
34. Найти площадь фигуры, ограниченной линиями:  . .
| ||
| 2 семестр | ||
| ЭКЗАМЕНАЦИОННЫЕ ВОПРОСЫ | ||
| 1. Функция двух переменных. Область определения функции, множество значений функции. 2. Предел и непрерывность функции двух переменных. 3. Частные производные функции. 4. Производные сложных функций. 5. Дифференциал функции двух переменных. 6. Частные производные высших порядков. 7. Дифференциалы высших порядков. 8. Определение двойного интеграла, его свойства. Определение повторного интеграла. 9. Приложения двойных интегралов. 10. Определение числового ряда, остатка ряда. 11. Свойства рядов. 12. Необходимое условие сходимости ряда. 13. Признак сравнения. 14. Признак Даламбера. 15. Радикальный и интегральный признаки Коши. 16. Определение знакочередующихся рядов, знакопеременных рядов. Признак Лейбница. 17. Определение абсолютной и условной сходимости произвольных числовых рядов. 18. Определение функционального ряда, степенного ряда. 19. Ряд Тейлора. 20. Ряд Фурье. 21. Определение радиуса сходимости ряда и области сходимости. 22. Теорема Абеля. 23. Дифференциальное уравнение. Общее и частное решение дифференциального уравнения. 24. Уравнение с разделяющимися переменными. 25. Линейные однородные и неоднородные дифференциальные уравнения первого порядка. 26. Линейные однородные и неоднородные дифференциальные уравнения второго порядка. 27. Дифференциальные уравнения, допускающие понижение степеней. 28. Определение комплексно числа. Геометрическое представление комплексных чисел. 29. Алгебраическая, тригонометрическая и показательная форма комплексного числа. 30. Действия над комплексными числами. 31. Тождество Эйлера. | ||
| ПРАКТИЧЕСКИЕ ЗАДАНИЯ К ЭКЗАМЕНУ | ||
1. Вычислить предел:  .
2. Вычислить предел: .
2. Вычислить предел:  .
3. Вычислить предел: .
3. Вычислить предел:  .
4. Найти частные производные первого порядка от функции: .
4. Найти частные производные первого порядка от функции:  .
5. Найти частные производные первого порядка от функции: .
5. Найти частные производные первого порядка от функции:  .
6. Найти частные производные второго порядка от функции: .
6. Найти частные производные второго порядка от функции:  .
7. Найти частные производные второго порядка от функции: .
7. Найти частные производные второго порядка от функции:  .
8. Найти дифференциал функции: .
8. Найти дифференциал функции:  .
9. Найти дифференциал функции: .
9. Найти дифференциал функции:  .
10. Вычислить двойной интеграл по прямоугольнику D: .
10. Вычислить двойной интеграл по прямоугольнику D:  .
11. Вычислить двойной интеграл по прямоугольнику D: .
11. Вычислить двойной интеграл по прямоугольнику D:  .
12. Вычислить двойной интеграл по области G: .
12. Вычислить двойной интеграл по области G:  .
13. Вычислить двойной интеграл по области G: .
13. Вычислить двойной интеграл по области G: 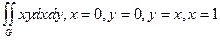 .
14. Исследовать сходимость ряда: .
14. Исследовать сходимость ряда:  .
15. Исследовать сходимость ряда: .
15. Исследовать сходимость ряда:  .
16. Исследовать сходимость ряда: .
16. Исследовать сходимость ряда:  .
17.Исследовать сходимость ряда: .
17.Исследовать сходимость ряда:  .
18. Исследовать на абсолютную и условную сходимость ряд: .
18. Исследовать на абсолютную и условную сходимость ряд:  .
19. Исследовать на абсолютную и условную сходимость ряд: .
19. Исследовать на абсолютную и условную сходимость ряд: 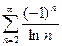 .
20. Найти радиус и интервал сходимости ряда и исследовать его сходимость на границах интервала: .
20. Найти радиус и интервал сходимости ряда и исследовать его сходимость на границах интервала: 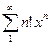 .
21. Найти радиус и интервал сходимости ряда и исследовать его сходимость на границах интервала: .
21. Найти радиус и интервал сходимости ряда и исследовать его сходимость на границах интервала:  .
22. Найти общие решения уравнения: .
22. Найти общие решения уравнения:  .
23. Найти общие решения уравнения: .
23. Найти общие решения уравнения:  .
24. Найти частные решения уравнения: .
24. Найти частные решения уравнения:  .
25. Найти частные решения уравнения: .
25. Найти частные решения уравнения:  .
26. Найти частные решения уравнения: .
26. Найти частные решения уравнения:  .
27. Записать комплексное число .
27. Записать комплексное число 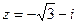 в тригонометрической форме.
28. Найти аргумент комплексного числа в тригонометрической форме.
28. Найти аргумент комплексного числа  .
29. Записать комплексное число .
29. Записать комплексное число  в тригонометрической форме.
30. Записать комплексное число в тригонометрической форме.
30. Записать комплексное число  в тригонометрической форме. в тригонометрической форме.
| ||
| Результаты освоения (объекты оценки) | Критерии оценки результата (в соответствии с разделом 1 «Паспорт комплекта контрольно-оценочных средств) | Отметка о выполнении |
| Уметь: Производить операции над матрицами и определителями; решать системы линейных уравнений; производить действия с векторами; решать задачи, используя уравнения прямых и кривых второго порядка на плоскости; вычислять пределы. вычислять производные и дифференциалы; находить неопределенные интегралы и вычислять определенные интегралы; исследовать на сходимость числовые ряды, разлагать элементарные функции в ряд Тейлора; находить частные производные и дифференциалы функций нескольких переменных; вычислять двойные интегралы; решать обыкновенные дифференциальные уравнения; пользоваться основными понятиями теории комплексных чисел. | Находит определитель матрицы, обратную матрицу, выполняет операции над матрицами. Решает системы уравнений методом Гаусса и Крамера. Проводит действия над векторами, находит скалярное, векторное и смешанное произведение. Вычисляет производные и дифференциалы. Находит неопределенные интегралы и вычисляет определенные интегралы. Исследует на сходимость числовые ряды, разлагает элементарные функции в ряд Тейлора. Находит частные производные и дифференциалы функций нескольких переменных. Приводит двойные интегралы к повторным, вычисляет двойные интегралы. Решает обыкновенные дифференциальные уравнения. Выполняет действия над комплексными числами в алгебраической, тригонометрической и показательной форме. | |
| Знать: Основные понятия и методы линейной алгебры; основные понятия и методы аналитической геометрии; основные понятия и методы математического анализа; основные понятия и методы теории комплексных чисел. | Знает основные понятия и методы линейной алгебры. Знает основные понятия и методы аналитической геометрии. Знает основные понятия и методы математического анализа. Знает основные понятия и методы теории комплексных чисел. | |
| Условия выполнения задания 1. Место выполнения задания: кабинет математики. 2. Максимальное время выполнения задания: ___ 45 ____ мин. 3. Вы можете воспользоваться таблицами постоянных величин. |
3. Критерии оценивания:
Тестов
«5» - 100 % выполнения задания
«4» - 99 – 70 % выполнения задания
«3» - 69 -50 % выполнения задания
«2» - менее 50 % выполнения задания
Оценка 5 ("отлично") ставится студентам, которые при ответе:
- обнаруживают всестороннее систематическое и глубокое знание программного материала;
- демонстрируют знание современной учебной и научной литературы;
- способны творчески применять знание теории к решению задач;
- владеют понятийным аппаратом;
- демонстрируют способность к анализу и сопоставлению различных подходов к решению заявленной проблематики;
- подтверждают теоретические постулаты примерами из практики.
Оценка «хорошо»:
Ответы на поставленные вопросы излагаются систематизировано и последовательно. Материал излагается уверенно. Демонстрируется умение анализировать материал, однако не все выводы носят аргументированный и доказательный характер. Соблюдаются нормы литературной речи.
Оценка "хорошо" ставится студенту за правильные ответы на вопросы, знание основных характеристик раскрываемых категорий в рамках рекомендованного учебниками и положений, данных на лекциях. Обязательно понимание взаимосвязей между явлениями и процессами, знание основных закономерностей.
Оценка 4 ("хорошо") ставится студентам, которые при ответе:
- обнаруживают твёрдое знание программного материала;
- усвоили основную и наиболее значимую дополнительную литературу;
- способны применять знание теории к решению задач профессионального характера;
- допускают отдельные погрешности и неточности при ответе.
Оценка «удовлетворительно»:
Допускаются нарушения в последовательности изложения. Демонстрируются поверхностные знания вопроса. Имеются затруднения с выводами. Допускаются нарушения норм литературной речи.
Оценка 3 ("удовлетворительно") ставится студентам, которые при ответе:
- в основном знают программный материал в объёме, необходимом для предстоящей работы по профессии;
- в целом усвоили основную литературу;
- допускают существенные погрешности в ответе на вопросы.
Оценка "удовлетворительно" предполагает ответ только в рамках лекционного курса, который показывает знание сущности основных категорий теории.. Как правило, такой ответ краток, приводимые формулировки являются недостаточно четкими, нечетки, в ответах допускаются неточности. Положительная оценка может быть поставлена при условии понимания студентом сущности основных категорий по рассматриваемому и дополнительным вопросам.
Оценка «неудовлетворительно»:
Материал излагается непоследовательно, сбивчиво, не представляет определенной системы знаний. Имеются заметные нарушения норм литературной речи.
Оценка "неудовлетворительно" предполагает, что студент не разобрался с основными вопросами изученных в процессе обучения, не понимает сущности процессов и явлений, не может ответить на простые вопросы типа "что это такое?" и "почему существует это явление?". Оценка "неудовлетворительно" ставится также студенту, списавшему ответы на вопросы и читающему эти ответы преподавателю, не отрываясь от текста, а просьба объяснить или уточнить прочитанный таким образом материал по существу остается без ответа.
Оценка 2 ("неудовлетворительно") ставится студентам, которые при ответе:
- обнаруживают значительные пробелы в знаниях основного программного материала;
- допускают принципиальные ошибки в ответе на вопросы экзаменационного билета;
- демонстрируют незнание теории и практики.
| Содержание учебного материала по программе УД | |||||||||||
| Контрольная работа по теме: «Матрицы и определители. Системы линейных уравнений». | |||||||||||
| Зачет по теме: «Векторы. Операции над векторами». | З1 | З2 | З3 | У1 | У2 | У3 | |||||
| Зачет по теме: «Прямая на плоскости. Кривые второго порядка». | + | + | + | + | + | ||||||
| Зачет по теме: «Теория пределов. Непрерывность». | + | + | + | + | + | ||||||
| Зачет по теме: «Дифференциальное исчисление функции одной переменной». | + | + | + | + | + | + | |||||
| Контрольная работа по темам: «Дифференциальное исчисление функции одной переменной. Интегральное исчисление функции». | + | + | + | + | + | ||||||
| Зачет по теме: «Дифференциальное исчисление функции нескольких действительных переменных» | + | + | + | + | + | + | |||||
| Контрольная работа по темам: «Дифференциальное исчисление функции нескольких действительных переменных. Интегральное исчисление функции нескольких переменных». | + | + | + | + | + | + | |||||
| Зачет по теме: «Теория рядов». | + | + | + | + | + | ||||||
| Зачет по теме: «Обыкновенные дифференциальные уравнения». | + | + | + | + | + | + | |||||
| Зачет по теме: «Основы теории комплексных чисел». | + | + | + | + | + | ||||||
[1] Рекомендуется согласовать комплект контрольно-оценочных средств с представителями профессионального сообщества (работников и или специалистов по профилю получаемого образования, руководителей организаций отрасли, профессиональных экспертов и др.) и приложить документы, подтверждающие факт согласования
[2] Указываются коды и наименования результатов обучения в соответствии с программой учебной дисциплины (знания, умения) или профессионального модуля (общие, профессиональные компетенции, умения, знания, практический опыт). Подробнее см. разъяснения по разработке КОС
[3] Критерии указываются, если необходимы для того чтобы впоследствии эксперты могли дать ответ в экспертном листе, используя дуальную систему: «выполнил – не выполнил»; «да-нет» и т.п. Чаще всего помимо показателей требуются критерии при разработке оценочных средств по программам СПО.
[4] № задания указывается, если предусмотрен.
[6] Пакет экзаменатора может быть сформирован как по всем заданиям (если оценивание проводится единовременно и / или объем заданий невелик), так и по каждому заданию (если оценивание рассредоточено во времени и проводится по накопительной системе и / или объем заданий велик). Приведен макет для одного задания.
[i] Правила заполнения таблицы см. в разъяснениях по разработке КОС






