59.1. Основные способы геометрического нивелирования
В главе 5, при рассмотрении вопросов поверок нивелиров (§49), говорилось о способах геометрического нивелирования «из середины» и «вперёд». Рассмотрим несколько подробнее каждый их этих способов.
Нивелирование из середины. Для определения превышения между точками А и В нивелир устанавливают посредине между ними (рис. 6.2 а), т.е. обеспечивают равенство плеч LA = LB на станции. Разность отсчётов на заднюю точку А (З) и переднюю точку В (П) определяет искомое превышение передней точки над задней, если оцифровка шкал используемых реек возрастает от их основания:
h = З – П. (6.2)
Рис. 6.2. Способы геометрического нивелирования:
нивелирование из середины (а); нивелирование вперёд (б); последовательное (сложное) нивелирование (в).
Если известна высота точки А (НА), то
НВ = НА + h. (6.3)
При нивелировании вперёд (рис. 6.2 б) нивелир размещают в точке А, измеряют его высоту i = З и определяют превышение по формуле
h = i – П = З – П, (6.4)
т.е. по той же формуле (6.2), а высоту точки В – по формуле (6.3).
При нивелировании вперёд нивелир может размещаться непосредственно в точке А (проекция окуляра зрительной трубы совпадает с положением точки А) либо вблизи этой точки на расстоянии, позволяющем получить чёткое изображение шкалы рейки.
Кроме рассмотренных выше способов геометрического нивелирования существует способ последовательного или сложного нивелирования, в котором могут быть одновременно использованы как способ нивелироваия из середины, так и способ нивелирования вперёд (рис. 6.2 в).
Этот способ применяют при передаче высот на сравнительно большие расстояния (при трассировании), при нивелировании рек, геофизических профилей, создании высотного обоснования и в других случаях.
Для привязки нивелирного хода геометрического нивелирования значительной длины целесообразно иметь в начале и конце хода нивелирные реперы: РА (начальный репер) и РВ (конечный репер). В этом случае нивелирование можно выполнять в ходе одного направления.
Точки хода, отсчёты на которые по рейке берут на соседних двух станциях, называют связующими (точки 1, 2, …, n - 1). Расстояние между связующими точками, имеющими нумерацию, часто определено, например, 100 м, 50 м. Связующие точки закрепляют на местности кольями либо выбирают устойчивые точки местности, на которые при нескольких постановках можно однозначно устанавливать рейку.
59.2. Оценка точности нивелирного хода при последовательном нивелировании
Рассмотрим передачу высот по нивелирному ходу от начального репера на конечный репер при числе станций n:
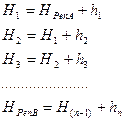(6.5)
Если сложить уравнения (6.5) и исключить из них в суммарном уравнении одинаковые слагаемые в правой и левой частях, то получим
. (6.6)
Разность высот исходных реперов хода
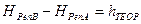(6.7)
называется теоретическим превышением. Значение суммы превышений хода представляет практическое превышение hПР, которое может содержать погрешность (невязку в превышениях), равную
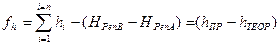. (6.8)
В зависимости от назначения нивелирного хода соответствующими инструкциями установлены допуски на величину невязки, зависящие от длины L хода либо от фактического числа станций n при его проведении. Так, для технического нивелирного хода
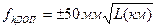(6.9)
или
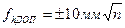, (6.10)
если число станций n (штативов) на 1 км хода превышает 25.
Условие, которое характеризует качественное выполнение нивелирных работ, записывается в виде неравенства
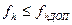. (6.11)
Если на местности в конце хода не имеется возможности выполнить привязку к реперу (репер расположен слишком далеко), то нивелирование выполняют в прямом и обратном направлениях. Обратный ход прокладывают обычно только по связующим точкам либо по другому кратчайшему пути по другим связующим точкам. В этом случае, поскольку НРепА = НРепВ, теоретическая сумма превышений hТЕОР = 0, как это следует из (6.7). Невязка же в превышениях будет равна
. (6.12)
Для определения допустимого значения невязки используют те же формулы (6.9) и (6.10) с учетом фактически пройденного расстояния в прямом и обратном направлениях либо фактического числа станций.
