Эйлеровым циклом (путем) графа называется цикл (путь), содержащий все ребра графа ровно один раз. Граф, обладающий эйлеровым циклом, называется эйлеровым графом.
Граф G обладает эйлеровым циклом с концами  и
и  тогда и только тогда, когда G – связный и
тогда и только тогда, когда G – связный и  ,
,  – единственные его вершины нечетной степени.
– единственные его вершины нечетной степени.
Граф G является эйлеровым тогда и только тогда, когда G – связный и все его вершины имеют четную степень.
Гамильтоновым циклом (путем) графа G называется цикл (путь), проходящий через каждую вершину G в точности по одному разу. Граф, обладающий гамильтоновым циклом, называется гамильтоновым.
Эйлеров путь (эйлерова цепь) в графе — это путь, проходящий по всем рёбрам графа и притом только по одному разу. (ср.Гамильтонов путь)
Эйлеров цикл — это эйлеров путь, являющийся циклом.
Гамильтонов путь — простой путь в графе, содержащий все вершины графа ровно по одному разу.
Гамильтонов цикл — простой цикл в графе, содержащий все вершины графа ровно по одному разу.
Теорема Понтрягина-Куратовского.
Граф планарен тогда и только тогда, когда он не содержит подграфов, гомеоморфных  или или  . .
|
|
Заметим, что из планарности графа следует планарность гомеморфного графа и наоборот. В самом деле, пусть 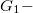 плоский граф. Если добавить на нужных ребрах вершины степени плоский граф. Если добавить на нужных ребрах вершины степени  и удалить некотрые вершины степени и удалить некотрые вершины степени  в в  , получим укладку гомеоморфного графа , получим укладку гомеоморфного графа  . Таким образом, доказательство достаточности следует из непланарности . Таким образом, доказательство достаточности следует из непланарности  и и  .
Докажем неоходимость. От противного: пусть существует непланарный граф, который не содержит подграфов, гомеоморфных .
Докажем неоходимость. От противного: пусть существует непланарный граф, который не содержит подграфов, гомеоморфных  или или  . Пусть . Пусть 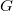 — такой граф с наименьшим возможным числом рёбер, не содержащий изолированных вершин. — такой граф с наименьшим возможным числом рёбер, не содержащий изолированных вершин.
|
Деревья. Основные понятия и определения.
Дерево — это связный ациклический граф. Связность означает наличие путей между любой парой вершин, ацикличность — отсутствие циклов и то, что между парами вершин имеется только по одному пути.
Граф без цикла называется лесом. Вершины степени1 в дереве называются листьями.
Корневое дерево - это ориентированное дерево, в котором можно выделить вершины трех видов: корень, листья (другое их название: терминальные вершины) и остальные вершины (нетерминальные); причем должны выполняться два обязательных условия:
из листьев не выходит ни одна дуга; из других вершин может выходить сколько угодно дуг;
в корень не заходит ни одна дуга; во все остальные вершины заходит ровно по одной дуге.
Традиционно в математике и в родственных ей науках (в том числе и в теоретическом программировании) деревья "растут" вниз головой: это делается просто для удобства наращивания листьев в случае необходимости. Таким образом, на рисунках корень дерева оказывается самой верхней вершиной, а листья - самыми нижними.
Предок вершины v - это вершина, из которой исходит дуга, заходящая в вершину v. Потомок вершины v - это вершина, в которую заходит дуга, исходящая из вершины v. В этих терминах можно дать другие определения понятиям корень и лист: у корня нет предков, у листа нет потомков.
Бинарное дерево - это корневое дерево, каждая вершина которого имеет не более двух потомков. В таком случае иногда говорят о левом потомке и правом потомке для текущей вершины.
Высота корневого дерева - это максимальное количество дуг, отделяющих листья от корня. Если дерево не взвешенное, то его высота - это просто расстояние от корня до самого удаленного листа.






