Агрегатное состояние вещества. Поведение молекул в разных агрегатных состояниях. Энергия одной молекулы газа

Агрега́тное состоя́ние вещества (лат. aggrego 'присоединяю') — состояние одного и того же вещества в определённом интервале температур и давлений, характеризующееся определёнными, неизменными в пределах указанных интервалов, качественными свойствами:

· способностью (твёрдое тело) или неспособностью (жидкость, газ, плазма) сохранять объём и форму,

· наличием или отсутствием дальнего (твёрдое тело) и ближнего порядка (жидкость), и другими свойствами.

Изменение агрегатного состояния может сопровождаться скачкообразным изменением свободной энергии, энтропии,плотности и других физических величин.^[1]

Традиционно выделяют три агрегатных состояния: твёрдое тело, жидкость и газ. К агрегатным состояниям принято причислять также плазму^[2], в которую переходят газы при повышении температуры и фиксированном давлении. Существуют и другие агрегатные состояния, например, жидкие кристаллы или конденсат Бозе — Эйнштейна.

Отличительной особенностью является отсутствие резкой границы перехода к плазменному состоянию.

Определения агрегатных состояний не всегда являются строгими. Так, существуют аморфные тела, сохраняющие структуру жидкости и обладающие небольшой текучестью и способностью сохранять форму; жидкие кристаллы текучи, но при этом обладают некоторыми свойствами твёрдых тел, в частности, могут поляризовать проходящее через них электромагнитное излучение.

Для описания различных состояний в физике используется более широкое понятие термодинамической фазы. Явления, описывающие переходы от одной фазы к другой, называют критическими явлениями.

ТВЕРДОЕ С микроскопической точки зрения твёрдые тела характерны тем, что молекулы или атомы в них в течение длительного времени сохраняют своё среднее положение неизменным, только совершая колебания с небольшой амплитудой вокруг них. В кристаллах средние положения атомов или молекул строго упорядочены. Кристаллы характеризуются пространственной периодичностью в расположении равновесных положений атомов, которая достигается наличием дальнего порядка и носит название кристаллической решётки. Естественная форма кристаллов — правильные многогранники. В аморфных телах атомы колеблются вокруг хаотически расположенных точек, у них отсутствует дальний порядок, но сохраняется ближний, при котором молекулы расположены согласованно на расстоянии, сравнимом с их размерами. Согласно классическим представлениям, устойчивым состоянием (с минимумом потенциальной энергии) твёрдого тела является кристаллическое

ЖИДКОСТЬ Молекулы жидкости не имеют определённого положения, но в то же время им недоступна полная свобода перемещений. Между ними существует притяжение, достаточно сильное, чтобы удержать их на близком расстоянии. Вещество в жидком состоянии существует в определённом интервале температур, ниже которого переходит в твёрдое состояние (происходит кристаллизация либо превращение в твердотельное аморфное состояние — стекло), выше — в газообразное (происходит испарение). Границы этого интервала зависят от давления. Как правило, вещество в жидком состоянии имеет только одну модификацию. (Наиболее важные исключения — это квантовые жидкости и жидкие кристаллы.) Поэтому в большинстве случаев жидкость является не только агрегатным состоянием, но и термодинамической фазой (жидкая фаза).

ГАЗ

С микроскопической точки зрения газ — это состояние вещества, в котором его отдельные молекулы взаимодействуют слабо и движутся хаотически. Взаимодействие между ними сводится к спорадическим столкновениям. Кинетическая энергия молекул превышает потенциальную. Подобно жидкостям, газы обладают текучестью и сопротивляются деформации. В отличие от жидкостей, газы не имеют фиксированного объёма и не образуют свободной поверхности, а стремятся заполнить весь доступный объём (например, сосуда). По химическим свойствам газы и их смеси весьма разнообразны — от малоактивных инертных газов до взрывчатых газовых смесей. Понятие «газ» иногда распространяют не только на совокупности атомов и молекул, но и на совокупности других частиц — фотонов, электронов, броуновских частиц, а также плазму. Некоторые вещества не имеют газообразного состояния.

ПЛАЗМА

Четвёртым агрегатным состоянием вещества часто называют плазму. Плазма является частично или полностью ионизованным газом и в равновесном состоянии обычно возникает при высокой температуре, от нескольких тысяч кельвинов и выше. В земных условиях плазма образуется в газовых разрядах. В общем, её свойства напоминают свойства газообразного состояния вещества, за исключением того факта, что для плазмы принципиальную роль играет электродинамика, то есть равноправным с ионами и электронами составляющей плазмы является электромагнитное поле.

Плазма — самое распространённое во Вселенной агрегатное состояние вещества. В этом состоянии находится вещество звёзд и вещество, наполняющее межпланетное, межзвёздное и межгалактическое пространство. Большая часть барионного вещества (по массе около 99,9 %) во Вселенной находится в состоянии плазмы

ЭНЕРГИЯ

Внутренняя энергия — это кинетическая энергия хаотического (теплового) движения частиц системы (молекул, атомов, ядер, электронов) и потенциальная энергия взаимодействия этих частиц.
Внутренняя энергия идеального газа есть сумма кинетических энергий его частиц (энергией взаимодействия частиц пренебрегаем).

Число степеней свободы — это число независимых переменных, полностью определяющих положение молекулы как системы атомов в пространстве.

Газ		одноатомный	двухатомный	трехатомный
Число степеней свободы	поступательных
вращательных	—
всего

Закон Больцмана о равномерном распределении энергии по степеням свободы молекулы:
На каждую степень свободы молекулы приходится в среднем одинаковая энергия
, где — постоянная Больцмана,
— абсолютная температура газа.

Таким образом, средняя кинетическая энергия одной молекулы газа
, где
— сумма числа поступательных, числа вращательных и удвоенного числа колебательных степеней свободы молекулы.
.
На колебательную степень свободы приходится вдвое большая энергия потому, что на нее приходится не только кинетическая энергия (как в случае поступательного и вращательного движений), но и потенциальная, причем средние значения кинетической и потенциальной энергий одинаковы.

Внутренняя энергия газа, содержащего частиц, количеством молей и массой :
.

8. внутренняя энергия газа U из чего она складывается связь с теплоемкостью и температурой

Внутренняя энергия — это кинетическая энергия хаотического (теплового) движения частиц системы (молекул, атомов, ядер, электронов) и потенциальная энергия взаимодействия этих частиц.

Согласно закону Джоуля, выведенному эмпирически, внутренняя энергия идеального газа не зависит от давления или объёма. Исходя из этого факта, можно получить выражение для изменения внутренней энергии идеального газа. По определению молярной теплоёмкости при постоянном объёме, . Так как внутренняя энергия идеального газа является функцией только от температуры, то

.

Эта же формула верна и для вычисления изменения внутренней энергии любого тела, но только в процессах при постоянном объёме (изохорных процессах); в общем случае 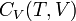является функцией и температуры, и объёма.

Если пренебречь изменением молярной теплоёмкости при изменении температуры, получим:

,

где — количество вещества, — изменение температуры.

Для идеального газа внутренняя энергия равна:

,

где - количество степеней свободы, - универсальная газовая постоянная.

ЭНТАЛЬПИЯ

Энтальпи́я, также тепловая функция и теплосодержание — термодинамический потенциал, характеризующий состояние системы в термодинамическом равновесии при выборе в качестве независимых переменных давления, энтропии и числа частиц.

Проще говоря, энтальпия — это та энергия, которая доступна для преобразования в теплоту при определенном постоянном давлении.

Если термомеханическую систему рассматривать как состоящую из макротела (газа) и поршня площадью S с грузом весом Р = pS, уравновешивающего давление газа р внутри сосуда, то такая система называется расширенной.

Энтальпия или энергия расширенной системы Е равна сумме внутренней энергии газа U и потенциальной энергии поршня с грузом E _пот = pSx = pV

Таким образом, энтальпия в данном состоянии представляет собой сумму внутренней энергии тела и работы, которую необходимо затратить, чтобы тело объёмом V ввести в окружающую среду, имеющую давление р и находящуюся с телом в равновесном состоянии. Энтальпия системы H — аналогично внутренней энергии и другим термодинамическим потенциалам — имеет вполне определенное значение для каждого состояния, т. е. является функцией состояния. Следовательно, в процессе изменения состояния

Изменение энтальпии (или Тепловой эффект химической реакции) не зависит от пути процесса, определяясь только начальным и конечным состоянием системы. Если система каким-либо путём возвращается в исходное состояние (круговой процесс), то изменение любого её параметра, являющегося функцией состояния, равно нулю, отсюда 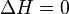, или же

Дифференциал энтальпии, выраженный в собственных переменных — через энтропию S и давление p:

Поскольку в квазиравновесных процессах 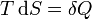— количество теплоты, подведенной к системе, отсюда вытекает физический смысл введения понятия энтальпии: ее изменение — это тепло, подведенное к системе в изобарическом процессе (при постоянном давлении). Практическое применение этой функции основано на том, что множество химических процессов в реальных или лабораторных условиях реализуются именно при постоянном (атмосферном) давлении, когда резервуар открыт. Так, энтальпия образования — количество энергии, которое выделяется или поглощается при образовании сложного вещества из простых веществ.

Все химические реакции сопровождаются выделением (экзотермические) или поглощением (эндотермические) тепла. Мерой теплоты реакции служит изменение энтальпии ΔН, которая соответствует теплообмену при постоянном давлении. В случае экзотермических реакций система теряет тепло и ΔН — величина отрицательная. В случае эндотермических реакций система поглощает тепло и ΔН — величина положительная.

Энтальпией системы удобно пользоваться в тех случаях, когда в качестве независимых переменных, определяющих состояние системы, выбирают давление р и температуру Т

В этом случае изменение энтальпии в изобарическом процессе практически удобно рассчитывать, зная теплоемкость при постоянном давлении (термохимический закон Кирхгофа):

При этом используется эмпирическое разложение теплоёмкости в ряд по степеням Т:

Энтальпия — величина аддитивная (экстенсивная), т. е. для сложной системы равна сумме энтальпий её независимых частей . Подобно другим термодинамическим потенциалам, энтальпия определяется с точностью до постоянного слагаемого, которому в термодинамике часто придают произвольные значения (например, при расчете и построении тепловых диаграмм). При наличии немеханических сил величина энтальпии системы равна

где — обобщённая сила; — обобщённая координата.

 

 

Инвариантная энтальпия в релятивистской термодинамике

При построении релятивистской термодинамики (с учетом специальной теории относительности) обычно наиболее удобным подходом является использование так называемой инвариантной энтальпии — для системы, находящейся в некотором сосуде.

При этом подходе температура определяется как лоренц-инвариант. Энтропия — также инвариант. Поскольку стенки влияют на систему, наиболее естественной независимой переменной является давление , в связи с чем в качестве термодинамического потенциала удобно брать именно энтальпию^[1].

Для такой системы «обычная» энтальпия и импульс системы 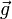образуют 4-вектор, и за определение инвариантной энтальпии, одинаковой во всех системах отсчёта, берётся инвариантная функция этого 4-вектора:

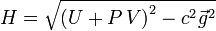
Основное уравнение релятивистской термодинамики записывается через дифференциал инвариантной энтальпии следующим образом:

Пользуясь этим уравнением, можно решить любой вопрос термодинамики движущихся систем, если известна функция .

ЭНТРОПИЯ

Энтропи́я (от др.-греч. ἐντροπία — поворот, превращение) — в естественных науках мера неупорядоченности системы, состоящей из многих элементов. В частности, в статистической физике — мера вероятности осуществления какого-либо макроскопического состояния; в теории информации — мера неопределённости какого-либо опыта (испытания), который может иметь разные исходы, а значит, и количество информации; в исторической науке, для экспликации феномена альтернативности истории (инвариантности и вариативности исторического процесса).

Энтропия в информатике — степень неполноты, неопределённости знаний.

Энтропия — мера неупорядоченности системы.

Явление, обратное энтропии, именуется негэнтропией.

Понятие энтропии впервые было введено Клаузиусом в термодинамике в 1865 году для определения меры необратимого рассеивания энергии, меры отклонения реального процесса от идеального. Определённая как сумма приведённых теплот, она является функцией состояния и остаётся постоянной при замкнутых обратимых процессах, тогда как в необратимых — её изменение всегда положительно.

,

где — приращение энтропии; — минимальная теплота, подведённая к системе; — абсолютная температура процесса.

· Термодинамическая энтропия — термодинамическая функция, характеризующая меру неупорядоченности термодинамической системы, то есть неоднородность расположения и движения её частиц.

Закон

Первое начало термодинамики — один из трёх основных законов термодинамики, представляет собой закон сохранения энергии для термодинамических систем.

Изменение полной энергии системы в квазистатическом процессе равно количеству теплоты , сообщённому системе, в сумме с изменением энергии, связанной с количеством вещества при химическом потенциале , и работы ^[3], совершённой над системой внешними силами иполями, за вычетом работы , совершённой самой системой против внешних сил

.

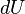Для элементарного количества теплоты , элементарной работы и малого приращения внутренней энергии первый закон термодинамики имеет вид:

.

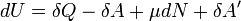Разделение работы на две части, одна из которых описывает работу, совершённую над системой, а вторая — работу, совершённую самой системой, подчёркивает, что эти работы могут быть совершены силами разной природы вследствие разных источников сил.

Важно заметить, что 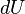и 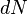являются полными дифференциалами, а и — нет.

Важным следствием первого закона термодинамики является утверждение о невозможности создания машины, способной совершать полезную работу без потребления энергии извне и без каких-либо изменений внутри самой машины. Такая гипотетическая машина получила название вечного двигателя (perpetuum mobile) первого рода. Многочисленные попытки создать такую машину неизменно заканчивались провалом. Любая машина может совершать положительную работу A над внешними телами только за счет получения некоторого количества теплоты Q от окружающих тел или уменьшения Δ U своей внутренней энергии.

12.

Используя понятие энтальпии, первый закон термодинамики можно записать в виде

 

При количественном анализе процессов часто используется математическая запись первого закона термодинамики через энтальпию:

, Дж,	(2.13)
, Дж / кг,	(2.14)
,	(2.15)
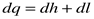,	(2.16)
.

13. Уравнение первого закона термодинамики для движущегося рабочего тела

Уравнение первого закона для единицы массы стационарного потока (т. е. потока, параметры которого в любом сечении со временем не изменяются) можно вывести с помощью модели, показанной на рис. 3.2.

Рис. 3.2. К выводу уравнения первого закона термодинамики для движущегося рабочего тела

Здесь поток получает теплоту dq, совершает техническую работу dl, а также работу за счет изменения его кинетической энергии d(w²/2) и работу против силы тяжести d(g*h) вследствие изменения его высоты над уровнем моря (h=h₂-h₁). Кроме того, имеет место работа вталкивания газа p₁*v₁ и выталкиванияp₂*v₂. Их разность l_пр=p₂*v₂-p₁*v₁ называют работой проталкивания. Учитывая сказанное можно записать закон сохранения энергии для движущегося рабочего тела

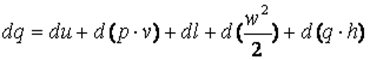
(3.9)

Здесьu – внутренняя энергия рабочего тела.

Так как по определению u+p*v=i, полученное выражение можно переписать следующим образом