; где
Px – интенсивность давления, передающегося на основание (реактивный отпор грунта в т. Х)
Zx – величина перемещения в т. Х (зависит от жесткости балок, характера распределения нагрузки, размеров балки и деформируемости основания
Сz – коэффициент постели
Впервые этот метод был применён при расчете шпал под ж/дор., тогда считали, что Сz = f (грунта), но потом выяснилось, что Сz = f (грунта и ширины подошвы фундамента)
Px = 
; Сz = ; Zx = см
Из сопромата известно уравнение, описывающее изгиб балки:
; 
;
ЗначениеРх заменяем исходнойформулой:
Решая это уравнение мы найдем Zx:
; А1, А2, А3, А4 - произвольные постоянные, определяемые из
начальных параметров.
В конечном итоге находим Сz и Рх , а следовательно Мх и Qx .
Решение этой задачи во многих случаях приведено в табличной форме в зависимости от конструкции фундаментов (Справочник проектировщика).
; 
Расчет балок по методу общих упругих деформаций.
(Гипотеза упругого полупространства)
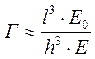; где Г - гибкость балки;
l - полудлина балки;
h – высота балки;
Е – модуль упругости материала балки;
Е0 – модуль общей деформации грунта.
Г<1 - абсолютно жёсткая балка Для всех случаев составлены таблицы
1<Г>10 - жёсткая балка (метод Горбунова-Посадова)
Г>10 - гибкая балка
Часто при расчете гибких фундаментов (особенно если жесткость балки применима)- переходят к решению задач по методу Жемочкина Б.Н. (Исследование приемов строительной механики для решения статически неопределимых систем).
Метод Жемочника для расчета фундаментных балок
на упругом основании.
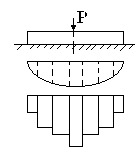В основу метода положены следующие допущения:
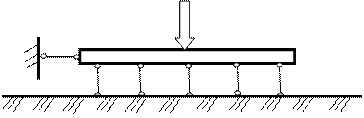
1. Действительная криволинейная эпюра
распределения давлений под подошвой
балки заменяется ступенчатой
Распределение давлений на ширине балки
также принимаются равномерным.
2. Между балкой и сжимаемым основанием предполагаются жесткие шарниры опирающиеся стержни, воспринимающие усилия от балки и равномерно распределяющие это усилие на основание.
4. Условие совместимости работы балки и основания и удовлетворяются равенством прогиба балки и осадки основания в месте закрепления опорного стержня yi=Si.
Этот метод является универсальным и позволяет решать любые задачи с любой степенью сложности.
 | |||||||||
 | |||||||||
 | |||||||||
| |||||||||
 |
Задача решается смешанным методом.
- единичное перемещение по направлению "к" связи от воздействия "i" связи
- единичное перемещение, вызванное осадкой основания
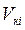- единичное перемещение, вызванное прогибом балки
; 
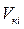-находятся обычно по таблицам
Решив систему уравнений и найдя Xi, определяют величины реактивных давлений Рi, соответствующих ширине принятых участков ступенчатой эпюры (см. допущение № 1):
 |
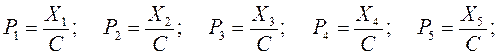Затем с использованием метода сечений строят эпюры изгибающих моментов M, а по ним окончательно определяют сечение балки и ее армирование
Область применения:
1. При хороших (плотных) грунтах.
2. Для расчета плит (днища емкостей).
3. При глубоком залегании скалы.
