Функция F (x) называется первообразной функции f (x) на некотором промежутке 
, если F (x) дифференцируема на промежутке X и для всех 
выполняется 
Например, 
— первообразная для 
.
Если F (x) – одна из первообразных функции f (x) на промежутке X, то любая другая ее первообразная имеет вид 
, где C – произвольная постоянная.
Совокупность всех первообразных функции f (x) называется неопределенным интегралом от функции f (x). Обозначение: 
. Функция f (x) называется подынтегральной функцией, f (x) dx – подынтегральное выражение, x – переменная интегрирования.
Операция нахождения неопределённого интеграла от данной функции называется интегрированием этой функции.
Достаточное условие существования неопределённых интегралов. Всякая непрерывная на множестве X функция имеет на этом множестве первообразную, а значит, неопределенный интеграл.
Геометрическая трактовка неопределённого интеграла. Если , то уравнение y=F(x)+C задает однопараметрическое семейство линий на плоскости Оxy, каждая из которых называется интегральной линией для функции f(x). Все интегральные линии для y=f(x) имеют одинаковую форму и не пересекаются, т.к. получаются друг из друга сдвигом по оси Оу.
Свойства неопределённого интеграла.
Свойство 1 (о производной неопределённого интеграла).
Производная неопределённого интеграла по переменной интегрирования равна подынтегральной функции: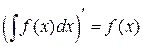 
.
Свойство 2 (о рядом стоящих знаках интеграла и дифференциала).
Рядом стоящие знаки дифференциала и интеграла взаимно уничтожаются:
а) 
(дифференциал от неопределенного интеграла равен подынтегральному выражению);
б) 
.
Свойство 3 (о линейности неопределённого интеграла по подынтегральной функции).
а) Неопределённый интеграл от суммы двух или нескольких функций равен сумме неопределённых интегралов от каждой функции:
;
б) Постоянный множитель можно выносить за знак неопределённого интеграла:
.
----------------------------------------------------------------------------------------------------------------
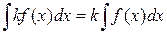Понятие неопределённого интеграла. Непосредственное интегрирование.
Метод подстановок. Стр.1
Таблица основных интегралов.
1. 
.
2. 
, 
.
3. 
, 
.
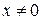4. 
.
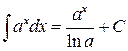4′. 
.
5. 
.
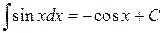6. 
.
7. 
.
8. 
.
9. 
, 
.
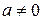9′. 
.
10. 
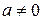, – «высокий логарифм”.
11. 
, .
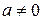11′. 
.
12. 
, 
– «длинный логарифм”.
Вычисление неопределённых интегралов с использованием их свойств и таблицы интегралов называется непосредственным или табличным интегрированием.
Пример 1. Путем непосредственного интегрирования найти неопределенный интеграл 
.
Решение. 
----------------------------------------------------------------------------------------------------------------
Понятие неопределённого интеграла. Непосредственное интегрирование.
Метод подстановок. Стр.2
Замечание: при вычислении суммы нескольких интегралов одну произвольную постоянную интегрирования следует добавлять только в конце после того, как закончено все интегрирование.
Пример 2. Путем непосредственного интегрирования найти неопределенный интеграл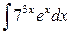 
.
Решение. 
Пример 3. Путем непосредственного интегрирования найти неопределенный интеграл 
.
Решение. 
Пример 4. Путем непосредственного интегрирования найти неопределенный интеграл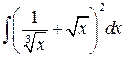 
.
Решение. 
Во многих случаях введение новой переменной интегрирования позволяет свести нахождение данного интеграла к нахождению табличного, т.е. перейти к непосредственному интегрированию. Такой метод называется методом подстановки или методом замены переменной.
Правило замены переменной интегрирования. Пусть требуется вычислить 
.Переменную интегрирования х можно заменить на другую переменную t, выполнив подстановку 
или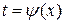 
. При этом в исходном интеграле нужно всё подынтегральное выражение пересчитать через переменную t и её дифференциал, учитывая определение дифференциала функции: 
или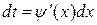 
. В результате подстановки получим, что 
.
После вычисления интеграла по переменной t нужно вернуться к переменной х, выполнив обратную замену. Выполненная подстановка считается эффективной, если получившийся интеграл по новой переменной интегрирования окажется проще исходного.
----------------------------------------------------------------------------------------------------------------
Понятие неопределённого интеграла. Непосредственное интегрирование.
Метод подстановок. Стр.3
Пример 5. Вычислить интеграл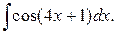 
Решение.
.
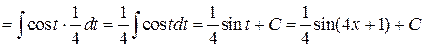Пример 6. Вычислить интеграл 
Решение.
.
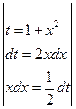
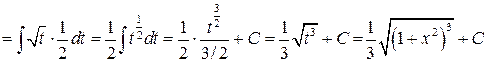