Особенностью преобразователей этого вида заключается в том, что напряжение на его выходе непосредственно соответствует пиковому (амплитудному) значению напряжения, поданного на вход преобразователя. Преобразователь должен содержать элемент, запоминающий пиковое значение напряжения. Обычно это конденсатор, заряжаемый через диод до пикового значения.
Необходимо отметить, что амплитудные преобразователи – самые широкополосные преобразователи напряжения переменного тока в напряжение постоянного тока. Далее приведены схемы часто встречающихся преобразователей: с открытым и закрытым входом.
Для всех преобразователей должны выполняться условия:
- постоянная времени цепи заряда конденсатора τз=RiC (здесь Ri- внутренне сопротивление диода) должна быть много меньше постоянной времени τр=RC цепи разряда конденсатора;
- значение τз £ 1/fв= Тв (период самого высокочастотного измеряемого напряжения);
- значение τр >>1/fн= Тн (период самого низкочастотного напряжения).
а) преобразователь пикового (амплитудного) значения с открытым входом
Рассмотрим работу преобразователя когда к нему приложено синусоидальное напряжение 
. В начальный момент времени 
полностью приложено к диоду поскольку 
>> Сд диода.
Ri
u(t)
+
При первой положительной полуволне в цепи диода возникает большой импульс тока, который подзаряжает конденсатор. При каждой положительной полуволне синусоидального напряжения u(t) конденсатор подзаряжается через внутреннее сопротивление диода Ri.
Учитывая, что постоянная времени заряда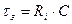 
<< 
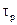, напряжение на конденсаторе 
через несколько периодов практически достигнет пикового значения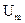 
. Очевидно, что из-за разряда конденсатора С напряжение на нем всегда будет Uc<Um. Относительную погрешность преобразования можно вычислить по формуле:
.
Из формулы видно, что погрешность преобразования уменьшается при увеличении значений R и C. Однако следует отметить, что чрезмерное увеличение сопротивления резистора R приведет к значительному росту τр и преобразователь станет инерционным (при изменении u(t) на входе напряжение на конденсаторе будет долго оставаться неизменным). Увеличение емкости конденсатора С так же приведет к недопустимому увеличению постоянных времени τр и τз.
При подаче на вход рассматриваемого преобразователя напряжения с постоянной составляющей u(t)=U0+Umsinwt его выходное напряжение будет определяться суммарным воздействием постоянной и переменной (амплитудной) составляющих: Uпр= U0+Um.
б) преобразователь пикового (амплитудного) значения с закрытым входом
Рассмотрим работу преобразователя при подаче гармонического сигнала u(t)=Umsinwt.
За несколько положительных полупериодов конденсатор С заряжается через диод почти до значения 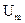.Разряжается конденсатор через резистор достаточно большого номинала 
, как и в преобразователе с открытым входом.
Основное различие состоит в том, что выходным является напряжение UR, представляющее собой алгебраическую сумму напряжений на конденсаторе С и входного напряжения. После подавления переменной составляющей этого сигнала с помощью фильтра ФНЧ на индикаторном устройстве ИУ будет отображаться постоянная составляющая U0.
 |
Рис.15.
Наличие сглаживающего фильтра отличает данную схему от амплитудного преобразователя с открытым входом, где он не нужен.
Если на вход подается напряжение с постоянной составляющей U0, то в зависимости от полярности включения диода преобразователь будет реагировать либо на положительное Um+, либо на отрицательное Um- значение переменной составляющей относительно линии среднего значения U0.
При измерении напряжения без постоянной составляющей А- преобразователи с открытым и закрытым входом дают одно и тоже значение.
Многие пиковые вольтметры хотя и измеряют пиковое значение, но градуируются в среднеквадратических значениях для гармонических сигналов 
. Поэтому для измерения среднеквадратического значения сигнала произвольной формы необходимо воспользоваться формулой: 
.
