Задача 3
Имеются следующие данные за год по заводам одной промышленной компании:
| Завод | Среднее число рабочих, чел. | Основные фонды, млн руб. | Продукция, млн руб. | Завод | Среднее число рабочих, чел. | Основные фонды, млн руб. | Продукция, млн руб. |
На основании приведенных данных составьте групповую таблицу зависимости выработки на одного рабочего от величины заводов по числу рабочих. Число групп – три.
Решение:
Выработка на одного работающего количества произведенной продукции:
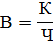
Выработка для каждого завода:
| Завод | Среднее число рабочих, чел. | Основные фонды, млн руб. | Продукция, млн руб. | Выработка на одного работающего |
| 0,43 | ||||
| 0,45 | ||||
| 0,43 | ||||
| 0,67 | ||||
| 0,82 | ||||
| 1,04 | ||||
| 0,91 | ||||
| 1,15 | ||||
| 1,14 | ||||
| 1,21 | ||||
| 1,41 | ||||
| 1,35 | ||||
| 1,50 | ||||
| 1,47 | ||||
| 1,58 |
Величина интервала: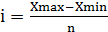 
, где Xmax и Xmin– максимальное и минимальное значения признака, т.е. число рабочих, а n–число групп. 
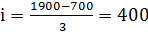- получили 3 группы:
1гр. - от 700 до 1100 рабочих
2 гр. – от 1100 до 1500 рабочих
3 гр. – от1500 до 1900 рабочих
Рабочая таблица:
| Номер группы | Номера заводов | Среднее число рабочих, чел. | Основные фонды, млн руб. | Продукция, млн руб. | Выработка на одного рабочего |
| 0,43 | |||||
| 0,43 | |||||
| 0,45 | |||||
| 0,67 | |||||
| 0,82 | |||||
| 0,91 | |||||
| ИТОГО | 3,70 | ||||
| 1,04 | |||||
| 1,15 | |||||
| 1,14 | |||||
| 1,21 | |||||
| ИТОГО | 4,55 | ||||
| 1,35 | |||||
| 1,41 | |||||
| 1,47 | |||||
| 1,50 | |||||
| 1,58 | |||||
| ИТОГО | 4,55 |
По данным рабочей таблицы составляем аналитическую группировку:
| Номер группы | Количество заводов | Группы заводов по числу рабочих | Основные фонды в среднем на один завод, млн руб. | Продукция в среднем на один завод, млн руб. | Выработка на одного рабочего в среднем на один завод |
| 700-1100 | 563,33 | 0,62 | |||
| 1100-1500 | 1537,50 | 1,14 | |||
| 1500-1900 | 1,46 |
Вывод: С увеличением количества рабочих увеличиваются основные фонды и выработка на одного рабочего.
Задача 10
Планом промышленного предприятия предусматривалось снижение затрат на 1 руб. товарной продукции на 4 %, фактически затраты возросли на 2%. Вычислите относительную величину выполнения плана.
Решение:
ОВВП=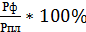 
Относительная велич. вып. пл. =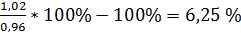 
Ответ: План по снижению затрат не выполнен, так как фактический уровень превысил запланированный на 6,25%
Задача 17
Вычислите среднемесячный % брака по заводу за второй квартал по данным:
| Показатель | апрель | май | июнь |
| Выпуск годной продукции, тыс.руб. | |||
| Брак, в % к годной продукции | 1,5 | 1,2 | 1,0 |
Решение:
Среднемесячный процент брака =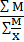 
; М=х*f; f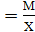 
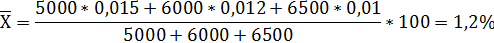
Ответ: Среднемесячный процент брака за второй квартал равен 1,2%
Задача 24
Определите среднюю выработку рабочего за смену и среднеквадратическое отклонение, моду и медиану, используя следующие данные:
| Выработано деталей рабочим в смену, шт. | ||||
| Число рабочих с данной выработкой, чел. |
Решение:
Средняя выработка рабочего за смену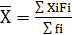 
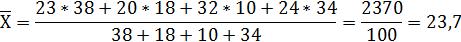
Среднеквадратичное отклонение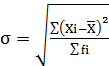 
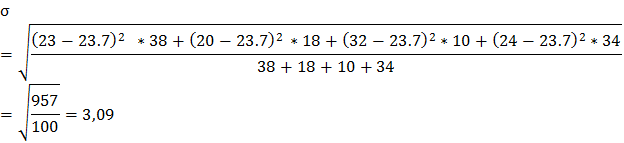
Мода и медиана:
Упорядочим последовательность по выработке
| Выработано деталей рабочим в смену, шт. | ||||
| Число рабочих с данной выработкой, чел. |
Средняя из двух величин (по формуле средней арифметической)
Me = (23+24)/2=23,5
Мода - значение признака (варианта), которое чаще всего встречается в данной совокупности, в данном случае это выработка 23 деталей.
Ответ: Me=23,5; Mo=23
Задача 31
По приведенным данным о выпуске продукции химическим предприятием по годам в сопоставимых ценах вычислить на постоянной и переменной базах сравнения абсолютный прирост, темпы роста и прироста, а также абсолютное значение 1 % прироста.
Рассчитать средний уровень ряда. Рассчитать при помощи метода скользящей средней за каждые три года среднегодовой выпуск продукции. Произвести аналитическое выравнивание ряда по прямой.
| Годы | ||||||
| Выпуск продукции, млн руб. | 79,2 | 110,8 |
Решение:
1. Рассчитываем средний уровень ряда:
40 + 50 + 60 + 66 + 79,2 + 110,8 = 406 / 6 = 67,7
2.Находимпри помощи метода скользящей средней среднегодовой выпуск продукции за каждые три года:
1. 40 + 50 + 60 = 150 / 3 = 50
2. 50 + 60 + 66 = 176 / 3 = 58,7
3. 60 + 66 + 79,2 = 205,2 / 3 = 68,4
4. 66 + 79,2 + 110,8 = 256 / 3 = 85,3
3. Проводим аналитическое выравнивание ряда по прямой.
Находим параметры уравнения методом наименьших квадратов.
Система уравнений МНК:
a0n + a1∑t = ∑y
a0∑t + a1∑t2 = ∑y • t
| t | y | t2 | y2 | ty |
| 79,2 | 6272,64 | 475,2 | ||
| 110,8 | 12276,64 | 775,6 | ||
| 30605,28 | 1834,8 |
Для наших данных система уравнений имеет вид:
6a0 + 23a1 = 406
23a0 + 115a1 = 1834,8
Из первого уравнения выражаем а0 и подставим во второе уравнение
Уравнение тренда:
y = 10,378 t + 27,886
Эмпирические коэффициенты тренда a и b являются лишь оценками теоретических коэффициентов βi, а само уравнение отражает лишь общую тенденцию в поведении рассматриваемых переменных.
Коэффициент тренда b = 10,378 показывает среднее изменение результативного показателя (в единицах измерения у) с изменением периода времени t на единицу его измерения. В данном примере с увеличением t на 1 единицу, y изменится в среднем на 10,378.
Для оценки качества параметров уравнения построим расчетную таблицу.
| t | Y | y(t) | (y-ycp)2 | (y-y(t))2 | (t-tp)2 |
| 38,26 | 765,44 | 3,02 | 8,03 | ||
| 48,64 | 312,11 | 1,85 | 3,36 | ||
| 59,02 | 58,78 | 0,96 | 0,69 | ||
| 69,4 | 2,78 | 11,53 | 0,0278 | ||
| 79,2 | 90,15 | 133,02 | 119,94 | 4,69 | |
| 110,8 | 100,53 | 1860,48 | 105,49 | 10,03 | |
| 3132,61 | 242,79 | 26,83 |
Анализ точности определения оценок параметров уравнения тренда.
Стандартная ошибка уравнения.
,
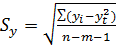где m = 1 - количество влияющих факторов в модели тренда.
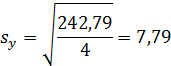
По таблице Стьюдента находим Tтабл
Tтабл (n-m-1;α/2) = (4;0,025) = 2,776
tp = 3,833 • 1% = 0,0383
Рассчитаем границы интервала, в котором будет сосредоточено 95% возможных значений Y при неограниченно большом числе наблюдений и t = 0,0383
(a + btp ± ε),
где
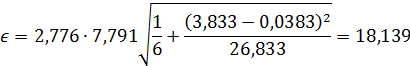
y(0,0383) = 10,378*0,0383 + 27,886 = 28,283
(28,283 - 18,139; 28.283 - 18,139)
(10,145;46,422)
Задача 38
Работа производственного объединения по добыче угля, в состав которого входят шахта и разрез, за месяц характеризуется следующими данными:
| Производственные подразделения | Объем добычи угля, тыс. т | Среднемесячная выработка на одного рабочего, т | ||
| базисный период | отчетный период | базисный период | отчетный период | |
| Шахта | ||||
| Разрез | 61,2 |
Определите:
1) натуральные индексы переменного и постоянного состава производительности труда (выработки) по объединению;
2) индекс влияния структурных сдвигов на средний уровень производительности труда;
3) какая часть абсолютного прироста добычи угля за период получена в результате изменения численности рабочих и какая – в результате роста производительности труда.
Решение:
индекс производительности труда переменного состава.
