Математическая статистика. Ее виды, особенности, задачи.
Математическая статистика – раздел математики, посвященный математическим методам обработки, систематизации и использования статичных данных для практических и научных целей.
Задачей этого раздела является разработка практических методов, регистрации, описания, анализ экспериментальных данных, получаемых в опытах с массовыми явлениями.
Особенностью статистики является изучение массовых, случайных явлений в условной неопределенности. Достоверность выводов зависит от числа объектов исследования. На основе анализов и прогнозов вырабатывается оптимальное решение.
Статистика подразделяется на:
- теоретическую (вырабатывает методы)
прикладную (общая, отраслевая (экономическая статистика, метеорологическая, медицинская))
Медицинская статистика:
- ст. рождаемости
- ст. заболеваемости
- ст. смертности
- ст. медицинских учреждений
Биологическая статистика (=биометрия) – включает статистические методы, используемые в различных биологических исследованиях (в цитологии, микробиологии).
Статистика:
- описательная (комплекс методов сбора, группировки данных и представления их в виде таблиц, графиков…)
- аналитическая (делает заключения, выводы с целью практического применения)
Основные понятия описательной статистики. Их характеристика
1. Генеральная совокупность – подлежащая изучению совокупность однородных элементов, которая характеризуется некоторым признаком. Например, нас интересует распространенность данного заболевания в определенном регионе, тогда генеральная совокупность, это все население региона. Если необходимо выразить мужчин и женщин отдельно по этому заболеванию, то получаем 2 генеральные совокупности.
Количество объектов, входящих в генеральную совокупность называется объемом генеральной совокупности (N)
Генеральная совокупность можно изучать по некоторой ее части.
2. Выборочная совокупность - часть генеральной совокупности, выбираемая для статистической обработки (выборка) (объем выборки -n). Свойства объектов выборки должны соответствовать свойствам генеральной совокупности.
Результаты исследования некоторого признака генеральной совокупности, будут более надежны, если выборку образовывать случайным образом. Элементы выборки берутся наугад. Каждый объект может попасть в выборку с одинаковой вероятностью. Главным вопросом является: как определить объем выборки, необходимой для получения необходимого результата.
3. Варианта – значение признака для каждого элемента выборки (х)
Признаки могут быть качественными и количественными
Количественные делятся на непрерывные (масса тела) и дискретные (количество волос)
Признак, имеющий значение от одного объекта к другому называется варьирующимся. Если количественный признак лежит в интервале – интервальный.
4. Частота – количество объектов с конкретным числовым значением признака
xi 35 36 37 38 39 40 41
ni (pi): 2 4 5 6 7 7 2
5. Частность или относительная частота – доля варианта с данным значением признака (ni/n)
Ряды распределения и способы их представления.
Ряд распределения – это последовательность качественных или количественных значений признака и частоты его встречаемости.
Ряд, составленного на основе качественного признака – атрибутивных количественного – вариационный.
Рассмотрим подробнее распределение количественного признака. Значение признака, записанное для всех элементов выборки в том порядке, в каком они были получены образуют простой (упорядоченный) статистический ряд.
1 2 3 4 5 6
170 165 171 165 163 174
Из данных видно: некоторые значения вариант повторяются. Для сокращения записи данные располагаются в упорядоченном виде с указанием частот. Такой ряд называется упорядоченным (=ранжированным).
ni 1 2 1 1 1 1
xi 163 165 160 171 174
Вариационные ряды могут быть непрерывными и дискретными
Способы представления рядов:
1. Табличный (см. выше)
2. Аналитический (с помощью формул)
3. Графический (строится на основании табличных данных)
Способы графического представления:
А) диаграмма в отрезках – совокупность вертикальных прямых /отрезков. Способ удобен для представления дискретных признаков при небольшом объеме совокупности.
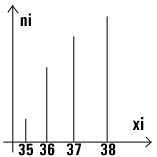
Б) гистограмма – совокупность прилегающих друг к другу прямоугольников. Способ используется для изображения. для интервального ряда. На оси Х откладываются интервалы значения варианта. На каждом из них (на основании) строят прямоугольник. Его высота зависит от частоты встречаемости данной величины.
В) полигон частот – ломаная линия, соединяющая точки, являющиеся серединами интервалов.
Г) Вариационные кривые в зависимости от значения распределения.
ni
Прямоугольное распределение объема совокупности
ni
Колоколообразное (= унимодальное)
ni
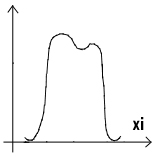Бимодальное
ni
Экспоненциальное
