Глава 4
Аналитическая геометрия на плоскости и в пространстве
Прямая на плоскости. Уравнение прямой с угловым коэффициентом. Общее уравнение прямой и его исследование
Общее уравнение прямой на плоскости
Определение 29.1: Под прямой линией будем понимать геометрическое место точек l такое, что для любых двух точек M  и M из данного множества вектор
и M из данного множества вектор  коллинеарен заданному ненулевому вектору
коллинеарен заданному ненулевому вектору  .
.
 (29.5)
(29.5)
и  (29.6)
(29.6)
ЗАДАЧА. Доказать, что если векторы  и
и  ортогональны некоторому вектору
ортогональны некоторому вектору  , то
, то 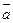 и
и  коллинеарные.
коллинеарные.
Определение 29.2: Уравнение (29.5) с условием (29.6) называется общим уравнением прямой линии на плоскости.
Определение 29.3: А вектор  называется нормальным вектором (или нормалью) к прямой l, заданной уравнением (29.5).
называется нормальным вектором (или нормалью) к прямой l, заданной уравнением (29.5).
Как уже было показано, вектор  , то есть
, то есть 
Исследование общего уравнения прямой на плоскости
 (29.9)
(29.9)
Уравнение прямой с угловым коэффициентом
 (29.10)
(29.10)

Определение 29.4: Поэтому уравнение (29.10) называется уравнение прямой с угловым коэффициентом (а множитель k- её угловым коэффициентом).
К уравнению 29.10 можно свести всякую прямую, не коллинеарную оси ординат (если  OY, то есть l
OY, то есть l  OX, то
OX, то 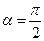 и
и  ).
).
Угол между двумя прямыми. Условие параллельности и перпендикулярности прямых
Случай уравнения прямых с угловыми коэффициентами
 |



|
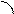



 (30.4)
(30.4)
 То есть угол между прямыми
То есть угол между прямыми  и
и  можно найти по формуле (30.4).
можно найти по формуле (30.4).
|
 и
и  .
.
1. Условие параллельности:  (см. черт. 30.2)
(см. черт. 30.2) 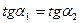
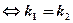 (30.5)
(30.5)
(и  , иначе
, иначе 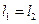 )
)
2. Условие перпендикулярности: 
 (см. чертеж 30.1)
(см. чертеж 30.1)  (см. равенство(30.4))
(см. равенство(30.4))  (30.6)
(30.6)
3. Точка пересечения прямых  и
и  .
.
Абсциссу точки пересечения прямых можно найти приравняв, правые части уравнений (30.1) и (30.2):

Решая уравнение (30.7), получим

А подставив полученную в (30.8) абсциссу точки пересечения прямых в уравнение (30.1) (или в (30.2)), найдем и ординату их точки пересечения:

 =
= 
Случай общего уравнения прямых линий
| |||
 | |||
 Пусть прямые
Пусть прямые  и
и  заданы уравнениями:
заданы уравнениями:





|
|


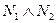
 (30.12)
(30.12)
Координаты точки пересечения прямых  и
и  можно найти, решая систему из двух линейных уравнений (30.10) и (30.11). По формулам Крамера (см. §8) имеем:
можно найти, решая систему из двух линейных уравнений (30.10) и (30.11). По формулам Крамера (см. §8) имеем:
|
 x=
x= 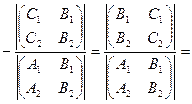

y= 

Для взаимного расположения прямых  и
и  рассмотрим матрицы:
рассмотрим матрицы:

 и
и 
1.  =
= 
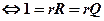 (30.14).
(30.14).
2.  ||
|| 

 (30.15)
(30.15)
3.  и
и  пересекаются в одной точке
пересекаются в одной точке 
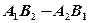 (30.16)
(30.16)
Условие перпендикулярности прямых  и
и  :
:
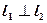
 =
=  (30.14)
(30.14)
( – нормаль к прямой
– нормаль к прямой  , а
, а  – нормаль к прямой
– нормаль к прямой  (см. чертёж 30.3))
(см. чертёж 30.3))
§31. Уравнение прямой на плоскости по двум точкам и «в отрезках»
31.1 Уравнение прямой проходящей через точку  и коллинеарной заданному вектору
и коллинеарной заданному вектору 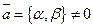
Её уравнение имеет вид  ,
,
или  (см. уравнение (29.4))
(см. уравнение (29.4))
31.2 Уравнение прямой проходящей через заданную точку  и ортогональной заданному вектору
и ортогональной заданному вектору 
 (см. уравнение (29.8)).
(см. уравнение (29.8)).
31.3 Уравнение прямой проходящей через две заданные точки  и
и 
Это уравнение имеет вид:
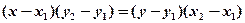 (31.1)
(31.1)
В случае  в (31.1) у можно выразить через x:
в (31.1) у можно выразить через x:
 (31.2)
(31.2)
А для  и
и  уравнение (31.1) можно записать следующим образом:
уравнение (31.1) можно записать следующим образом:

31.4 Уравнение прямой «в отрезках»
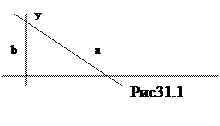 | |||
| |||
 (29.9)
(29.9)
Определение 31.1: Поэтому уравнение (29.9) называется уравнением прямой «в отрезках».





 l1
l1


