ЭЛЕКТРИЧЕСКОЙ НАГРУЗКИ
Цель работы
Исследование процесса нагрева электрического кабеля и трансформатора при изменяющейся во времени нагрузке и определение их расчетных нагрузок.
Теоретические сведения
Протекание тока нагрузки по элементу электрической сети приводит к его нагреву в результате потерь электроэнергии на активном сопротивлении. При нагреве проводников в первую очередь страдает изоляция, затем контактные соединения, а затем сами проводники. Поэтому для тех элементов системы электроснабжения, которые имеют изоляцию, нагревающуюся вместе с проводниками, предельно допустимая температура нагрева определяется изоляцией. В теории расчетных электрических нагрузок чаще используется температура перегрева проводника относительно окружающей среды, т.к. мощность, рассеиваемая с нагретого тела в окружающую среду, зависит от разности температур.
Различают три вида допустимой температуры перегрева:
· Длительно допустимая температура перегрева в нормальном режиме (νдд), соответствующая длительно допустимому току
,
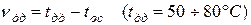где tдд = (50...80) °С – длительно допустимая температура нагрева для массовых видов изоляции (резина, пластмасса, бумага, масло); tос – температура окружающей среды;
· Допустимый перегрев при перегрузках (νп) в течение ограниченного времени (tп = 90...120 °С). При этом происходит ускоренное старение изоляции. Известно, так называемое, 8-градусное правило, заключающееся в том, что при превышении температуры перегрева на 8 градусов относительно νдд срок службы изоляции сокращается вдвое;
· Максимально допустимый кратковременный перегрев при коротких замыканиях ν max (tmax = 125...350 °С).
Процесс нагрева элемента электрической сети, например трехжильного кабеля, описывается уравнением теплового баланса
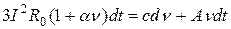(3.1)
где R0 – удельное сопротивление кабеля, Ом/км;
ν – перегрев кабеля относительно окружающей среды, °С;
α – температурный коэффициент увеличения сопротивления проводника, 1/°С;
с – удельная теплоемкость кабеля, Вт∙с/°С∙км;
А – коэффициент теплоотдачи, характеризующий отдачу тепла с поверхности 1 км кабеля. Вт/°С;
t – время, с.
Левая часть уравнения (3.1) представляет собой энергию, выделившуюся в кабеле за счет протекания тока величиной I за время dt. Первое слагаемое правой части – энергия, затраченная на повышение температуры кабеля на величину dν. Второе – энергия, рассеянная с поверхности кабеля за время dt при температуре перегрева кабеля относительно окружающей среды ν.
Коэффициент А возрастает с увеличением ν так же, как и возрастает величина (1+αν). Поэтому для упрощения дальнейших рассуждений можно принять α=0; А = Ао = const. Тогда уравнение (3.1) можно записать в упрощенной форме, разделив его на Аdt
,
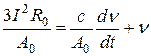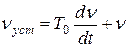, (3.2)
где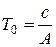 
– постоянная времени нагрева кабеля, с;
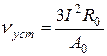– установившееся значение перегрева, °С. (3.3)
Решением уравнения (3.2) является зависимость перегрева от времени
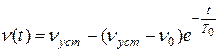, (3.4)
кривая которого для простейшего одноступенчатого графика тока приведена на рис.4.
Рис.4. График перегрева
При t≤0, I(t)=0, ν(t)=0. При 0 ≤ t≤ t1 по кабелю протекает ток I(t) = const и происходит нагрев кабеля от ν(t)=0 до νуст no экспоненте (3.4). Величина Т0 характеризует время нагрева кабеля от любой исходной температуры до νуст при условии отсутствия теплоотдачи с поверхности кабеля в окружающую среду. Величина νуст – температура перегрева, при достижении которой наступает тепловое равновесие: количество тепла, выделяемого в кабеле при протекании по нему тока равно количеству тепла, отдаваемого с поверхности кабеля в окружающую среду.
При t≥t1 ток в кабеле отключен, кабель охлаждается, температура перегрева уменьшается от νуст до нуля с той же постоянной времени Т0. Только в этом случае Т0 – время, в течение которого температура кабеля уменьшается до температуры окружающей среды при условии постоянства теплоотвода с поверхности кабеля, равного теплоотводу при νуст.
Задаваясь значением νуст = νдд. можно определить величину длительно допустимого тока Iдд
.
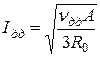Эта величина Iдд указывается в справочных данных для каждой марки и сечения жил кабеля, для различных условий прокладки (в земле, в воздухе). Итак, длительно допустимый ток – это такая величина тока в кабеле, при которой его установившаяся температура перегрева равна νдд, а срок службы его изоляции равен нормативному (20 лет).
Представим себе, что каким-либо способом получен график температуры перегрева ν(t) для заданного графика тока I(t). На этом графике максимальное значение νmax может не совпадает по времени с максимальным значением тока. Максимальный ток протекает короткое время и не вызывает из-за инерционности процесса нагрева максимального перегрева. Подставив значение νуст = νmax в выражение для установившегося перегрева найдем расчетный ток Iр:
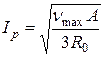. (3.5)
Итак, расчетный ток – это такое эквивалентное неизменное во времени значение тока, которое вызывает установившийся перегрев проводника, равный максимальному перегреву при изменчивом графике тока I(t).
В действительности получить график ν(t) сложно. Поэтому для нахождения Iр используют, так называемый, принцип максимума средней нагрузки, который заключается в том, что при оптимальном значении Θ=3Т0 максимальное значение графика IΘ(t) равно расчетной нагрузке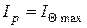 
, т.е. оптимальным для Θ является такой интервал времени, когда перегрев проводника в конце этого интервала не зависит от перегрева в начале, а целиком определяется энергией на интервале Θ.
На практике при построении суточных графиков электрической нагрузки во многих случаях принимают Θ =30 мин, что соответствует Т0 =10 минут, характерному для проводов и кабелей сечением 10...25 мм2, являющихся наиболее массовыми в сетях напряжением до 1000 В.
Порядок выполнения работы
3.3.1. Рассчитать теплоотдачу с поверхности трансформатора Т4 и кабельной линии электропередачи, используя выражение (3.3) и паспортные данные указанных элементов.
3.3.2. Для каждого интервала времени суточного графика нагрузки рассчитать температуру перегрева трансформатора Т4 и кабельной линии электропередачи на начальный и конечный моменты времени, используя выражения (3.3) и (3.4).
3.3.3. Построить на одном рисунке график токовой нагрузки кабельной линии электропередачи, питающей трансформатор Т4, графики температуры перегрева кабеля и трансформатора.
3.3.4. По графикам изменения температуры перегрева кабеля и трансформатора Т4 найти максимальные значения температуры перегрева и определить по выражению (3.5) расчетный ток для указанных элементов. Сопоставить полученные значения расчетного тока с допустимыми и сделать выводы.
3.3.5. Оформить отчет по лабораторной работе.
Контрольные вопросы
3.4.1. Что такое расчетная электрическая нагрузка?
3.4.2. Что понимается под длительно допустимой нагрузкой кабеля?
3.4.3. Чем определяется величина перегрева кабеля и трансформатора при изменяющейся нагрузке?
3.4.4. Какими факторами определяется величина максимального перегрева элемента электрической сети?
3.4.5. Чем ограничивается допустимый перегрев кабеля и трансформатора?
3.4.6. Что такое принцип максимума средней нагрузки?
3.4.7. В чем состоит сущность вероятностной модели расчетной нагрузки?
3.4.8. Назовите три вида допустимой температуры перегрева элемента электрической сети.
3.4.9. В чем заключается физический смысл постоянной времени нагрева элемента электрической сети?
3.4.10. Какие величины электрической нагрузки являются расчетными для проводников и трансформаторов?
Лабораторная работа № 4
