Министерство образования Республики Беларусь
Белорусский национальный технический университет
Кафедра “Горные машины”
Г.В. Казаченко, С.Г. Шульдова
Учебно-методическое пособие
к выполнению курсовой работы
по дисциплине «Математические модели и методы
в горном производстве»
Минск
Составители:
Г. В. Казаченко, С.Г. Шульдова
Рецензенты:
Ю. Шпургалов, Ю. И. Тарасов
В пособии приведены сведения о составе и объеме курсовой работы по дисциплине “ Математические модели и методы в горном производстве ” для студентов специальности 1-36 10 01 “Горные машины и оборудование”. Определено содержание курсовой работы и даны основные расчетные зависимости для составления балансовых соотношений по мощности и производительности мобильной горной машины. Приведены исходные данные для выполнения расчетов и их анализа.
УДК
ББК
К
Введение
Курсовая работа посвящена моделированию стационарного процесса работы горной мобильной технологической машины на основе законов сохранения и выражается в определении двух основных расчетных параметров – скорости исполнительного органа и скорости подачи. Модель рабочего процесса горной машины описывается с помощью двух основных балансовых соотношений – уравнений баланса мощности и производительности. Их составление, численное решение и анализ результатов составляет основное содержание работы. При выполнении курсовой работы студенты обязаны проанализировать схему работы одной из машин, на которой используется исполнительный орган, определенный заданием на проектирование, а также изучить устройство машины и принцип ее действия.
Формирование математической модели
Основные расчетные зависимости
Формирование математической модели движения машины при выполнении технологического процесса начинается с составления уравнений балансов мощности и производительности.
Уравнение баланса мощности в самой общей форме можно представить в виде
, кВт, (1.1)
где N – общая мощность источников энергии, работающих одновременно;
Ni – мощность, затрачиваемая на выполнение отдельной операции технологического процесса, выполняемого машиной;
n – общее число выполняемых операций (потребителей энергии).
Горные мобильные технологические машины, как правило, имеют основной рабочий орган – орган разрушения породы, а также органы передвижения и подачи, погрузки и перемещения породы и др. Привод активных рабочих органов может осуществляться от одного или нескольких двигателей. При многодвигательном приводе уравнение баланса мощности распадается на совокупность уравнений
, кВт, (1.2)
где Nj – мощность j - го двигателя;
Nk – мощность, потребляемая органами, приводимыми от j – го двигателя;
m – число органов, приводимых от j – го двигателя.
В большинстве горных машин и комбайнов общие затраты мощности состоят из
– мощности для разрушения массива полезного ископаемого;
– мощности на погрузку отбитой горной породы на конвейер или другое транспортное средство;
– мощности на подачу исполнительного органа на забой;
– мощности на передвижение машин.
Этот перечень мощностей не является исчерпывающим. В зависимости от конструкции машины некоторые из них не входят в уравнение баланса мощности, тогда как наоборот могут и входить другие составляющие. Например, мощность для разгона породы (мощность на сообщение кинетической энергии), мощность на подъем породы органом разрушения и т.п.
Второе уравнение математической модели – уравнение баланса производительности. Это уравнение записывается для органа разрушения и имеет вид
, м3/с, (1.3)
где Qx – производительность машины по ходу;
Qpo – производительность исполнительного органа по отбитой породе.
Эти производительности, как и в случае уравнения баланса мощности, зависят от конструкции машины и режимных параметров ее работы. Конкретные выражения для определения мощности и производительности приводятся при рассмотрении типовых исполнительных органов. Отдельные составляющие общих затрат мощности горной мобильной технологической машины зависят от типа и конструкции исполнительного органа, других механизмов, работающих одновременно с ним, а также режимов их работы. В настоящей курсовой работе рассматриваются упрощенные схемы горных мобильных машин, на основе которых можно сформировать уравнения балансов мощности и производительности. Расчетные зависимости даются без выводов и обоснований, с которыми студенты ознакомятся при изучении специальных дисциплин “Горные машины и оборудование”, “Проектирование горнодобывающих машин” и др. Эти формулы приводятся для наиболее широко распространенных исполнительных органов мобильных технологических машин, используемых при создании горных выработок, добыче полезных ископаемых и других горных работах.
Для всех рабочих органов основная составляющая общих затрат мощности – мощность на разрушение породы – определяется по формуле
, кВт, (1.4)
где ep – удельные затраты мощности, Вт·с/м3;
h -– к.п.д. привода исполнительного органа;
1000 – переводной коэффициент для получения результата в кВт.
Удельные затраты мощности определяются расчетным путем
, Вт·с /м3, (1.5)
где с 1 и с 2 – коэффициенты, зависящие от прочности породы, геометрии резца и других параметров, характеризующих конкретные условия разрушения породы;
h – средняя толщина стружки, снимаемая резцами органа разрушения.
Мощность для подачи исполнительного органа на забой определяется выражением
, кВт, (1.6)
где Pn – усилие подачи, Н;
Jn – скорость подачи, м/с;
η1 – к.п.д. привода механизма подачи.
Усилие подачи принимается пропорциональным силе сопротивления разрушению породы (силе резания).
, Н, (1.7)
где kn – коэффициент пропорциональности;
Pp = 1000·η· N 1/J p – сила резания, Н (1.8)
J p – скорость резания, м/с.
Мощность на передвижение машины
, кВт, (1.9)
где Рсд – сила сопротивления движению, Н;
J Т – теоретическая скорость движения, м/с;
η2 – к.п.д. привода механизма передвижения.
, Н, (1.10)
где kсд – коэффициент сопротивления движению;
m – масса машины, кг;
φ – угол наклона опорной поверхности, град;
Pz – равнодействующая сил, прижимающих машину к опорной поверхности. Например, силы тяжести, вертикальной составляющей сил сопротивления разрушению породы и др.
В тех случаях, когда сила подачи создается механизмом передвижения машины, мощности для подачи исполнительного органа и передвижения машины могут быть объединены
N 2 + N 3 = 
, кВт, (1.11)
Мощность на подъем отбитой породы органами погрузки в общем виде может быть вычислена по формуле
, кВт, (1.12)
где r - плотность породы, кг/м3;
Hn – высота подъема породы исполнительным органом, м;
h4 – к.п.д. механизма погрузки.
В ряде машин, исполнительные органы которых движутся со сравнительно большими скоростями, значительная часть мощности тратится на разгон разрушенной породы. Эта мощность обычно вычисляется по формуле
, кВт, (1.13)
где J n – скорость, сообщаемая породе исполнительным органом, м/с.
Другие составляющие затрат мощности, а также производительности исполнительных органов определяются формулами, которые приводятся при рассмотрении расчетных схем.
Расчетные схемы
Дисковая фреза
Дисковая фреза – широко применяемый орган разрушения пород, который используется в мобильных машинах для добычи кускового торфа, нарезки строительного камня, устройства дрен и коммуникационных каналов По такому же принципу работают цилиндрические фрезы, барабаны и т.п.
Расчетная схема прицепного машинно-тракторного агрегата с исполнительным органом в виде дисковой фрезы приведена на рис. 2.1.
При разработке математической модели учитываются мощности:
– на разрушение породы N 1 (по формулам 1.4 и 1.5);
– на сообщение разработанной породе кинетической энергии N 2 (формула 1.13);
– на подъем породы
, кВт (2.1)
– на перемещение агрегата
, кВт, (2.2)
где 
– угол контакта фрезы с залежью;
D – диаметр фрезы по концам резцов, м;
H – глубина разрабатываемого слоя породы, м;
– окружная сила сопротивления резанию, Н;
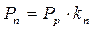–сила сопротивления подаче, Н;
kn – коэффициент пропорциональности;
– производительность по ходу, м3/с;
В – ширина захвата, м.
|
|
б)
Рисунок 2.1– Расчетная схема прицепного агрегата с исполнительным
органом в виде дисковой фрезы а) вид сбоку; б) сечение выработки
1 – резец, 2 – дисковая фреза, 3 – рама, 4 – тягач;
5 – направляющий кожух
При определении удельных затрат мощности на разрушение породы средняя толщина стружки, снимаемая резцами фрезы
, м,
где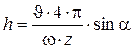 
– максимальная толщина стружки, снимаемой резцами фрезы;
w – угловая скорость вращения фрезы, рад/с;
z – число резцов на фрезе.
Приведенные зависимости для вычисления мощностей, потребляемых машиной при выполнении рабочего процесса, дают возможность сформировать уравнение баланса мощности в общем виде
, (2.3)
где kN – коэффициент запаса мощности.
Для формирования уравнения баланса производительности используем формулу, с помощью которой находится производительность такой фрезы
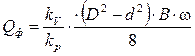, (2.4)
где kV – коэффициент заполнения рабочего пространства;
kp – коэффициент разрыхления породы исполнительным органом;
d – диаметр диска фрезы.
Так как , то легко формируется уравнение баланса производительности
, (2.5)
где kQ – коэффициент запаса производительности.
Уравнения (2.3, 2.5) могут быть использованы для решения различных задач при создании и эксплуатации мобильных технологических машин с исполнительными органами, содержащими дисковые фрезы. В настоящей работе ставится задача определить такие значения ϑ n и w, при которых соблюдается уравнение (2.5) и полностью используется мощность двигателя (2.3).
Совместное решение уравнений (2.3, 2.5) позволяет решить поставленную задачу одним из способов решения систем нелинейных уравнений при значениях исходных данных, приведенных в таблице 1 приложения.
Цепной бар
Цепной бар один из первых исполнительных органов, который применялся для механизации работ при отбойке и выемке каменного угля. В настоящее время он применяется как при выполнении открытых горных работ, так и в условиях подземных разработок. Схема машины с рабочим оборудованием в виде цепного бара представлена на рис. 2.2.
Балансовые соотношения для машины, оснащенной цепным баром, устанавливаются следующим образом. Мощность, потребляемая механизмами машины
N = N 1 + N 2 + N 3, кВт (2.6)
где N 1 – мощность на разрушение породы, определяемая по формуле (1.4).
|
|
|
Рисунок 2.2 – Расчетная схема машины с исполнительным
органом в виде цепного бара а) схема машины; б) сечение выработки
1 – цепной бар, 2 – гусеничное энергетическое мобильное средство
Толщина стружки, срезаемой резцами бара, рассчитывается по
формуле
, (2.7)
где u – скорость движения резцов, м/с;
t – шаг установки резцов, м;
– действительная скорость передвижения машины, м/с;
–коэффициент буксования;
α – угол наклона бара к горизонту, град.
Вторая составляющая затрат мощности N 2 представляет собой мощность, необходимую для подъема отбитой породы, и определяется по формуле
, (2.8)
где Hh – высота подъема горной породы баром; η1– коэффициент полезного действия бара как подъемного механизма. Остальные величины, входящие в формулу (2.8) имеют тот же смысл, что и в (1.12).
Третья составляющая N 3 вычисляется по формуле аналогичной (2.4).
, кВт, (2.9)
где η2 – к.п.д привода механизма передвижения агрегата.
Равнодействующую РР сил сопротивления можно определить по формуле
, Н. (2.10)
Представленные соотношения для определения затрат мощности позволяют сформировать для рассматриваемой машины уравнение баланса мощности.
Для составления баланса производительности приведем формулу вычисления производительности цепного бара
, м3/с, (2.11)
где hp – вылет резца, м.
Остальные величины и коэффициенты имеют смысл, описанный ранее.
Таким образом, как и для предыдущего агрегата, приведены все зависимости для составления системы уравнений, моделирующей стационарный режим работы мобильной технологической машины с рабочим органом в виде цепного бара. Исходные данные для расчетов и анализа решений приведены в таблице 2 приложения.
2.3 Шнек– фреза
Машины с таким исполнительным органом чрезвычайно широко распространены в горнодобывающей промышленности. Примером тому может служить почти исключительное ее использование в комбайнах для выполнения очистных работ при разработке угольных и калийных подземных месторождений. Такой же тип исполнительного органа применяется в машинах для разработки торфяных месторождений и профилирования поверхности дорог. Одна из возможных схем машин приведена на рис. 2.3.
|
А повернуто
Рисунок 2.3– Расчетная схема машины с исполнительным органом в виде шнек-фрезы
1 – шнек-фреза; 2 – корпус; 3 – привод
Мощность для работы подобной машины может быть представлена как сумма трех составляющих. Первая, как и в предыдущих машинах, есть мощность для разрушения породы, которая, как и для дисковой фрезы, вычисляется также по формуле (1.4). Однако, при вычислении максимальной толщины стружки вместо числа резцов z для фрез с непрерывной режущей кромкой подставляется число заходов фрезы, а для фрез с резцами, установленными на винтовой поверхности лопасти, среднее число резцов в линиях резания.
Вторая составляющая затрат мощности есть затраты на передвижение машины и подачу исполнительного органа и вычисляется по формуле
, кВт, (2.12)
где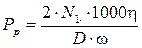 
– приведенная результирующая сил сопротивления.
Третья составляющая мощности – затраты на продвижение породы шнеком фрезы вдоль его оси. Эти затраты можно вычислить по формуле
, кВт, (2.13)
где Рос – осевое усилие, действующее на лопасть шнека, Н;
D – наружный диаметр лопасти, м;
f – коэффициент трения отбитой породы о лопасть шнека.
Осевое усилие, действующее на лопасть шнека
, Н, (2.14)
где m 2 – масса грунта, перемещаемого шнеком, кг
, кг, (2.15)
где ϑос – скорость перемещаемого грунта, м/с.
Эта скорость вычисляется по формуле
, м/с, (2.16)
где ψ – коэффициент, учитывающий циркуляцию (вращение) породы при ее перемещении шнеком;
hb – шаг шнека, м.
Таким образом, имеются все зависимости, необходимые для формирования уравнения баланса мощности. Для шнек-фрезы в стационарном режиме должны выполняться два условия достаточности производительности. Первое из которых такое же как и для дисковых фрез, а второе состоит в обеспечении производительности по перемещению породы. В этой работе используется второе условие, так как на практике его обеспечение вызывает затруднения наиболее часто. При использовании этого условия вычисляется объемная производительность шнек-фрезы по перемещаемой породе
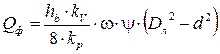, м3/с, (2.17)
где d – внутренний диаметр шнека, м.
Исходные данные для выполнения расчетов приведены в таблице 3 приложения.
Многоковшовая рама
Такого типа исполнительный орган используется в экскаваторах непрерывного действия, уборочных торфяных машинах, а также ряде других машин. Машина с многоковшовой рамой схематично представлена на рисунке 2.4.
Рисунок 2.4– Расчетная схема машины с исполнительным органом в виде ковшовой рамы
1 – корпус машины; 2 – ковшовая рама; 3 – приемно-погрузочное устройство; 4 – ковш
Мощность для работы ковшовой рамы тратится на разрушение массива, подъем породы и перемещение машины.
Как и для ранее рассмотренных исполнительных органов мощность N1 на разрушение породы рассчитывается по формуле (1.4), N2 на подъем породы – по формуле (1.12), на перемещение машины выражением
, кВт, (2.18)
Удельные затраты энергии на разрушение массива определяются по формуле (1.5), а толщина стружки, снимаемой ковшами выражением
, (2.19)
где u – скорость движения ковшей, м/с;
t – шаг установки ковшей, м;
ϑ – скорость движения машины, м/с.
Вторая составляющая N2 затрат вычисляется обычным способом, в необходимые для вычисления третьей составляющей затрат мощности приведенная равнодействующая РР сил резания и равнодействующая Pn сил сопротивления подаче выражениями
, Н; (2.20)
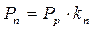, Н. (2.21)
Итак, для составления баланса мощности есть все необходимые функциональные зависимости.
Производительность машины по ходу
,м3/с (2.22)
где H – мощность вынимаемого уступа, м;
bс – толщина снимаемого слоя, м.
Производительность ковшовой рамы поперечного копания определяется выражением
,м3/с (2.22)
где Vk – объем ковша.
Таким образом, сформированы все соотношения для составления уравнений балансов мощности и производительности машины с исполнительным органом в виде ковшовой рамы поперечного копания. Анализ решений этих уравнений проводится после расчетов по исходным данным, которые приведены в таблице 4 приложения.
