Для получения ординат теоретического чертежа (ТЧ) следует обратиться к программе LS19. Однако для ее запуска недостаточно данных, содержащихся в задании – там отсутствуют длины бака и юта судна.
Для получения длин бака и юта, необходимых для запуска программы LS19, следует обратиться к программе LS28. Исходные данные, необходимые для ее запуска, и результаты расчета, полученные с помощью LS28, приведены в качестве примера в приложении Б. Никакие числовые данные брать с этого листа нельзя. Следует только отметить, что длина бака в данном случае равна длине форпика и отсчитывается она не от крайней точки носовой оконечности, а от носового перпендикуляра. Точно также длина ахтерпика отсчитывается от кормового перпендикуляра. При кормовом расположении машинного отделения длина юта равна сумме длин машинного отделения и ахтерпика. На распечатке, полученной с помощью LS28, следует вычертить в отведенном месте схему деления судна на отсеки. Высота бака и юта принимается равной 2,5 м.
Теперь можно обратиться к программе LS19. Эта программа выдает распечатку на двух листах. На первом листе приводится перечень исходных данных, а также некоторые сведения, которые потребуются при работе над теоретическим чертежом (см. приложение Б). На втором листе распечатки размещена таблица ординат ТЧ, которая не требует каких-либо комментариев. Распечатки, полученные с помощью программ LS28 и LS19, (с некоторыми пояснениями) комплектуются в отдельный раздел расчетно-пояснительной записки под именем
“2 Получение ординат теоретического чертежа”.
Расчет и построение линии седловатости ВП
На крупных судах седловатость (подъем палубы к оконечностям) может отсутствовать, но малые и средние суда строятся, как правило, с седловатостью, что улучшает их всхожесть на волну и уменьшает заливаемость палубы.
Линия седловатости – это проекция на ДП линии пересечения поверхностей палубы и борта. Ординаты линии седловатости отсчитываются от базисной линии. За базисную линию принимают прямую, проведенную параллельно ОЛ на расстоянии высоты борта от нее (рис. 2.1).
Для носовой и кормовой половин судна линия седловатости задается квадратичными параболами с нулевой ординатой на мидель-шпангоуте.
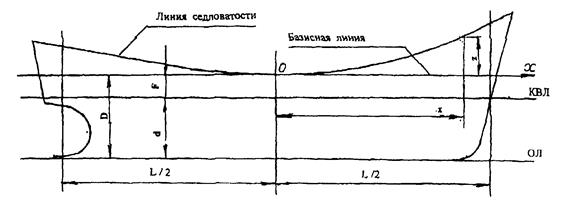
Рисунок 2.1 К построению линии седловатости
Уравнения линии седловатости имеют вид:
для носовой половины судна Zн = 0,2 (L/3 + 10) (x/L)2 ;
для кормовой половины судна Zк = 0,1 (L/3 + 10) (x/L)2.
Для упрощения предстоящих вычислений вводятся обозначения:
0,2 (L/3 + 10) = Ан ; 0,1 (L/3 + 10) = Ак .
С учетом обозначений получено:
Zн = Ан (x/L)2; Zk = Аk (x/L)2. (2.1)
Из рисунка 2.1 видно, что линия седловатости простирается за носовой и кормовой перпендикуляры. Чтобы не экстраполировать линию седловатости “на-глаз”, следует вычислить ее ординаты для минус 1-го и 21-го шпангоутов. Расчет по формулам (2.1) должен проводиться в табличной форме (табл. 2.1).
Таблица 2.1 Расчет ординат линии седловатости
| Номера шпангоутов | Относительная абсцисса x/L | (x/L)2 | Ординаты, м Z = А (x/L)2 |
| -1 | 0,55 | 0,3025 | |
| 0,50 | 0,2500 | ||
| 0,45 | 0,2025 | ||
| 0,40 | 0,1600 | ||
| 0,35 | 0,1225 | ||
| 0,30 | 0,0900 | ||
| 0,25 | 0,0625 | ||
| 0,20 | 0,0400 | ||
| 0,15 | 0,0225 | ||
| 0,10 | 0,0100 | ||
| 0,05 | 0,0025 | ||
| -0,05 | 0,0025 | ||
| -0,10 | 0,0100 | ||
| -0,15 | 0,0225 | ||
| -0,20 | 0,0400 |
Продолжение таблицы 2.1
| -0,25 | 0,0625 | ||
| -0,30 | 0,0900 | ||
| -0,35 | 0,1225 | ||
| -0,40 | 0,1600 | ||
| -0,45 | 0,2025 | ||
| -0,50 | 0,2500 | ||
| -0,55 | 0,3025 |
Результаты расчета отображаются на рисунке (рис. 2.2). При построении линии седловатости масштаб по длине принимается произвольный, а по высоте – обязательно 1: 100. На оси абсцисс отмечаются номера теоретических шпангоутов.

Рисунок 2.2 Линия седловатости






