МАТЕМАТИКА
в формулах и таблицах
Справочное пособие
Новосибирск
2000 г.
В.И.Агульник, Б.П.Зеленцов.
Математика в формулах и таблицах. Справочное пособие
Справочное пособие содержит формулы, таблицы, графики по математике, охватывающие основные разделы элементарной математики - алгебры и геометрии. Оно предназначено для абитуриентов при подготовке к вступительным экзаменам, а также для студентов дневного и заочного обучения при изучении высшей математики и других дисциплин.
Кафедра высшей математики
Рецензент: И.И.Резван
Утверждено редакционно-издательским советом СибГУТИ в качестве учебного пособия.
Ó Сибирский государственный университет телекоммуникаций и информатики, 2000 г.
Ó В.И.Агульник, Б.П.Зеленцов, 2000 г.
ОГЛАВЛЕНИЕ
1. ЧИСЛА, ДРОБИ, МОДУЛИ…………………………………
2. ФОРМУЛЫ СОКРАЩЕННОГО УМНОЖЕНИЯ …………
3. СТЕПЕНИ И КОРНИ ……………………………………….
4. КВАДРАТНЫЕ УРАВНЕНИЯ И НЕРАВЕНСТВА ………
5. ПРОГРЕССИИ ………………………………………………
6. ЛОГАРИФМЫ ………………………………………………
7. ТРИГОНОМЕТРИЯ ………………………………………
8. ОСНОВНЫЕ ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ ……………
9. ПЛАНИМЕТРИЯ …………………………………………
10. СТЕРЕОМЕТРИЯ …………………………………………
ЛИТЕРАТУРА …………………………………………………
ЧИСЛА, ДРОБИ, МОДУЛИ
n Î N - множество натуральных чисел 
{1, 2, 3, …}
d = НОД (n, m) - наибольший общий делитель n и m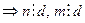 
k = НОК (n, m) - наименьшее общее кратное n и m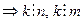 
Z =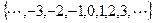 
множество целых чисел
Q =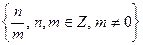 
- множество рациональных чисел (дробей)
R – множество действительных чисел
Арифметические операции с дробями:
; 
; 
;
; 
; 
;
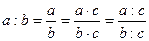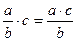Пропорция 
;
Модуль числа. Определение: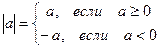 
;
Свойства модуля:
; 
; 
;
|
|
|
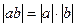
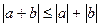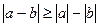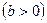; x
;
|
|
|
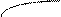
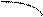
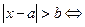
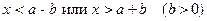ФОРМУЛЫ СОКРАЩЕННОГО УМНОЖЕНИЯ
; 
;
;
;
;
; 
;
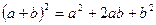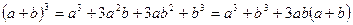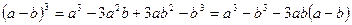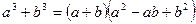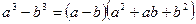СТЕПЕНИ И КОРНИ
; 
; 
; 
;
; 
; 
; 
;
; 
; 
;
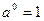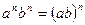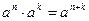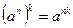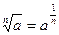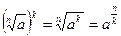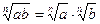КВАДРАТНЫЕ УРАВНЕНИЯ
; 
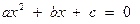Корни уравнения: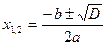 
, где 
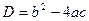- дискриминант.
Формулы Виета: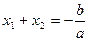 
; 
.
Разложение квадратного трехчлена на множители:
.
Приведенное уравнение: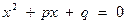 
; 
.
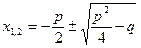Квадратное неравенство:
Если D >0, a >0,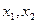 
- корни квадратного трехчлена, 
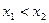, то
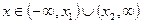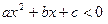Þ 
;
Þ 
.
ПРОГРЕССИИ
Арифметическая прогрессия: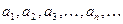 
Общий член: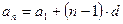 
, 
, где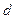 
- разность прогрессии;
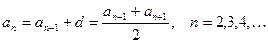
Сумма членов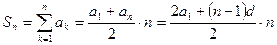 
.
Геометрическая прогрессия 
Общий член: 
, где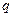 
- знаменатель прогрессии;
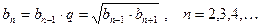
Сумма членов 
.
Сумма геометрической прогрессии (при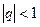 
): 
.
Некоторые суммы:
; 
;
;
; 
;
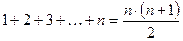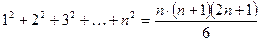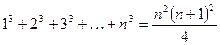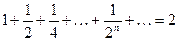ЛОГАРИФМЫ
Логарифм числа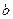 
по основанию 
:
.
Основное логарифмическое тождество: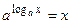 
.
Свойства логарифмов:
; 
;
; 
; 
.
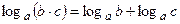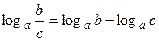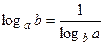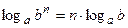Десятичные логарифмы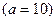 
: 
.
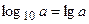Натуральные логарифмы 
: 
.
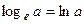Логарифмические неравенства:
.
Показательные неравенства:
.
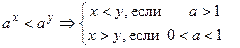ТРИГОНОМЕТРИЯ
Основные соотношения
;
; 
;
; 
; 
;
; 
;
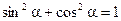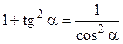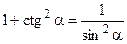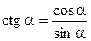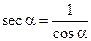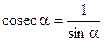7.2. Перевод из радианной меры углов в градусную и обратно:
; 
;
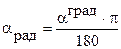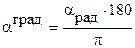Основные значения тригонометрических функций
| 
| 
| 
| 
| 
| 
| 
| |
| 
| 
| 
| 
| 
|
| 
|
|
|
|
|
|
|
|
|
|
|
|
| 
|
| 
| 
|
|
|
|
|
|
|
|
|
|
|
|
|
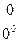
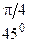
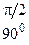
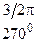
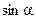
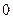
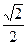
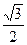
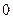
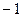
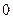
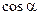
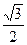
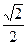
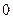
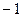
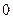
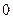
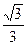
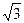
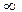
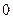
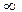
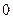
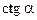
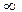
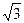
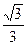
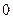
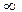
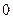
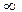
Знаки тригонометрических функций
 |  | |
Формулы сложения
; 
;
; 
;
; 
;
; 
;
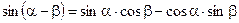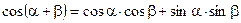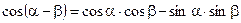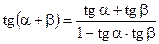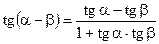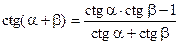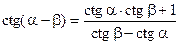Формулы двойных углов
;
;
; 
;
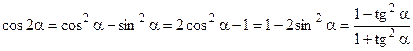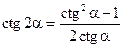Формулы тройных углов
; 
;
; 
;
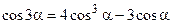Формулы половинных углов
; 
;
; 
;
;
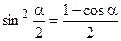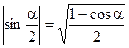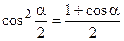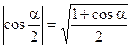Универсальная тригонометрическая подстановка, используемая для решения тригонометрических уравнений:
; 
; 
; 
;
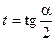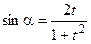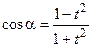Формулы приведения
| 
| 
| 
| 
| |
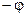
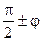
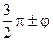
| sin | – sin j | cos j | ± sin j | – cos j | ± sin j |
| cos | cos j | ± sin j | – cos j | ± sin j | cos j |
| tg | –tg j | ± ctg j | ± tg j | ± ctg j | ± tg j |
| ctg | –ctg j | ± tg j | ± ctg j | ± tg j | ± ctg j |
Формулы преобразования суммы и разности
; 
;
; 
;
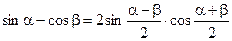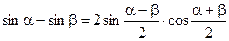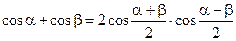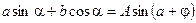, где 
;
; 
;
; 
.
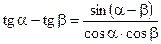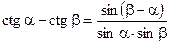