Законы распределения: биноминальный, Пуассона
1. Дан закон распределения ДСВ Х:
| хi | -1 | ||
| рi | 0,2 | р | 0,3 |
Найти: а) вероятность р; б) Р (Х 
0); в) Р(-1<X<3); г) P(-2 X<0); д) P(X>-1); е) функцию распределения F(x). Построить график функции распределения и полигон. Вычислить М [Х] и D[Х].
2. Дан закон распределения ДСВ Х:
| хi | ||||
| рi | 0,2 | 0,1 | 0,4 | 0,3 |
Найти: а) Р (Х>2); б) Р(1,5 
3,5); в) Р (Х<4); г) Р(2 Х<5); д) функцию распределения; е) M[Х]; ж) D[Х]. Построить график функции распределения и полигон.
3. Дан закон распределения ДСВ Х:
| хi | |||
| рi | р1 | р2 | ¼ |
Найти р1 и р2, если М [Х]=1. Найти: а) P(-1<X<3); б) P(0<X 3);
в) P(2 X<4); г) D[Х]. Построить график функции распределения.
4. Выполнить задания предыдущей задачи, если закон распределения задан таблицей:
| хi | |||
| рi | р1 | р2 | 1/4 |
и М [Х]=7/4.
5. Найти: а) закон распределения; б)М[Х]; в) D [Х]; г) P (1<X<2);
д) Р(X 1,5), если функция распределения случайной величины Х равна
0, если х 0,
3/5, если 0<x 1,
F (x) = 4/5, если 1<x 1,5
14/15, если 1,5<x 3,
1, если х>3
6. Студент знает 10 из 15 экзаменационных вопросов. Ему задают два вопроса, случайным образом выбранные из списка. Случайная величина Х – число вопросов, на которые ответил студент. Найти закон распределения данной случайной величины, М [Х], D[Х].
7. В лотерее на каждые 100 билетов один выигрывает 500 рублей, два – по 300 рублей, три – по 100. Построить закон и функцию распределения выигрыша владельца одного билета, если билет стоит 50 рублей. Найти математическое ожидание выигрыша.
8. Два стрелка независимо друг от друга делают по одному выстрелу в мишень. Вероятность попадания в мишень для первого стрелка – 0,7, для второго стрелка – 0,8. Случайная величина Х – суммарное число попаданий в мишень в данном эксперименте. Найти закон распределения данной случайной величины, M[Х], D[Х].
9. Бросают четыре монеты. Найти: а) закон и функцию распределения числа выпавших гербов; б) математическое ожидание и дисперсию этой случайной величины.
10. В среднем около 20% клиентов, обратившихся в фирму «Турсервис», оказываются недовольными уровнем обслуживания в этой фирме. Найти: а) закон и функцию распределения числа недовольных среди трех случайным образом выбранных клиентов; б) математическое ожидание и дисперсию этой случайной величины.
11. Три читателя библиотеки взяли по экземпляру одной и той же книги. Раскрыв наугад книгу, они ищут на этой странице опечатку. Вероятность найти опечатку на одной странице равна 0,05. Найти математическое ожидание и дисперсию числа обнаруженных страниц с опечатками и вероятность того, что это число не больше 1.
12. Из урны, содержащей 2 белых и 3 черных шара, вынимается шар, записывается его цвет и шар возвращается обратно. Опыт повторяется 5 раз. Найти математическое ожидание и дисперсию числа появлений белого шара, а также вероятность того, что это число будет не меньше 2.
13. Цех, выпускающий электробритвы, дает в среднем 10% брака. Найти математическое ожидание и дисперсию количества бракованных экземпляров среди 30 наугад выбранных бритв.
14. В условиях задачи 3.5.20 найти: а) математическое ожидание числа страховок, выплаченных компанией за год; б) среднюю годовую прибыль страховой компании.
15. Среднее число вызовов, поступающих на АТС в минуту, равно 120. Найти вероятность того, что: а) за две секунды на АТС поступит менее 2 вызовов; б) за одну секунду на АТС поступит ровно три вызова; в) за три секунды на АТС поступит не менее трех вызовов.
16. В тесто кладется изюм из расчета три изюминки на булку. Найти вероятность того, что в купленной булке: а) нет ни одной изюминки; б) больше трех изюминок; в) ровно четыре изюминки. Сколько изюма надо класть в тесто, чтобы вероятность иметь хотя бы одну изюминку в булке была не меньше 0,99?
17. Корректура в 500 страниц содержит 1300 опечаток. Найти наиболее вероятное число опечаток на одной странице текста и вероятность этого числа.
18. Устройство состоит из большого числа независимо работающих элементов с одинаковой (очень малой) вероятностью отказа каждого элемента за время Т. Найти среднее число отказавших за время Т элементов, если вероятность того, что за это время откажет хотя бы один элемент, равна 0,95.
19. За час в базу данных поступает в среднем 120 запросов. Найти вероятность следующего события A: за данную минуту поступит четыре запрос.
20. Данный наборщих в среднем делает одну ошибку на две страницы текста. В набранной книге взяли наугад страницу. Найти вероятности следующих событий: A – на странице нет опечаток; B – на странице больше одной опечатки.
21. В тесто положили изюм из расчета по пять изюмин на одну булку и хорошо перемешали тесто. Взяли наугад булку. Найти вероятность следующего события A: во взятой наугад одной булке есть хотя бы одна изюмина.
22. Монета подбрасывается 5 раз, X – дискретная случайная величина, равная разности между числом выпавших орлов и числом выпавших решек. Для случайной величины X найти математическое ожидание M(X).
23. На связке пять разных ключей, ровно один из которых подходит к замку. Некто по очереди вставляет ключи в замок до тех пор, пока не откроет дверь (не подошедшие ключи откладываются в сторону). Пусть X – дискретная случайная величина, равная числу попыток. Для случайной величины X найти математическое ожидание M(X).
24. Среди десяти шаров имеется три черных. Наудачу выбрано два шара. Пусть X – дискретная случайная величина, равная числу черных шаров среди двух выбраных. Для случайной величины X найти математическое ожидание M(X).
25. Вероятность попадания в цель при одном выстреле равна p. Стреляют до первого попадания в цель. Пусть X – дискретная случайная величина, равная числу произведенных выстрелов. Для случайной величины X найти математическое ожидание M(X).
4.3.2. Плотность распределения, функция распределения и числовые характеристики непрерывной случайной величины (НВС).
Нормальное распределение
1. Плотность распределения вероятностей НСВ Х имеет вид:
Сх2, если - 1 х 1,
f (x)=
0, если |x|>1.
Найти: а) константу С; б) Р (Х 
[-2;0]); в) M[Х]; г) D[Х]; д) функцию распределения F(x).
2. Плотность распределения вероятностей НСВ Х имеет вид:
0, если х 
[0; 
],
f (x)=
Csin x, если х [0; ].
Найти: а) константу С; б) Р (Х [ /3; 5 /4]); в) M[Х]; г) функцию распределения F(x).
3. Плотность распределения вероятностей НСВ Х имеет вид:
0, если x<5,
f (x)=
C/x5, если х 
5.
Найти: а) константу С; б) M[Х]; в) D[Х]; г) P(2<Х<10); д) функцию распределения F(x).
4. Плотность распределения вероятностей НСВ Х имеет вид:
0, если x<1,
f (x)=
C e-2x, если х 1.
Найти: а) константу С; б) P (|X| 2); в) функцию распределения F(x).
5. Функция распределения НСВ Х имеет вид:
1) 
0, если x<2,
F (x)= (x – 2)2, если 2 х 3
1, если x>3
2) 
Найти: а) P (0,5 X 2,5); б) M[X]; в) D[X].
Законы распределения и числовые характеристики случайных векторов.
6. Дан закон распределения случайного вектора (X,V) дискретного типа:
| yj xi | |||
| - 1 | 0,1 | 0,05 | 0,05 |
| 0,35 | 0,25 | 0,2 |
а) Найти: Р (Х= -1, Y=1), P(X=1, Y>0), P(X Y), P(XY 0).
б) Найти безусловные законы распределения каждой из компонент случайного вектора (X,Y).
в) Выяснить, зависимы или нет случайные величины X и Y.
г) Построить условный закон распределения случайной величины Y при условии Х=1 и найти условное математическое ожидание M[Y/X=1].
д) Найти математическое ожидание случайного вектора (mx, my), дисперсии DX, DY каждой компоненты, ковариацию KXY и коэффициент корреляции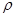 
XY.
7. Дан закон распределения случайного вектора (X,Y):
| yj xi | ||
| -1 | 0,3 | 0,12 |
| p | 0,05 | |
| 0,35 | 0,03 |
Найти: р, Р (Х=0, Y=0), P(X 
Y), P(X 0, Y=1).
Выполнить задания б) – д) из предыдущей задачи для данного случайного вектора.
Дважды бросается игральная кость. Случайные величины: X – количество выпадений нечетного числа очков, Y – количество выпадений единицы. Построить закон распределения случайного вектора (X,Y). Найти Р(X Y). Выполнить задания б) – д) из задачи4.8.1.
9. Один раз подбрасывается игральная кость. Случайные величины: Х – индикатор четного числа выпавших очков (Х=1, если выпало четное число, и Х=0 в остальных случаях), Y – индикатор числа очков, кратного трем (Y=1, если выпало число, кратное трем, и Y=0 в противном случае). Построить закон распределения случайного вектора (X,Y) и безусловные законы распределения компонент. Зависимы или нет случайные величины Х и Y? Вычислить mX, mY, DX, D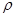Y, XY.
10. Производится два выстрела по мишени в неизменных условиях. Вероятность попадания в мишень при одном выстреле равна 0,6. Случайные величины: Х – число промахов, Y – индикатор попадания при первом выстреле (Y=1, если при первом выстреле было попадание в мишень, и Y=0 в остальных случаях). Построить закон распределения случайного вектора (X,Y) и безусловные законы распределения компонент. Вычислить mX, mY, DX, DY, 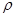XY. Зависимы или нет случайные величины Х и Y?
11. Производится два независимых выстрела по цели с вероятностью попадания в цель, равной 0,6 при первом выстреле и 0,8 при втором. Случайные величины: Х – число попаданий при первом выстреле, Y – число попаданий при втором выстреле. Построить закон распределения случайного вектора (X,Y).
12. Из колоды в 36 карт наугад достают одну карту. Случайные величины: а) Х – число вынутых тузов, Y – число вынутых крестовых карт;
б) Х – число вынутых тузов, Y – число вынутых карт-картинок. Построить закон распределения случайного вектора (X,Y). Найти коэффициент корреляции 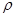XY. Выяснить, зависимы Х и Y или нет.
