Частному решению линейного неоднородного дифференциального 
по виду его правой части соответствует функция …
| 
| ||
| |||
| |||
|
Тема: Дифференциальные уравнения высших порядков
Общее решение дифференциального уравнения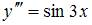 
имеет вид …
|
| 
| ||
| |||
| |||
|
Тема: Дифференциальные уравнения первого порядка
Дано дифференциальное уравнение 
при 
. Тогда интегральная кривая, которая определяет решение этого уравнения, имеет вид …
|
| C | ||
| B | |||
| A | |||
| D |
Тема: Кривые второго порядка
Если уравнение окружности имеет вид 
, то его центром C и радиусом r являются …
|
|  , 
| ||
 ,
| |||
, 
| |||
| ,
|
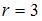
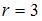
Тема: Основные задачи аналитической геометрии в пространстве
В пространстве имеется отрезок, соединяющий две точки с ординатами одинаковых знаков. Тогда этот отрезок не может пересекать …
|
| плоскость Oxz | ||
| плоскость Oxy | |||
| плоскость Oyz | |||
| ось ординат |
Тема: Вычисление определителей
Определитель 
равен …
|
| – 30 | ||
| – 15 |
Тема: Умножение матриц
Дана матрица 
. Тогда матрица 
имеет вид …
|
| 
| ||
| |||
| |||
|
Тема: Скалярное произведение векторов
Если 
, 
и 
, тогда угол между векторами 
и 
равен …
|
| 
| ||
| |||
| |||
|
Тема: Прямая на плоскости
Уравнением прямой, перпендикулярной прямой 
, является …
|
| 
| ||
| |||
| |||
|
Тема: Системы линейных уравнений: основные понятия
Установите соответствие между системой линейных уравнений и ее расширенной матрицей.
1. 
2. 
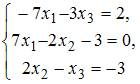
3. 
4. 
| |||
| |||
| |||
| |||
| |||
|
Тема: Линейные операции над векторами
Упрощение выражения 
приводит его к виду …
|
| 
| ||
| |||
| |||
|
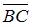
Тема: Линейные дифференциальные уравнения 2 порядка
Дано линейное однородное дифференциальное уравнение 
, тогда его общее решение имеет вид …
|
| 
| ||
| |||
| |||
|
Тема: Дифференциальные уравнения высших порядков
Общее решение дифференциального уравнения 
имеет вид …
|
| 
| ||
| |||
| |||
|
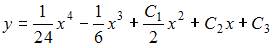
Тема: Дифференциальные уравнения первого порядка
Общий интеграл дифференциального уравнения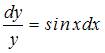 
имеет вид …
|
| 
| ||
| |||
| |||
|
Тема: Типы дифференциальных уравнений
Из данных дифференциальных уравнений уравнениями c разделяющимися переменными являются …
|
| 
| ||
|
| 
| ||
| |||
|
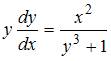
Тема: Интерполирование функций: интерполяционный многочлен Лагранжа
График функции 
проходит через точки
Тогда ее интерполяционный многочлен второго порядка равен …
|
| 
| ||
| |||
| |||
|
Тема: Численное дифференцирование и интегрирование
Значение функции 
в точке 
можно вычислить по формуле …
|
| 
| ||
| |||
| |||
|
Тема: Численные методы анализа
Действительный корень уравнения 
принадлежит интервалу …
|
| 
| ||
| |||
| |||
|
Тема: Численные методы решения алгебраических уравнений
Три итерации метода половинного деления при решении уравнения 
на отрезке 
требуют последовательного вычисления значений функции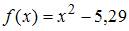 
в точках …
|
| 
| ||
| |||
| |||
|
Тема: Мера плоского множества
Мера множества, изображенного на рисунке,
равна …
|
| 
| ||
| |||
| |||
|
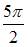
