V3: {{35}} 04.03.31. Замена переменной в неопределенном интеграле
I:{{353}} ТЗ-21; t=0; k=4; ek=0; m=0; c=0;
S: В неопределенном интеграле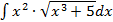 
введена новая переменная 
. Тогда интеграл примет вид:
+: 
-: 
-: 
-: 
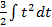
I:{{354}} ТЗ-22; t=0; k=4; ek=0; m=0; c=0;
S: В неопределенном интеграле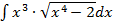 
введена новая переменная 
. Тогда интеграл примет вид:
+: 
-: 
-: 
-: 
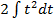
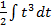
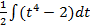
I:{{355}} ТЗ-23; t=0; k=4; ek=0; m=0; c=0;
S: В неопределенном интеграле 
введена новая переменная 
. Тогда интеграл примет вид:
+: 
-: 
-: 
-:
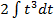
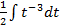
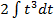
I:{{356}} ТЗ-24; t=0; k=4; ek=0; m=0; c=0;
S: В неопределенном интеграле 
введена новая переменная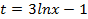 
. Тогда интеграл примет вид:
+: 
-: 
-: 
-: 
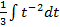
I:{{357}} ТЗ-25; t=0; k=4; ek=0; m=0; c=0;
S: В неопределенном интеграле 
введена новая переменная 
. Тогда интеграл примет вид:
+: 
-: 
-: 
-: 
I:{{358}} ТЗ-26; t=0; k=4; ek=0; m=0; c=0;
S: В неопределенном интеграле 
введена новая переменная 
. Тогда интеграл примет вид:
+: 
-: 
-: 
-: 
I:{{359}} ТЗ-27; t=0; k=4; ek=0; m=0; c=0;
S: В неопределенном интеграле 
введена новая переменная 
. Тогда интеграл примет вид:
+: 
-: 
-: 
-: 
I:{{360}} ТЗ-28; t=0; k=5; ek=0; m=0; c=0;
S: В неопределенном интеграле 
введена новая переменная 
. Тогда интеграл примет вид:
+: 
-: 
-:
-: 
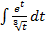
I:{{361}} ТЗ-29; t=0; k=5; ek=0; m=0; c=0;
S: В неопределенном интеграле 
введена новая переменная 
. Тогда интеграл примет вид:
+: 
-: 
-: 
-: 
I:{{362}} ТЗ-30; t=0; k=5; ek=0; m=0; c=0;
S: В неопределенном интеграле 
введена новая переменная . Тогда интеграл примет вид:
+: 
-: 
-: 
-: 
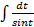
V3: {{36}} 04.03.32. Интегрирование по частям в неопределенном интеграле
I:{{363}} ТЗ-31; t=0; k=4; ek=0; m=0; c=0;
S: Множество первообразных функции 
равно
+: 
-: 
-: 
-: 
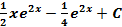
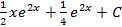
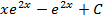
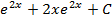
I:{{364}} ТЗ-32; t=0; k=4; ek=0; m=0; c=0;
S: Множество первообразных функции 
равно
+: 
-: 
-: 
-: 
I:{{365}} ТЗ-33; t=0; k=4; ek=0; m=0; c=0;
S: Множество первообразных функции 
равно
+: 
-: 
-: 
-: 
I:{{366}} ТЗ-34; t=0; k=3; ek=0; m=0; c=0;
S: Если в неопределенном интеграле 
, применяя формулу интегрирования по частям: 
, положить, что 
, то функция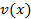 
будет равна
+: 
-: 
-: 
-: 
I:{{367}} ТЗ-35; t=0; k=3; ek=0; m=0; c=0;
S: Если в неопределенном интеграле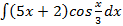 
, применяя формулу интегрирования по частям: , положить, что 
, то функция 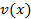будет равна
+: 
-: 
-: 
-: 
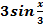
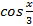
I:{{368}} ТЗ-36; t=0; k=3; ek=0; m=0; c=0;
S: Если в неопределенном интеграле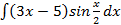 
, применяя формулу интегрирования по частям: , положить, что 
, то функция 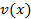будет равна
+: 
-: 
-: 
-: 
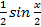
I:{{369}} ТЗ-37; t=0; k=3; ek=0; m=0; c=0;
S: Если в неопределенном интеграле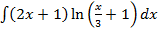 
, применяя формулу интегрирования по частям: , положить, что 
, то функция 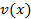будет равна
+: 
-: 
-: 
-: 
I:{{370}} ТЗ-38; t=0; k=3; ek=0; m=0; c=0;
S: Если в неопределенном интеграле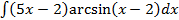 
, применяя формулу интегрирования по частям: , положить, что 
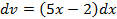, то дифференциал функции 
будет равен
+: 
-: 
-: 
-: 
I:{{371}} ТЗ-39; t=0; k=3; ek=0; m=0; c=0;
S: Если в неопределенном интеграле 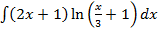, применяя формулу интегрирования по частям: , положить, что 
, то дифференциал функции будет равен
+: 
-: 
-: 
-: 
I:{{372}} ТЗ-40; t=0; k=3; ek=0; m=0; c=0;
S: Если в неопределенном интеграле 
, применяя формулу интегрирования по частям: , положить, что 
, то дифференциал функции будет равен
+: 
-: 
-: 
-: 
V3: {{37}} 04.03.33. Интегрирование рациональных дробей
I:{{373}} ТЗ-41; t=0; k=4; ek=0; m=0; c=0;
S: В неопределенном интеграле 
подынтегральная функция разлагается на элементарные дроби
+: 
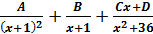
-: s w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:lang w:val="EN-US"/></w:rPr><m:t>x</m:t></m:r><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/></w:rPr><m:t>+1</m:t></m:r></m:den></m:f></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>"> 
-: 
-: 
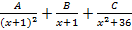
I:{{374}} ТЗ-42; t=0; k=4; ek=0; m=0; c=0;
S: В неопределенном интеграле 
подынтегральная функция разлагается на элементарные дроби
+: 
-: 
-: 
-: 
I:{{375}} ТЗ-43; t=0; k=4; ek=0; m=0; c=0;
S: В неопределенном интеграле 
подынтегральная функция разлагается на элементарные дроби
+: 
-: 
-: 
-: 
I:{{376}} ТЗ-44; t=0; k=4; ek=0; m=0; c=0;
S: В неопределенном интеграле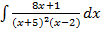 
подынтегральная функция разлагается на элементарные дроби
+: 
-: 
-: 
-: 
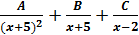
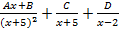
I:{{377}} ТЗ-45; t=0; k=5; ek=0; m=0; c=0;
S: Установите соответствие между неопределенными интегралами и разложением подынтегральных функций на элементарные дроби
L1: 
L2: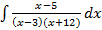 
L3: 
L4: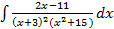 
R1: 
R2: 
R3: 
R4: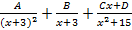 
I:{{378}} ТЗ-46; t=0; k=5; ek=0; m=0; c=0;
S: Установите соответствие между неопределенными интегралами и разложением подынтегральных функций на элементарные дроби
L1: 
L2: 
L3: 
L4: 
R1: 
R2: 
R3: 
R4: 
I:{{379}} ТЗ-47; t=0; k=5; ek=0; m=0; c=0;
S: Установите соответствие между неопределенными интегралами и разложением подынтегральных функций на элементарные дроби
L1: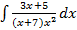 
L2: 
L3: 
L4: 
R1: 
R2: 
R3: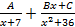 
R4: 
I:{{380}} ТЗ-48; t=0; k=5; ek=0; m=0; c=0;
S: Установите соответствие между неопределенными интегралами и разложением подынтегральных функций на элементарные дроби
L1: 
L2: 
L3: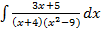 
L4: 
R1: 
R2: 
R3: 
R4: 
R5: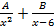 
I:{{381}} ТЗ-49; t=0; k=5; ek=0; m=0; c=0;
S: Установите соответствие между неопределенными интегралами и разложением подынтегральных функций на элементарные дроби
L1: 
L2: 
L3: 
L4: 
R1: 
R2: 
R3: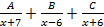 
R4: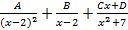 
I:{{382}} ТЗ-50; t=0; k=5; ek=0; m=0; c=0;
S: Установите соответствие между неопределенными интегралами и разложением подынтегральных функций на элементарные дроби
L1: 
L2: 
L3: 
L4: 
R1: 
R2: 
R3: 
R4: 
