бесконечно малыми.
Определение. Предел функции f(x) при х®а, где а- число, равен бесконечности, если для любого числа М>0 существует такое число D>0, что неравенство
ïf(x)ï>M
выполняется при всех х, удовлетворяющих условию
0 < ïx - aï < D
Записывается  .
.
Собственно, если в приведенном выше определении заменить условие ïf(x)ï>M на f(x)>M, то получим:

а если заменить на f(x)<M, то:

Графически приведенные выше случаи можно проиллюстрировать следующим образом:
 |
a x a x a x
Определение. Функция называется бесконечно большой при х®а, где а – чосли или одна из величин ¥, +¥ или -¥, если  , где А – число или одна из величин ¥, +¥ или -¥.
, где А – число или одна из величин ¥, +¥ или -¥.
Связь бесконечно больших и бесконечно малых функций осуществляется в соответствии со следующей теоремой.
Теорема. Если f(x)®0 при х®а (если х®¥) и не обращается в ноль, то

5. Сравнение бесконечно малых функций.
Пусть a(х), b(х) и g(х) – бесконечно малые функции при х ® а. Будем обозначать эти функции a, b и g соответственно. Эти бесконечно малые функции можно сравнивать по быстроте их убывания, т.е. по быстроте их стремления к нулю.
Например, функция f(x) = x10 стремится к нулю быстрее, чем функция f(x) = x.
Определение. Если  , то функция a называется бесконечно малой более высокого порядка, чем функция b.
, то функция a называется бесконечно малой более высокого порядка, чем функция b.
Определение. Если  , то a и b называются бесконечно малыми одного порядка.
, то a и b называются бесконечно малыми одного порядка.
Определение. Если  то функции a и b называются эквивалентными бесконечно малыми. Записывают a ~ b.
то функции a и b называются эквивалентными бесконечно малыми. Записывают a ~ b.
Пример. Сравним бесконечно малые при х®0 функции f(x) = x10 и f(x) = x.

т.е. функция f(x) = x10 – бесконечно малая более высокого порядка, чем f(x) = x.
Определение. Бесконечно малая функция a называется бесконечно малой порядка k относительно бесконечно малой функции b, если предел  конечен и отличен от нуля.
конечен и отличен от нуля.
Однако следует отметить, что не все бесконечно малые функции можно сравнивать между собой. Например, если отношение  не имеет предела, то функции несравнимы.
не имеет предела, то функции несравнимы.
Пример. Если  , то при х®0
, то при х®0  , т.е. функция a - бесконечно малая порядка 2 относительно функции b.
, т.е. функция a - бесконечно малая порядка 2 относительно функции b.
Пример. Если  , то при х®0
, то при х®0  не существует, т.е. функция a и b несравнимы.
не существует, т.е. функция a и b несравнимы.
6. Свойства эквивалентных бесконечно малых.
1) a ~ a, 
2) Если a ~ b и b ~ g, то a ~ g, 
3) Если a ~ b, то b ~ a, 
4) Если a ~ a1 и b ~ b1 и  , то и
, то и  или
или  .
.
Следствие: а) если a ~ a1 и  , то и
, то и 
б) если b ~ b1 и  , то
, то 
Свойство 4 особенно важно на практике, т.к. оно фактически означает, что предел отношения бесконечно малых не меняется при замене их на эквивалентные бесконечно малые. Этот факт дает возможность при нахождении пределов заменять бесконечно малые на эквивалентные им функции, что может сильно упростить вычисление пределов.
Пример. Найти предел 
Так как tg5x ~ 5x и sin7x ~ 7x при х ® 0, то, заменив функции эквивалентными бесконечно малыми, получим:

Пример. Найти предел  .
.
Так как 1 – cosx =  при х®0, то
при х®0, то  .
.
Пример. Найти предел 
Если a и b - бесконечно малые при х®а, причем b - бесконечно малая более высокого порядка, чем a, то g = a + b - бесконечно малая, эквивалентная a. Это можно доказать следующим равенством  .
.
Тогда говорят, что a - главная часть бесконечно малой функции g.
Пример. Функция х2 +х – бесконечно малая при х®0, х – главная часть этой функции. Чтобы показать это, запишем a = х2, b = х, тогда
 .
.
7. Некоторые замечательные пределы.

Первый замечательный предел. 

Второй замечательный предел. 
Часто если непосредственное нахождение предела какой – либо функции представляется сложным, то можно путем преобразования функции свести задачу к нахождению замечательных пределов.
Кроме трех, изложенных выше, пределов можно записать следующие полезные на практике соотношения:


Пример. Найти предел.

Пример. Найти предел.

Пример. Найти предел.

Пример. Найти предел.

Пример. Найти предел.

Пример. Найти предел  .
.
Для нахождения этого предела разложим на множители числитель и знаменатель данной дроби.
x2 – 6x + 8 = 0; x2 – 8x + 12 = 0;
D = 36 – 32 = 4; D = 64 – 48 = 16;
x1 = (6 + 2)/2 = 4; x1 = (8 + 4)/2 = 6;
x2 = (6 – 2)/2 = 2; x2 = (8 – 4)/2 = 2;
Тогда 
Пример. Найти предел.
 домножим числитель и знаменатель дроби на сопряженное выражение:
домножим числитель и знаменатель дроби на сопряженное выражение:  =
=
=  .
.
Пример. Найти предел.

Пример. Найти предел  .
.
Разложим числитель и знаменатель на множители.
x2 – 3x + 2 = (x – 1)(x – 2)
x3 – 6x2 + 11x – 6 = (x – 1)(x – 2)(x – 3), т.к.
 x3 – 6x2 + 11x – 6 x - 1
x3 – 6x2 + 11x – 6 x - 1
x3 – x2 x2 – 5x + 6
- 5x2 + 11x
- 5x2 + 5x
6x - 6
6x - 6 0
x2 – 5x + 6 = (x – 2)(x – 3)
Тогда 
Пример. Найти предел.

Для самостоятельного решения:
1) 
2) 
3) 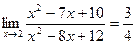
4) 
5) 
6) 
7) 
8) 
Лекция 3.
1. Непрерывность функции в точке.
Определение. Функция f(x), определенная в окрестности некоторой точки х0, называется непрерывной в точке х0, если предел функции и ее значение в этой точке равны, т.е.

Тот же факт можно записать иначе: 
Определение. Если функция f(x) определена в некоторой окрестности точки х0, но не является непрерывной в самой точке х0, то она называется разрывной функцией, а точка х0 – точкой разрыва.
Пример непрерывной функции:
y
f(x0)+e
 f(x0)
f(x0)
f(x0)-e
0 x0-D x0 x0+D x
 Пример разрывной функции:
Пример разрывной функции:
y
f(x0)+e
f(x0)
f(x0)-e
x0 x
Определение. Функция f(x) называется непрерывной в точке х0, если для любого положительного числа e>0 существует такое число D>0, что для любых х, удовлетворяющих условию

верно неравенство  .
.
Определение. Функция f(x) называется непрерывной в точке х = х0, если приращение функции в точке х0 является бесконечно малой величиной.
f(x) = f(x0) + a(x)
где a(х) – бесконечно малая при х®х0.
2. Свойства непрерывных функций.
1) Сумма, разность и произведение непрерывных в точке х0 функций – есть функция, непрерывная в точке х0.
2) Частное двух непрерывных функций  – есть непрерывная функция при условии, что g(x) не равна нулю в точке х0.
– есть непрерывная функция при условии, что g(x) не равна нулю в точке х0.
3) Суперпозиция непрерывных функций – есть непрерывная функция.
Это свойство может быть записано следующим образом:
Если u = f(x), v = g(x) – непрерывные функции в точке х = х0, то функция v = g(f(x)) – тоже непрерывнаяфункция в этой точке.
Справедливость приведенных выше свойств можно легко доказать, используя теоремы о пределах.
Непрерывность некоторых элементарных функций.
1) Функция f(x) = C, C = const – непрерывная функция на всей области определения.
2) Рациональная функция  непрерывна для всех значений х, кроме тех, при которых знаменатель обращается в ноль. Таким образом, функция этого вида непрерывна на всей области определения.
непрерывна для всех значений х, кроме тех, при которых знаменатель обращается в ноль. Таким образом, функция этого вида непрерывна на всей области определения.
3) Тригонометрические функции непрерывны на своей области определения.
Докажем свойство 3 для функции y = sinx.
Запишем приращение функции Dy = sin(x + Dx) – sinx, или после преобразования:


Действительно, имеется предел произведения двух функций  и
и  . При этом функция косинус – ограниченная функция при Dх®0
. При этом функция косинус – ограниченная функция при Dх®0  , а т.к.
, а т.к.
предел функции синус  , то она является бесконечно малой при Dх®0.
, то она является бесконечно малой при Dх®0.
Таким образом, имеется произведение ограниченной функции на бесконечно малую, следовательно это произведение, т.е. функция Dу – бесконечно малая. В соответствии с рассмотренными выше определениями, функция у = sinx – непрерывная функция для любого значения х = х0 из области определения, т.к. ее приращение в этой точке – бесконечно малая величина.
Аналогично можно доказать непрерывность остальных тригонометрических функций на всей области определения.
Вообще следует заметить, что все основные элементарные функции непрерывны на всей своей области определения.
3. Точки разрыва и их классификация.
Рассмотрим некоторую функцию f(x), непрерывную в окрестности точки х0, за исключением может быть самой этой точки. Из определения точки разрыва функции следует, что х = х0 является точкой разрыва, если функция не определена в этой точке, или не является в ней непрерывной.
Следует отметить также, что непрерывность функции может быть односторонней. Поясним это следующим образом.
Если односторонний предел (см. выше)  , то функция называется непрерывной справа.
, то функция называется непрерывной справа.

х0
Если односторонний предел (см. выше)  , то функция называется непрерывной слева.
, то функция называется непрерывной слева.
 |
х0
Определение. Точка х0 называется точкой разрыва функции f(x), если f(x) не определена в точке х0 или не является непрерывной в этой точке.
Определение. Точка х0 называется точкой разрыва 1- го рода, если в этой точке функция f(x) имеет конечные, но не равные друг другу левый и правый пределы.

Для выполнения условий этого определения не требуется, чтобы функция была определена в точке х = х0, достаточно того, что она определена слева и справа от нее.
Из определения можно сделать вывод, что в точке разрыва 1 – го рода функция может иметь только конечный скачок. В некоторых частных случаях точку разрыва 1 – го рода еще иногда называют устранимой точкой разрыва, но подробнее об этом поговорим ниже.
Определение. Точка х0 называется точкой разрыва 2 – го рода, если в этой точке функция f(x) не имеет хотя бы одного из односторонних пределов или хотя бы один из них бесконечен.
Пример. Функция Дирихле (Дирихле Петер Густав(1805-1859) – немецкий математик, член- корреспондент Петербургской АН 1837г)

не является непрерывной в любой точке х0.
Пример. Функция f(x) =  имеет в точке х0 = 0 точку разрыва 2 – го рода, т.к.
имеет в точке х0 = 0 точку разрыва 2 – го рода, т.к.
 .
.


Пример. f(x) = 
Функция не определена в точке х = 0, но имеет в ней конечный предел 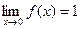 , т.е. в точке х = 0 функция имеет точку разрыва 1 – го рода. Это – устранимая точка разрыва, т.к. если доопределить функцию:
, т.е. в точке х = 0 функция имеет точку разрыва 1 – го рода. Это – устранимая точка разрыва, т.к. если доопределить функцию:

График этой функции:

Пример. f(x) =  =
= 
 y
y
0 x
-1
Эта функция также обозначается sign(x) – знак х. В точке х = 0 функция не определена. Т.к. левый и правый пределы функции различны, то точка разрыва – 1 – го рода. Если доопределить функцию в точке х = 0, положив f(0) = 1, то функция будет непрерывна справа, если положить f(0) = -1, то функция будет непрерывной слева, если положить f(x) равное какому- либо числу, отличному от 1 или –1, то функция не будет непрерывна ни слева, ни справа, но во всех случаях тем не менее будет иметь в точке х = 0 разрыв 1 – го рода. В этом примере точка разрыва 1 – го рода не является устранимой.
Таким образом, для того, чтобы точка разрыва 1 – го рода была устранимой, необходимо, чтобы односторонние пределы справа и слева были конечны и равны, а функция была бы в этой точке не определена.
4. Непрерывность функции на интервале и на отрезке.
Определение. Функция f(x) называется непрерывной на интервале (отрезке), если она непрерывна в любой точке интервала (отрезка).
При этом не требуется непрерывность функции на концах отрезка или интервала, необходима только односторонняя непрерывность на концах отрезка или интервала.
Свойства функций, непрерывных на отрезке.
Свойство 1: (Первая теорема Вейерштрасса (Вейерштрасс Карл (1815-1897)- немецкий математик)). Функция, непрерывная на отрезке, ограничена на этом отрезке, т.е. на отрезке [a, b] выполняется условие –M £ f(x) £ M.
Доказательство этого свойства основано на том, что функция, непрерывная в точке х0, ограничена в некоторой ее окрестности, а если разбивать отрезок [a, b] на бесконечное количество отрезков, которые “стягиваются” к точке х0, то образуется некоторая окрестность точки х0.
Свойство 2: Функция, непрерывная на отрезке [a, b], принимает на нем наибольшее и наименьшее значения.
Т.е. существуют такие значения х1 и х2, что f(x1) = m, f(x2) = M, причем
m £ f(x) £ M
Отметим эти наибольшие и наименьшие значения функция может принимать на отрезке и несколько раз (например – f(x) = sinx).
Разность между наибольшим и наименьшим значением функции на отрезке называется колебанием функции на отрезке.
Свойство 3: (Вторая теорема Больцано – Коши). Функция, непрерывная на отрезке [a, b], принимает на этом отрезке все значения между двумя произвольными величинами.
Свойство 4: Если функция f(x) непрерывна в точке х = х0, то существует некоторая окрестность точки х0, в которой функция сохраняет знак.
Свойство 5: (Первая теорема Больцано (1781-1848) – Коши). Если функция f(x)- непрерывная на отрезке [a, b] и имеет на концах отрезка значения противоположных знаков, то существует такая точка внутри этого отрезка, где f(x) = 0.
Т.е. если sign(f(a)) ¹ sign(f(b)), то $ х0: f(x0) = 0.
Определение. Функция f(x) называется равномерно непрерывной на отрезке [a, b], если для любого e>0 существует D>0 такое, что для любых точек х1Î[a,b] и x2Î[a,b] таких, что
ïх2 – х1ï< D
верно неравенство ïf(x2) – f(x1)ï < e
Отличие равномерной непрерывности от “обычной” в том, что для любого e существует свое D, не зависящее от х, а при “обычной” непрерывности D зависит от e и х.
Свойство 6: Теорема Кантора (Кантор Георг (1845-1918)- немецкий математик). Функция, непрерывная на отрезке, равномерно непрерывна на нем.
(Это свойство справедливо только для отрезков, а не для интервалов и полуинтервалов.)
Пример. 

Функция  непрерывна на интервале (0, а), но не является на нем равномерно непрерывной, т.к. существует такое число D>0 такое, что существуют значения х1 и х2 такие, чтоïf(x1) – f(x2)ï>e, e - любое число при условии, что х1 и х2 близки к нулю.
непрерывна на интервале (0, а), но не является на нем равномерно непрерывной, т.к. существует такое число D>0 такое, что существуют значения х1 и х2 такие, чтоïf(x1) – f(x2)ï>e, e - любое число при условии, что х1 и х2 близки к нулю.
Свойство 7: Если функция f(x) определена, монотонна и непрерывна на некотором промежутке, то и обратная ей функция х = g(y) тоже однозначна, монотонна и непрерывна.
Пример. Исследовать на непрерывность функцию и определить тип точек разрыва, если они есть.



в точке х = -1 функция непрерывна в точке х = 1 точка разрыва 1 – го рода
 у
у
-4 -1 0 1 х
Пример. Исследовать на непрерывность функцию и определить тип точек разрыва, если они есть.



в точке х = 0 функция непрерывна в точке х = 1 точка разрыва 1 – го рода
 |
у
-p -p/2 0 1 x
Лекция 4.
1. Производная функции, ее геометрический и физический смысл.
Определение. Производной функции f(x) в точке х = х0 называется предел отношения приращения функции в этой точке к приращению аргумента, если он существует.

 у
у
f(x)
f(x0 +Dx) P
Df
f(x0) M
a b Dx
0 x0 x0 + Dx x
Пусть f(x) определена на некотором промежутке (a, b). Тогда  тангенс угла наклона секущей МР к графику функции.
тангенс угла наклона секущей МР к графику функции.

 ,
,
где a - угол наклона касательной к графику функции f(x) в точке (x0, f(x0)).
Угол между кривыми может быть определен как угол между касательными, проведенными к этим кривым в какой- либо точке.

Уравнение касательной к кривой: 

Уравнение нормали к кривой:  .
.
Фактически производная функции показывает как бы скорость изменения функции, как изменяется функция при изменении переменной.
Физический смысл производной функции f(t), где t- время, а f(t)- закон движения (изменения координат) – мгновенная скорость движения.
Соответственно, вторая производная функции- скорость изменения скорости, т.е. ускорение.
2. Односторонние производные функции в точке.
Определение. Правой (левой) производной функции f(x) в точке х = х0 называется правое (левое) значение предела отношения  при условии, что это отношение существует.
при условии, что это отношение существует.


Если функция f(x) имеет производную в некоторой точке х = х0, то она имеет в этой точке односторонние производные. Однако, обратное утверждение неверно. Во- первых функция может иметь разрыв в точке х0, а во- вторых, даже если функция непрерывна в точке х0, она может быть в ней не дифференцируема.
Например: f(x) = ïxï- имеет в точке х = 0 и левую и правую производную, непрерывна в этой точке, однако, не имеет в ней производной.
Теорема. (Необходимое условие существования производной) Если функция f(x) имеет производную в точке х0, то она непрерывна в этой точке.
Понятно, что это условие не является достаточным.
3. Основные правила дифференцирования.
Обозначим f(x) = u, g(x) = v - функции, дифференцируемые в точке х.
1) (u ± v)¢ = u¢ ± v¢
2) (u×v)¢ = u×v¢ + u¢×v
3)  , если v ¹ 0
, если v ¹ 0
Эти правила могут быть легко доказаны на основе теорем о пределах.
Производные основных элементарных функций.
1)С¢ = 0; 9) 
2)(xm)¢ = mxm-1; 10) 
3)  11)
11) 
4)  12)
12) 
5)  13)
13) 
6)  14)
14) 
7) 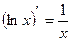 15)
15) 
8)  16)
16) 
4. Производная сложной функции.
Теорема. Пусть y = f(x); u = g(x), причем область значений функции u входит в область определения функции f.

Тогда 
Доказательство.


(с учетом того, что если Dx®0, то Du®0, т.к. u = g(x) – непрерывная функция)
Тогда 
Теорема доказана.
5. Производная показательно- степенной функции.
Функция называется показательной, если независимая переменная входит в показатель степени, и степенной, если переменная является основанием. Если же и основание и показатель степени зависят от переменной, то такая функция будет показательно – степенной.
Пусть u = f(x) и v = g(x) – функции, имеющие производные в точке х, f(x)>0.
Найдем производную функции y = uv. Логарифмируя, получим:
lny = vlnu




Пример. Найти производную функции  .
.
По полученной выше формуле получаем: 
Производные этих функций: 
Окончательно:

6. Производная обратных функций.
Пусть требуется найти производную функции у = f(x) при условии, что обратная ей функция x = g(y) имеет производную, отличную от нуля в соответствующей точке.
Для решения этой задачи дифференцируем функцию x = g(y) по х:

т.к. g¢(y) ¹ 0 


т.е. производная обратной функции обратна по величине производной данной функции.
Пример. Найти формулу для производной функции arctg.
Функция arctg является функцией, обратной функции tg, т.е. ее производная может быть найдена следующим образом:

Известно, что 
По приведенной выше формуле получаем:

Т.к.  то можно записать окончательную формулу для производной арктангенса:
то можно записать окончательную формулу для производной арктангенса:

Таким образом получены все формулы для производных арксинуса, арккосинуса и других обратных функций, приведенных в таблице производных.
7. Дифференциал функции.
Пусть функция y = f(x) имеет производную в точке х:

Тогда можно записать:  , где a®0, при Dх®0.
, где a®0, при Dх®0.
Следовательно:  .
.
Величина aDx- бесконечно малая более высокого порядка, чем f¢(x)Dx, т.е. f¢(x)Dx- главная часть приращения Dу.
Определение. Дифференциалом функции f(x) в точке х называется главня линейная часть приращения функции.
Обозначается dy или df(x).
Из определения следует, что dy = f¢(x)Dx или

dy = f¢(x)dx.
Можно также записать: 
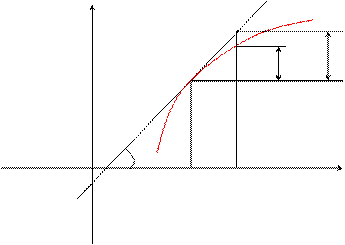
8. Геометрический смысл дифференциала.
 y
y
f(x)
K
dy
M Dy
L
a
x x + Dx x
Из треугольника DMKL: KL = dy = tga×Dx = y¢×Dx
Таким образом, дифференциал функции f(x) в точке х равен приращению ординаты касательной к графику этой функции в рассматриваемой точке.
9. Свойства дифференциала.
Если u = f(x) и v = g(x)- функции, дифференцируемые в точке х, то непосредственно из определения дифференциала следуют следующие свойства:
1) d(u ± v) = (u ± v)¢dx = u¢dx ± v¢dx = du ± dv
2) d(uv) = (uv)¢dx = (u¢v + v¢u)dx = vdu + udv
3) d(Cu) = Cdu
4) 
10. Дифференциал сложной функции.
Инвариантная форма записи дифференциала.
Пусть y = f(x), x = g(t), т.е у- сложная функция.

Тогда dy = f¢(x)g¢(t)dt = f¢(x)dx.
Видно, что форма записи дифференциала dy не зависит от того, будет ли х независимой переменной или функцией какой- то другой переменной, в связи с чем эта форма записи называется инвариантной формой записи дифференциала.
Однако, если х- независимая переменная, то
dx = Dx, но
если х зависит от t, то Dх ¹ dx.
Таким образом форма записи dy = f¢(x)Dx не является инвариантной.
Пример. Найти производную функции  .
.
Сначала преобразуем данную функцию: 

Пример. Найти производную функции  .
.

Пример. Найти производную функции 

Пример. Найти производную функции 

Пример. Найти производную функции 

11. Формула Тейлора.






