Таблица 2.1
Частные критерии для продольного канала
| № кри-терия | Наименование, размерность | Математическое выражение | Весовой коэффи- циент |
 1
| Усредненное за период Т отклонение директорной стрелки продольного канала, мм 2. |
| |
 2
| Усредненная скорость отклонения тангажа, град 2/ с 2 |
| |
 3
| Усредненная скорость отклонения рукоятки управления по тангажу, мм 2/ с 2 |
| |
 4
| Усредненная перегрузка |
| |
| Ошибка по высоте в точке конца режима, м |
| ||
   6
| Ошибка по вертикальной скорости в точке конца режима, м/с |
| |
| Максимальное отклонение пульса летчика от номинала, ударов /мин |
|
Выделенные показатели представляют собой исходную совокупность частных критериев, из которых формируется комплексный критерий качества технической эргатической системы управления.
Наиболее употребимая форма представления обобщенного критерия качества такова:
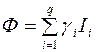, (2.1)
где Ii - частные критерии качества;
- весовые коэффициенты;
q - количество частных критериев.
Таблица 2.2
Частные критерии для бокового канала
| № кри-терия | Наименование, размерность | Математическое выражение | Весовой коэффи- циент |
| Усредненное за период Т отклонение директорной стрелки бокового канала, мм 2. | 
|
| |
| Усредненная скорость отклонения крена, град 2 | 
|
| |
| Усредненная скорость отклонения рукоятки управления по крену, мм 2/ с 2 | 
|
| |
| Усредненная перегрузка | 
|
| |
| Боковое отклонение в точке конца режима, м | 
|
| |
| Ошибка по боковой скорости в точке конца режима, м/с | 
|
| |
| Максимальное отклонение пульса летчика от номинала, ударов /мин | 
|
|
Формула (2.1) предусматривает, что все частные критерии требуют минимизации (или максимизации). Весовые коэффициенты имеют размерность, представляющую собой дробь, в числителе которой находиться размерность обобщенного критерия, а в знаменателе – размерность i -го частного критерия.
Более удобным представляются такие формы обобщенного критерия, при которых весовые коэффициенты являются безразмерными. Без потери общности безразмерный обобщенный критерий можно представить в виде:
, (2.2)
где mi – масштабные коэффициенты. В обычной практике масштабные коэффициенты рассчитываются по формуле:
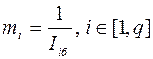, (2.3)
где q – количество частных критериев; Iiб – базовые значения для i -го частного критерия. В качестве базового обычно принимается либо номинальное, либо предельно допустимое значение соответствующего частного критерия.
При этом все частные критерии в выражении (2.2) считаются, например, требующими минимизации. Если же какой то из них, например Jk требует максимизации, то вместо него вводиться частный критерий Ik= (-Jk), который должен минимизироваться. Поэтому выражение (2.2) является общим.
