Важной задачей, возникающей при анализе ряда динамики, является установление основной тенденции изменения уровней, присущих данному ряду.
Уровни ряда динамики формируются под влиянием множества длительно и кратковременно действующих факторов и в том числе различного рода случайных обстоятельств. Выявление основной тенденции развития (тренда) называется в статистике выравниванием временного ряда.
Одним из наиболее простых приемов обнаружения общей тенденции развития является – укрупнение интервала динамического ряда. Основан на укрупнении периодов времени, к которым относят уровни ряда. Например, ряд ежесуточного выпуска продукции заменятся рядом месячного выпуска продукции и т.п.
Выявление основной тенденции может быть осуществлено также методом скользящей средней. Основан на том, что вычисляется средний уровень из определенного числа первых по порядку уровней ряда, затем средний уровень из такого же числа уровней, начиная со второго, далее – начиная с третьего и т.д. При сглаживании скользящей средней технически удобнее укрупненный интервал составить из нечетного числа уровней ряда.
Покажем применение скользящей средней уровней ряда динамики на следующем примере.
Пример. На основе данных об урожайности зерновых культур в хозяйстве за 1995—2009 гг. проведем сглаживание ряда методом скользящей средней.
Динамика урожайности зерновых культур в хозяйстве за 1995—2009 гг. и расчет скользящих средних
| Год | Урожайность зерно-вых, ц/га | Трехлетние Сколь-зящие суммы | Трехле-тние Сколь-зящие средние | Четырех-летние Скользя-щие суммы | Четырехлет-ние скользящие средние (нецентрированные)* | Четырех-летние скользя-щие средние (центрированные) |
| А | ||||||
| 1995 | 19,5 | — | — | — | ||
| 23,4 | - | 22,6 | - | 22,5 | — | |
| 25,0 | 67,9 | 23,6 | - | 24,1 | 23,3 | |
| 22,4 | 70,8 | 24,3 | 90,3 | 25,4 | 24,8 | |
| 25,5 | 72,9 | 25,6 | 96,3 | 25,8 | 25,6 | |
| 28,8 | 76,7 | 27,0 | 101,7 | 27,8 | 26,8 | |
| 26,6 | 80,9 | 28,6 | 103,3 | 26,6 | 27,2 | |
| 30,4 | 85,8 | 25,9 | 111,3 | 28,4 | 27,5 | |
| 20,7 | 77,7 | 29,0 | 106,5 | 30,7 | 26,6 | |
| 35,8 | 86,9 | 30,8 | 113,5 | 29,5 | 30,3 | |
| 36,0 | 92,5 | 32,5 | 122,9 | 32,5 | 31,0 | |
| 25,6 | 97,4 | 31,4 | 118,1 | 32,3 | 32,4 | |
| 32,5 | 94,1 | 31,0 | 129,9 | 30,1 | 31,2 | |
| 35,0. | 94,7 | 3t,6 | 129,1 | — | — | |
| 27,2 | 94,7 | - | 120,3 | — | — |
*По графе 5 значения показателей находятся в промежутке между годами.
Суть метода скользящей средней состоит в том, что вычисляется средний уровень из определенного числа первых по порядку уровней ряда, затем — средний уровень из того же числа уровней, начиная со второго, далее — начиная с третьего и т.д. Таким образом, при расчетах среднего уровня как бы «скользят» по ряду динамики от его начала к концу, каждый раз отбрасывая один уровень в начале и добавляя один следующий.
Средняя из нечетного числа уровней относится к середине интервала. Если интервал сглаживания четный, то отнесение средней к определенному времени невозможно, она относится к середине между датами. Для того чтобы правильно отнести среднюю из четного числа уровней, применяется центрирование, т.е. нахождение средней из средней, которую относят уже к определенной дате.
1. Рассчитаем трехлетние скользящие суммы.
Находим сумму урожайности за 1995—1997 гг.: 19,5 + 23,4 + 25,0 = 67,9 и записываем это значение в 1997 г. Затем из этой суммы вычитаем значение показателя за 1995 г. и прибавляем показатель за 1998 г.: 67,9 - 19,5 + 22,4 - 70,8 и это значение записываем в 1998 г. и т.д.
2. Определим трехлетние скользящие средних по формуле простой
средней арифметической:
.
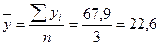Полученное значение записываем в 1996 г. Затем берем следующую трехлетнюю скользящую сумму и находим трехлетнюю скользящую среднюю: 70,8: 3 - 23,6, полученное значение записываем в 1997 г. и т.д.
Аналогичным образом рассчитываются четырехлетние скользящие суммы. Их значения представлены в графе 4 таблицы данного гримера.
Четырехлетние скользящие средние определяются по формуле простой средней арифметической:
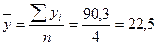
Это значение будет отнесено между двумя годами —1996 и 1997 гг., т.е. в середине интервала сглаживания. Для того чтобы найти четырехлетние скользящие средние центрированные, необходимо найти среднюю из двух смежных скользящих средних:
.
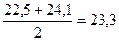Эта средняя будет отнесена к 1997 г. Аналогичным образом рассчитываются остальные центрированные средние; их значения записываются в графу 6 таблицы данного примера.
Недостаток метода простой скользящей средней состоит в том, что сглаживаемый ряд динамики сокращается ввиду невозможности получить сглаженный уровень для начала и конца ряда. Этот недостаток устраняется применением ряда аналитического выравнивания.
Аналитическое выравнивание предполагает представление уравнения данного ряда динамики в виде функции времени
Y = f (t), где
Y – уровни динамического ряда, вычисленные по соответствующему аналитическому уравнению на момент времени t.
Для отображения основной тенденции развития явлений во времени применяются различные функции:
- линейная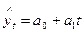 
- парабола второго порядка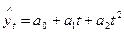 
- кубическая парабола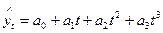 
- показательная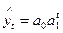 
- экспоненциальная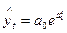 
- модифицированная экспонента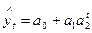 
- логарифмическая парабола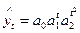 
- гиперболическая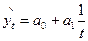 
и др.
Выбор формы кривой во многом определяют результаты экстраполяции тренда (продлении в будущее тенденции, наблюдавшейся в прошлом). На практике часто используют графическое изображение уровней динамического ряда, но при этом целесообразно пользоваться графическим изображением сглаженных уровней.
При выборе вида кривой можно воспользоваться методом конечных разностей, используя следующие их свойства:
- если общая тенденция выражается линейным уравнением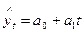 
, то постоянными являются первые разности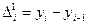 
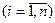, а нулевыми вторые разности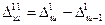 
;
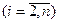- если тенденции выражаются параболой второго порядка 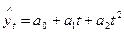, то постоянными являются вторые разности, а третьи являются нулевыми.
Из других признаков, которые могут применяться при выборе формы кривой можно рекомендовать:
- если примерно постоянными оказываются темпы роста, то для выравнивания применяется показательная функция;
- если первые разности имеют тенденцию уменьшаться с постоянным темпом, то следует остановиться на модифицированной экспоненте;
- если средние уровни, нанесенные на полулогарифмическую сетку, близки к прямой линии, то предпочтительной является простая экспонента.
Выбор формы кривой может осуществляться и на основе принятого критерия, в качестве которого может служить сумма квадратов отклонений фактических значений от значений, рассчитанных по уравнению тренда. Из всей совокупности кривых выбирается та, которой соответствует минимальное значение критерия.
Согласно этому критерию, для нахождения параметров полинома к-ой степени необходимо решить систему так называемых нормальных уравнений:
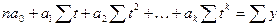
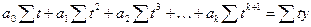
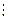
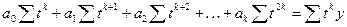
n- число членов в ряде динамики;
t – условный параметр времени .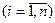
Система содержит в качестве известных величин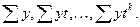 
.Решением системы являются параметры 
.
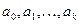Система нормальных уравнений для оценивания параметров прямой 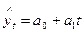примет вид:
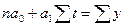
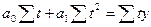
Параметры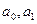 
будут находиться по формулам:
, 
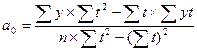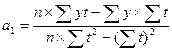
В статистической практике применяется упрощенный расчет параметров уравнений, который заключается в переносе начала координат в середину ряда динамики. В этом случае упрощаются сами нормальные уравнения. Действительно, если до переноса начала координат t принимало значения 1,2,3, ……, n, то после переноса t = …-4, -3, -2, -1, 0, 1, 2, 3, 4,..., если же число членов ряда четное, то t =...,-5, -3,-1,1,3,5,….Следовательно,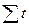 
и все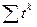 
, у которых «к» - нечетное число, равны нулю. Система нормальных уравнений для уравнения прямой будет:
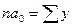
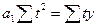
Для параболы второго порядка система нормальных уравнений для нахождения параметров модели примет вид:
,
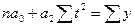
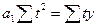
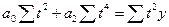где параметр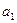 
, выражает начальную скорость роста, а коэффициент 
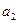- постоянную скорость изменения прироста.
Рассмотрим применение метода аналитического выравнивания по прямой для выражения основной тенденции на примере.
Пример. Исходные и расчетные данные определения параметров уравнения прямой.
| Год | Урожайность зерновых, ц/га | t | t2 | ty |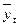 
| 
| 
|
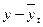
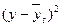
| А | |||||||
| 1995 | 19,5 | -7 | -136,5 | 22,0 | -2,5 | 6,25 | |
| 23,4 | -6 | -140,4 | 22,8 | 0,6 | 0,36 | ||
| 25,0 | -5 | -125,0 | 23,6 | 1,4 | 1,96 | ||
| 22,4 | -4 | -89,6 | 24,4 | -2,0 | 4,00 | ||
| 25,5 | -3 | -76,5 | 25,2 | 0,3 | 0,09 | ||
| 28,8 | -2 | -57,6 | 26,0 | 2,8 | 7,84 | ||
| 26,6 | -1 | -26,6 | 26,8 | -0,2 | 0,04 | ||
| 30,4 | 27,6 | 2,8 | 7,84 | ||||
| 20,7 | +1 | 20,7 | 28,4 | -7,7 | 59,29 | ||
| 35,8 | +2 | 71,6 | 29,2 | 6,6 | 43,56 | ||
| 36,0 | +3 | 108,0 | 30,0 | 6,0 | 36,00 | ||
| 25,6 | +4 | 102,4 | 30,8 | -5,2 | 27,04 | ||
| 32,5 | +5 | 162,5 | 31,6 | 0,9 | 0,81 | ||
| 35,0 | +6 | 210,0 | 32,4 | 2,6 | 6,76 | ||
| 27,2 | +7 | 190,4 | 33,2 | -6,0 | 36,00 | ||
| Итого | 414,4 | - | 213,4 | 414,4 | - | 237,84 |
Уравнение прямой при аналитическом выравнивании ряда динамики имеет следующий вид:
,
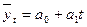где 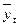— выравненный (средний) уровень динамического ряда;
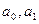— параметры искомой прямой; t — условное обозначение времени.
Способ наименьших квадратов дает систему двух нормальных уравнений для нахождения параметров a 0 и a 1:
,
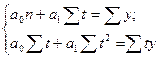где у — исходный уровень ряда динамики;
п — число членов ряда.
Система уравнений упрощается, если значения t подобрать так, чтобы их сумма равнялась нулю, т.е. начало времени перенести в середину рассматриваемого периода.
Если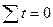 
, 
, 
.
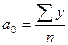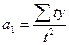Расчет необходимых значений дан в таблице примера. По итоговым данным определяем параметры уравнения:
; 
.
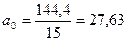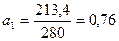Уравнение прямой будет иметь вид: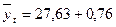 
.
Подставляя в уравнение принятые обозначения t, вычислим выравненные уровни ряда динамики (см. значения 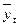в таблице).
На основе данных таблицы рассчитаем показатели колеблемости динамических рядов, которые характеризуются средним квадратическим отклонением и коэффициентом вариации.
Среднее квадратическое отклонение можно измерить по формуле:
.
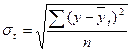Используя данные нашего примера, рассчитаем показатель колеблемости урожайности зерновых культур за анализируемый период:
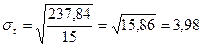(ц).
Коэффициент вариации исчисляется по формуле:
.
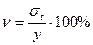В нашем примере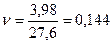 
, или 14,4%.
Исследование динамики социально-экономических явлений и установление основной тенденции развития дают основание для прогнозирования (экстраполяции) — определения будущих размеров уровня экономического явления. Используют следующие методы экстраполяции:
· средний абсолютный прирост;
· средний темп роста;
· экстраполяцию на основе выравнивания по какой-либо аналитической формуле.
