Приложение №1
Задача №1.
Опрос 100 студентов дал следующие результаты о количестве студентов, изучающих различные иностранные языки: испанский – 28, немецкий – 30, французский – 42, испанский и немецкий – 8, испанский и французский – 10, немецкий и французский – 5, все три языка – 3.
Сколько студентов не изучает ни одного языка?
Сколько студентов изучает один французский язык?
Задача №2.
Опрос 100 студентов дал следующие результаты о количестве студентов, изучающих различные иностранные языки: только немецкий –18, немецкий, но не испанский – 23, немецкий и французский – 8, немецкий – 26, французский – 48, испанский и французский – 8,.
Сколько студентов изучает испанский и немецкий языки?
Сколько студентов изучает испанский язык?
Приложение №2
Пример
Вычислить определитель матрицы:
| п | ||||
где п порядковый номер обучающегося в журнале группы.
Приложение №3
Решить системы уравнений методом обратной матрицы:
А) { x+2y-3z=-3
{-2x+6y+9z=-11
{-4x-3y+8z=-2
B) {3x=y-z=10
{-3x+3y+2z=8
{5x+2y+8z=-1
Приложение №4
Вариант 1.
1. Даны векторы  Найдите координаты вектора
Найдите координаты вектора  .
.
2. Вершины треугольника АВС имеют координаты А(5;1;4), В(2;3;6), С(6;3;5). Определите вид треугольника (равнобедренный, равносторонний, остроугольный, …) и найдите длину медианы, проведенной к стороне ВС.
3. Даны точки А(1;2;2), В(2;5;0), С(3;7;1), D(2;4;3). Определите вид четырехугольника ABCD.
Вариант 2.
1. Даны векторы  Найдите координаты вектора 3
Найдите координаты вектора 3  .
.
2. Вершины треугольника АВС имеют координаты А(1;3;10), В(4;2;3), С(8;7;4). Определите вид треугольника (равнобедренный, равносторонний, остроугольный, …) и найдите длину медианы, проведенной к стороне АС.
3. Даны точки А(2;1;5), В(6;1;4), С(7;4;8), D(3;4;9). Определите вид четырехугольника ABCD.
Вариант 3
1. Даны векторы  Найдите координаты вектора
Найдите координаты вектора  .
.
2. Вершины треугольника АВС имеют координаты А(1;-1;3), В(3;-1;1), С(-1;1;3). Найдите углы треугольника, его периметр и площадь.
3. Даны точки А(2;8;1), В(3;3;2), С(4;1;5), D(5;2;10). Определите вид четырехугольника ABCD и найдите длины его диагоналей.
Приложение №5
Вариант 1
1. Угловой коэффициент к и нормальный вектор  прямой
прямой  соответственно равны:
соответственно равны:
а) к =  ;
;  = {2, −3};
= {2, −3};
в) к =  ;
;  = {3, −2};
= {3, −2};
с) к = −  ;
;  = {3, 2};
= {3, 2};
d) к =  ;
;  = {−3, 2}.
= {−3, 2}.
2. Составить уравнение прямой, проходящей через точку  :
:
а) параллельно прямой  ;
;
б) перпендикулярно прямой  .
.
3. Даны уравнения кривых 2го порядка:
1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  ;
;
5) 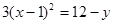 .
.
Уравнению гиперболы соответствуют
а) 1, 2; в) 1, 4; с) 1, 4, 5; d) 1, 5.
4. Дано уравнение эллипса  . Найдите его большую и малую полуоси. Постройте этот эллипс.
. Найдите его большую и малую полуоси. Постройте этот эллипс.
Вариант 2
1. Нормальный вектор  прямой, проходящей через точки М1 (2, 3) и
прямой, проходящей через точки М1 (2, 3) и
М2 (4, 5) имеет координаты:
а)  = {1, −2}; в)
= {1, −2}; в)  = {1, −1}; с)
= {1, −1}; с)  = {2, 1}; d)
= {2, 1}; d)  = {1, 0}.
= {1, 0}.
2. Составить уравнение прямой, проходящей через точку  :
:
а) параллельно прямой  ;
;
б) перпендикулярно прямой  .
.
3. Координаты центра С и радиус R окружности  соответственно равны:
соответственно равны:
а) С (2, 1), R = 2;
в) С (2, −1), R = 3;
с) С (−2, −1), R = 3;
d) С (−2, 1), R = 2.
4.Среди заданных кривых гиперболой является:
а)  ; в)
; в)  ; с)
; с)  ; d)
; d)  .
.
Постройте эту гиперболу.
Приложение №6
Вариант 1.
1. Запишите 5 первых членов последовательности, заданной общим членом  :
:
А) 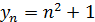
Б) 
В) 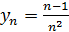
Являются ли данные последовательности монотонными, ограниченными?
2. Найдите область определения функций:
а) 
б) 
3. Постройте последовательно графики функций:
а)  и
и 
б)  и
и 
4. Для функции из №3(б) выпишите основные свойства.
Вариант 2.
1. Запишите 5 первых членов последовательности, заданной общим членом  :
:
А) 
Б) 
В) 
Являются ли данные последовательности монотонными, ограниченными?
2. Найдите область определения функций:
а) 
б) 
3. Постройте последовательно графики функций:
а)  и
и 
б)  и
и 
4. Для функции из №3(б) выпишите основные свойства.
Приложение №7
Вариант 1.
Вычислите пределы функций:
1. 
2. 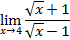
Раскройте неопределенности и вычислите пределы:
3. 
4. 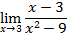
Вычислите пределы, используя «замечательные пределы»:
5. 
6. 
Вариант 2.
Вычислите пределы функций:
1. 
2. 
Раскройте неопределенности и вычислите пределы:
3. 
4. 
Вычислите пределы, используя «замечательные пределы»:
5. 
6. 
Приложение №8
Вариант 1.
1. Вычислите производную функции:
а) 
б) 
в)  в точке
в точке  .
.
2. Найдите наибольшее и наименьшее значения функции  на промежутке
на промежутке  .
.
3. Запишите уравнение касательной к графику функции  в точке
в точке  .
.
4. Точка движется по закону  (м). Найдите скорость и ускорение точки в момент времени
(м). Найдите скорость и ускорение точки в момент времени  .
.
Вариант 2.
1. Вычислите производную функции:
а) 
б) 
в)  в точке
в точке  .
.
2. Найдите наибольшее и наименьшее значения функции  на промежутке
на промежутке  .
.
3. Запишите уравнение касательной к графику функции  в точке
в точке  .
.
4. Точка движется по закону 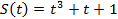 (м). Найдите скорость и ускорение точки в момент времени
(м). Найдите скорость и ускорение точки в момент времени  .
.
Приложение №9
Вариант 1.
1. Найдите промежутки возрастания и убывания функции  .
.
2. Найдите наибольшее и наименьшее значения функции  на промежутке
на промежутке  .
.
3. Исследуйте функцию  и постройте ее график.
и постройте ее график.
Вариант 2.
1. Найдите промежутки возрастания и убывания функции  .
.
2. Найдите наибольшее и наименьшее значения функции  на промежутке
на промежутке  .
.
3. Исследуйте функцию  и постройте ее график.
и постройте ее график.
Приложение №10
Приложение №11
Вариант 1.
1. Вычислите неопределенный интеграл:
а)  ;
;
б)  ;
;
в) 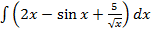 .
.
2. Вычислите определенные интегралы:
а) 
б)  .
.
3. Найдите площадь фигуры, ограниченной линиями  и
и 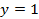 .
.
Вариант 2.
1. Вычислите неопределенный интеграл:
а)  ;
;
б)  ;
;
в)  .
.
2. Вычислите определенные интегралы:
а) 
б)  .
.
3. Найдите площадь фигуры, ограниченной линиями  ,
,  и
и 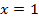 .
.
Вариант 3.
1. Вычислите неопределенный интеграл:
а)  ;
;
б)  ;
;
в)  .
.
2. Вычислите определенные интегралы:
а) 
б) 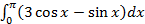 .
.
3. Найдите площадь фигуры, ограниченной линиями 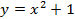 ,
,  и
и 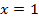 .
.
Приложение №12
Вариант 1.
Вычислите частные производные  и
и  функции
функции  :
:
а) 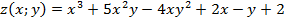
б) 
Вариант 2.
а) 
б) 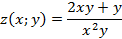
Приложение №13
Вариант 1
1) Исследовать ряды на сходимость:
А)  ; В)
; В)  ;
;
Б)  ; Г)
; Г)  ;
;
Д)  ; Е)
; Е)  ;
;
2) Найти область сходиомсти ряда 
3) Найти круг сходимости ряда 
Вариант 2
1) Исследовать ряды на сходимость:
А)  ; Б)
; Б) 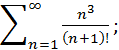
В) 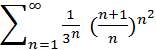 ; Г)
; Г)  ;
;
Д)  ; Е)
; Е)  ;
;
2) Найти область сходиомсти ряда 

3) Найти круг сходимости ряда 

Приложение№14
Вариант 1.
Решите дифференциальное уравнение в полных дифференциалах:

Вариант 2.
Решите дифференциальное уравнение в полных дифференциалах:

Приложение№15
Вариант 1.
Вычислите определенный интеграл
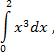
по одной из формул приближенного вычисления (по формуле прямоугольников, трапеций или парабол), разбив отрезок интегрирования [0;2] на 4 части.
Вариант 2.
Вычислите определенный интеграл

по одной из формул приближенного вычисления (по формуле прямоугольников, трапеций или парабол), разбив отрезок интегрирования [0;2] на 4 части.




