Задача 1. Запишите формулы для следующих суперпозиций:
1) 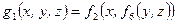 ,
,
2) 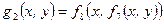 ,
,
3) 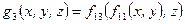 ,
,
4) 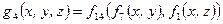 .
.
Составьте таблицы истинности и найдите наиболее простую булеву формулу.
Задача 2. Проверьте, будут ли равносильными следующие формулы.
1) 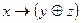 и
и 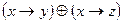 ,
,
2) 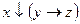 и
и 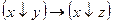 ,
,
3) 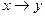 и
и 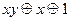 ,
,
4) 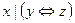 и
и 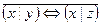 .
.
Задача 3. Упростите формулы, используя равносильные преобразования.
1) 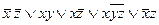 ,
,
2) 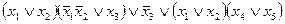 ,
,
3) 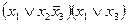 ,
,
4) 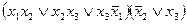 .
.
Задача 4. Запишите булевы формулы для функций 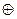 ,
, 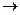 ,
, 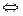 ,
,  ,
, 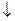 .
.
Задача 5. Запишите СДНФ и СКНФ для функций
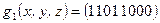 ,
, 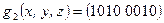 ,
,
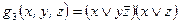 ,
, 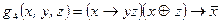 .
.
КОНТАКТНЫЕ СХЕМЫ. МИНИМИЗАЦИЯ
Задача 1. Упростите контактные схемы, используя равносильные преобразования.
1) 2)
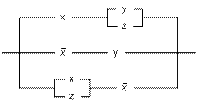
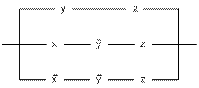
3) 4)
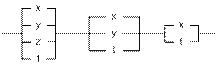

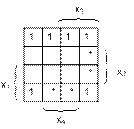
Задача 2. Постройте СДНФ по карте Карно и упростите ее до ДНФ.
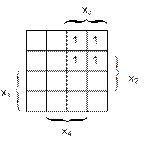
Задача 3. Минимизируйте ДНФ и КНФ по карте Карно.
1) 2)
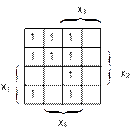
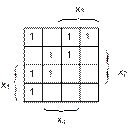
3) 4)
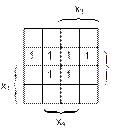
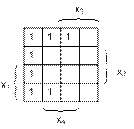
Задача 4. Минимизируйте ДНФ и КНФ для неполностью определенных переключательных функций.
1) 2)
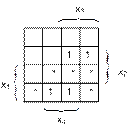
Задача 5. Запишите число 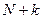 и, добавив недостающие слева нули, получите векторное задание функции
и, добавив недостающие слева нули, получите векторное задание функции 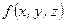 .
.
1). Постройте для этой функции а) таблицу, б) множество 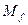 , в) карту Карно.
, в) карту Карно.
2). Найдите СДНФ, СКНФ, минимальные ДНФ и КНФ.
3). Постройте наиболее простую контактную схему, реализующую эту функцию.
Дополнительные задачи
1. Требуется, чтобы включение света в комнате осуществлялось с помощью трех различных выключателей таким образом, чтобы нажатие на любой из них приводило к включению света, если он перед этим был выключен, и к его выключению, если он был включен.
2. Пусть каждый из членов комитета голосует «за» нажатием на кнопку. Постройте по возможности наиболее простую электрическую цепь, через которую ток проходил бы тогда и только тогда, когда не менее двух членов комитета голосуют «за».
12. ТИПЫ БУЛЕВЫХ ФУНКЦИЙ. ПОЛИНОМЫ ЖЕГАЛКИНА
Задача 1. Представьте следующие функции полиномами Жегалкина. Проверьте принадлежность их к классам 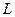 ,
, 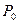 и
и 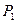
1) 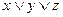 , 2)
, 2) 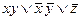 , 3)
, 3) 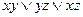 , 4)
, 4) 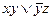 , 5)
, 5) 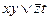 , 6)
, 6) 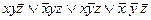 , 7)
, 7) 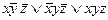 , 8)
, 8) 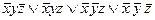 , 9)
, 9) 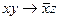 , 10)
, 10) 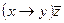 , 11)
, 11) 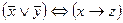 , 12)
, 12) 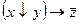 , 13)
, 13) 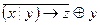 , 14)
, 14) 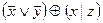 , 15)
, 15) 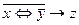 , 16)
, 16) 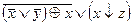 , 17)
, 17) 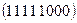 , 18)
, 18) 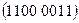 , 19)
, 19) 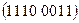 , 20)
, 20) 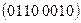 .
.
Задача 2. Выпишите все пары сравнимых между собой наборов для функции трех переменных.
Задача 3. Определите, являются ли монотонными следующие функции
1) 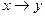 , 2)
, 2) 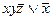 , 3)
, 3) 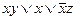 , 4)
, 4) 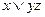 , 5)
, 5) 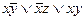 , 6)
, 6) 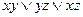 , 7)
, 7) 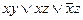 , 8)
, 8) 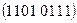 , 9)
, 9) 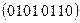 , 10)
, 10) 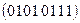 , 11)
, 11) 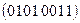 , 12)
, 12) 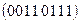 , 13)
, 13) 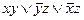 , 14)
, 14) 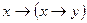 , 15)
, 15) 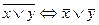 , 16)
, 16) 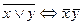 , 17)
, 17) 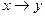 .
.
Задача 4. Найдите двойственные для следующих функций. Какие из них являются самодвойственными?
1) 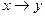 , 2)
, 2) 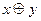 , 3)
, 3) 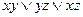 , 4)
, 4) 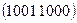 , 5)
, 5) 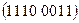 , 6)
, 6) 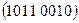 , 7)
, 7) 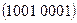 .
.
Задача 5. Докажите, что функция 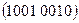 образует функционально полную систему.
образует функционально полную систему.
Задача 6. Проверьте полноту системы функций. В случае полноты определите, является ли система базисом. Укажите базис.
1) 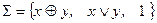 , 2)
, 2) 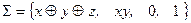 , 3)
, 3) 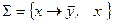 , 4)
, 4) 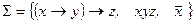 .
.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Баврин И.И. Дискретная математика. М.: Высш. шк., 2007. 200 с.
2. Белоусов А.И., Ткачев С.Б. Дискретная математика. М.: МГТУ, 2004. 744 с.
3. Зарецкая М.А. Дискретная математика для программистов. Магнитогорск: МГТУ, 2009. 172 с.
4. Зарецкая М.А., Файнштейн А.С. Метод математической индукции и комбинаторика. Методическая разработка для студентов специальности 230105. Магнитогорск: МГТУ, 2008.
5. Краснов М.Л., Киселев А.И., Макаренко Г.И. и др. Вся высшая математика, т. 7. — М.: Эдиториал УРСС, 2004. 208 с.
6. Кузнецов О.П. Дискретная математика для инженера. СПб.: Лань, 2004. 370 с.
7. Шевелев Ю.П. Дискретная математика. СПб.: Лань, 2008. 592 с.






