Одной из возможных реализаций системы СДЦ является цифровая обработка сигналов. При этом, в цифровом виде может быть реализована компенсационная часть системы (череспериодное вычитание).

Наиболее просто осуществить в цифровом виде ЧПВ на видеочастоте, что снижает требования к быстродействию процессора. Схема ЧПВ при этом имеет вид, изображенный на рис.4.120.
Задержка на период, при череспериодном вычитании, осуществляется записью цифрового кода, соответствующего амплитудам видеоимпульсов с выхода фазового детектора, в память и извлечением его из памяти через время Тп. Операция вычитания реализуется в арифметическом устройстве, в соответствии с программой вычислений. Алгоритм схемы однократного ЧПВ можно представить в виде, изображенном на рис.4.121, а.
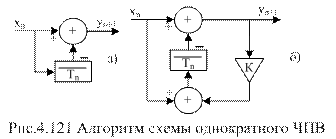
На рис.4.121, б изображена схема, с помощью которой возможна реализация однократного ЧПВ. В этом алгоритме задерживается на период повторения не код на входе хп, а разность хп– k×yn.
Такая обработка использует на каждом последующем шаге не только входной сигнал, но и результаты вычислений на предыдущем шаге. Такой алгоритм называется рекурсивным.
Алгоритм, который не использует на последующих шагах результаты вычислений на предыдущих шагах, называется нерекурсивным.
Рекурсия в алгоритме аналогична обратной связи в аналоговой схеме ЧПВ. Она позволяет корректировать форму амплитудно-частотной характеристики в полосе пропускания.
Цифровая система СДЦ позволяет реализовать фильтры второго и более высоких порядков. Это позволяет получить очень высокие значения коэффициента подпомеховой видимости. Реализация схем ЧПВ высоких порядков в аналоговой форме затруднена, так как для этого необходимо иметь идентичные линии задержки и для выравнивания АЧХ в полосе пропускания прецезионные усилители.
В цифровой схеме ЧПВ задержка осуществляется записью числа в память и извлечением его из памяти через время Тп. Усиление в цифровом виде осуществляется умножением. Если в аналоговом виде добиться точности в стабильности коэффициента усиления 1% очень трудно, то в цифровом виде точность определяется числом разрядов цифрового кода и достигает значительных величин. Это позволяет реализовать системы СДЦ в цифровом виде высоких порядков.
На рис.4.122. изображена структурная схема двухканального подавителя.

На выходах квадратурных каналов системы СДЦ имеются два выходных сигнала Ucos и Usin, полученных как результат разложения входного сигнала с помощью квадратурных фазовых детекторов на ортогональные составляющие. Для восстановления исходного (с учетом обработки) сигнала необходимо выполнить обратную операцию – получение модуля сигнала из его составляющих Ucos и Usin в соответствии с выражением
 .
.
Непосредственное вычисление модуля сопряжено с рядом неоправданных аппаратных усложнений. Поэтому при практической реализации пользуются приближенными вычислениями. Наиболее распространенный алгоритм следующий:
 (4.64)
(4.64)
Данный алгоритм проще в реализации, хотя и имеет погрешность в оценке величины выходного сигнала до 10%. Реализация формирователя модуля предусматривает следующие операции:
– сравнение входных сигналов Ucos и Usin по величине;
– фиксацию текущего значения сигнала Ucos или Usin в зависимости от результата сравнения;
– деление зафиксированного значения сигнала на два;
– суммирование.
Один из возможных вариантов реализации описанного алгоритма изображен на рис.4.123.

В качестве элементной базы используются части цифровой схемотехники.






