Скалярным произведением двух векторов( и
и  ) называется число, равное произведению модулей этих векторов на косинус угла между ними.
) называется число, равное произведению модулей этих векторов на косинус угла между ними.  Из формулы следует, что
Из формулы следует, что  , если
, если 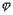 - острый угол,
- острый угол,  , если
, если  - тупой угол;
- тупой угол;  в том и только в том случае, когда векторы
в том и только в том случае, когда векторы 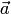 и
и  перпендикулярны (в частности
перпендикулярны (в частности 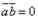 ,, если
,, если 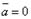 или
или  ). Скалярное произведение
). Скалярное произведение  называется скалярным квадратом вектора и обозначается символом
называется скалярным квадратом вектора и обозначается символом  . Из формулы следует, что скалярный квадрат вектора равен квадрату его модуля:
. Из формулы следует, что скалярный квадрат вектора равен квадрату его модуля:  . Если векторы
. Если векторы 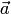 и
и  заданы своими координатами:
заданы своими координатами: 
 то их скалярное произведение может быть вычислено по формуле
то их скалярное произведение может быть вычислено по формуле 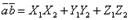 Отсюда следует необходимое и достаточное условие перпендикулярности двух векторов
Отсюда следует необходимое и достаточное условие перпендикулярности двух векторов  Угол
Угол  между векторами дается формулой
между векторами дается формулой 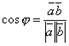 , или в координатах
, или в координатах  Косинус угла между векторами равен скалярному произведению векторов, поделенному на произведение модулей векторов.
Косинус угла между векторами равен скалярному произведению векторов, поделенному на произведение модулей векторов.
13. Н-мерный вектор. упорядоченная совокупность n действительных или комплексных чисел  называется n-мерным вектором. Числа
называется n-мерным вектором. Числа  называются координатами вектора. Суммой двух векторов
называются координатами вектора. Суммой двух векторов  и
и  называется вектор, координаты которого равны сумме соответствующих координат, то есть,
называется вектор, координаты которого равны сумме соответствующих координат, то есть,  складывать можно только векторы количество координат которых совпадает. Произведением действительного или комплексного числа
складывать можно только векторы количество координат которых совпадает. Произведением действительного или комплексного числа  и вектора
и вектора  называется вектор, координаты которого равны соответствующим координатам вектора а, умноженным на
называется вектор, координаты которого равны соответствующим координатам вектора а, умноженным на  то есть,
то есть, 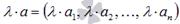
Линейная комбинация векторов Линейной комбинацией векторов e1,e2,..., ek линейного пространства L называется выражение С1·e1+С2·e2+...+Сk· ek. Числа С1, С2,..., Сk — коэффициенты линейной комбинации. Если все коэффициенты линейной комбинации С1·e1+С2·e2+...+Сk· ek равны нулю, то она называется тривиальной линейной комбинацией.Система e1,e2,..., ek линейно независима, если равенство С1·e1+С2·e2+...+Сk· ek = 0 возможно только для тривиальной линейной комбинации.Система e1,e2,..., ek линейно зависима, если существует нетривиальная линейная комбинация, для которой справедливо равенство С1·e1+С2·e2+...+Сk· ek = 0.
14.Векторное пространство.. Векторное пространство  называется n-мерным, если в нем можно найти n линейно независимых векторов, но больше, чем n линейно независимых векторов оно не содержит. Размерность пространства – это максимальное число содержащихся в нем линейно независимых векторов. Совокупность n линейно независимых векторов n- мерного векторного пространства
называется n-мерным, если в нем можно найти n линейно независимых векторов, но больше, чем n линейно независимых векторов оно не содержит. Размерность пространства – это максимальное число содержащихся в нем линейно независимых векторов. Совокупность n линейно независимых векторов n- мерного векторного пространства 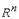 называется его базисом.
называется его базисом.
Теорема. Каждый вектор  линейного n- мерного пространства
линейного n- мерного пространства  можно представить, и притом единственным способом, в виде линейной комбинации векторов базиса. Доказательство. Пусть
можно представить, и притом единственным способом, в виде линейной комбинации векторов базиса. Доказательство. Пусть  - произвольный базис пространства
- произвольный базис пространства  и
и 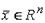 Так как любые n+1 векторов пространства
Так как любые n+1 векторов пространства  линейно зависимы, то зависимы, в частности, и векторы
линейно зависимы, то зависимы, в частности, и векторы  , т.е. существуют не равные одновременно нулю числа
, т.е. существуют не равные одновременно нулю числа  , такие, что
, такие, что  При этом
При этом  , в противном случае хотя бы одно из чисел
, в противном случае хотя бы одно из чисел  было бы отлично от нуля, и вектора
было бы отлично от нуля, и вектора  были бы линейно зависимы. Следовательно,
были бы линейно зависимы. Следовательно,  Полагая
Полагая  , будем иметь
, будем иметь 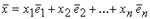 . Это представление
. Это представление 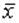 через
через  единственно. Доказывается от противного. Числа
единственно. Доказывается от противного. Числа  называются координатами вектора
называются координатами вектора  в базисе
в базисе  .
.
Теорема. Если  - линейно независимые векторы пространства
- линейно независимые векторы пространства  и любой вектор
и любой вектор  линейно выражается через
линейно выражается через  , то эти векторы образуют базис в
, то эти векторы образуют базис в  . Доказательство. Векторы
. Доказательство. Векторы  , по условию, линейно независимы. Покажем, что в пространстве
, по условию, линейно независимы. Покажем, что в пространстве  нет более чем n линейно независимых векторов. Выберем произвольные
нет более чем n линейно независимых векторов. Выберем произвольные 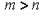 векторов из
векторов из 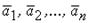 :. По условию, каждый из них можно линейно выразить через
:. По условию, каждый из них можно линейно выразить через  :
:  Рассмотрим матрицу:
Рассмотрим матрицу:  Так как число строк этой матрицы равно n, то ее ранг не больше, чем n, и значит, среди ее столбцов имеется не более, чем n линейно независимых. Но так как m>n, то m столбцов этой матрицы линейно зависимы. Следовательно, линейно зависимы и векторы
Так как число строк этой матрицы равно n, то ее ранг не больше, чем n, и значит, среди ее столбцов имеется не более, чем n линейно независимых. Но так как m>n, то m столбцов этой матрицы линейно зависимы. Следовательно, линейно зависимы и векторы  . Итак, пространство
. Итак, пространство  n – мерно и
n – мерно и  - его базис.
- его базис.
15.Скалярное произведение векторов в н мерном пространстве. Если каждой паре векторов x, y линейного пространства L поставлено в соответствие действительное число (x, y), так, что для любых x, y и z из L и любого действительного числа α справедливы следующие аксиомы:(x, y) = (y, x),(α·x, y) = α·(x, y),(x + y, z) =(x, z) + (y, z),(x, x)> 0 при x ≠ 0, (0, 0) = 0, то в пространстве L определено скалярное произведение (x, y).Если в линейном пространстве определено скалярное произведение, то такое пространство называется евклидовым пространством. Скалярным произведением векторов  и
и  в многомерном пространстве называется число
в многомерном пространстве называется число  Длиной n-мерного вектора
Длиной n-мерного вектора  называется квадратный корень из скалярного квадрата:
называется квадратный корень из скалярного квадрата:  Вектор, длина которого равна единице, называется единичным.
Вектор, длина которого равна единице, называется единичным.
16. Ортогональные векторы. Если скалярное произведение двух ненулевых векторов x и y евклидова пространства E равно нулю, то векторы называются ортогональными векторами:(x, y) ←→ x ⊥ y. Если длина вектора равна единице, он называется нормированным вектором:(x,x) = 1, |x| = 1.Если все векторы системы векторов нормированы, то система векторов называется нормированной системой.Если векторы системы векторов e1, e2,..., enпопарно ортогональны и нормированы, то система векторов называется ортонормированной системой: (ei, ej) = 0, если i ≠ j,(ei, ei) = 1. Если e1, e2,..., en — ортонормированная система и x = x1e1 + x2e2 +... + xnen — разложение вектора x по этой системе, то xi =(x, ei). Ортонормированная система, состоящая из n векторов n-мерного евклидова пространства, образует базис этого пространства. Такой базис называется ортонормированным базисом.Если e1, e2,..., en — ортонормированный базис n-мерного евклидова пространства и x = x1e1 + x2e2 +... + xnen — разложение вектора x по этому базису, то координаты xi вектора x в ортонормированном базисе вычисляются по формулам xi =(x, ei), i = 1, 2,..., n. Пусть e1, e2,..., en — ортонормированный базис n-мерного евклидова пространства и пусть x = x1e1 + x2e2 +... + xnen, y = y1e1 + y2e2 +... + ynen — разложения векторов x и y по этому базису.Тогда скалярное произведение векторов x и y вычисляется по формуле: (x, y) = x1· y1 + x2· y2 +... + xn· yn. Теорема. Во всяком n-мерном евклидовом пространстве Е существует ортонормированный базис. Доказательство. Согласно определению размерности в пространстве Е найдется n линейно независимых элементов f1, f2,..., fn. Докажем, что можно построить n элементов e1,e2,...,en, линейно выражающихся через f1, f2,..., fn и образующих ортонормированный базис. Проведем доказательство возможности построения таких элементов e1,e2,...,en методом математической индукции. Если имеется только один элемент f1, то для построения элемента e1 с нормой, равной единице, достаточно нормировать элемент f1, т.е. умножить этот элемент на число  , обратное его норме (напомним, что среди линейно независимых элементов f1, f2,..., fn не может быть нулевого элемента, так что норма f1 больше нуля). Мы получим при этом элемент e1 =
, обратное его норме (напомним, что среди линейно независимых элементов f1, f2,..., fn не может быть нулевого элемента, так что норма f1 больше нуля). Мы получим при этом элемент e1 =  f1 с нормой, равной единице.
f1 с нормой, равной единице.
Считая, что m — целое число, меньшее n, предположим, что нам удалось построить m элементов e1,e2,...,em, линейно выражающихся через f1, f2,..., fm, попарно ортогональных и имеющих нормы, равные единице. Докажем, что к этим элементам e1,e2,...,em можно присоединить еще один элемент em+1, линейно выражающийся через f1, f2,..., fm+1, ортогональный к каждому из элементов e1,e2,...,em и имеющий норму, равную единице. Убедимся в том, что этот элемент em+1 имеет вид em+1 = αm+1 [fm+1 - (fm+1,em),em - (fm+1,em-1),em-1 -... - (fm+1,e1)e1] где αm+1 — некоторое вещественное число. В самом деле, элемент em+1 линейно выражается через f1, f2,..., fm+1 (в силу того, что он линейно выражается через e1,e2,...,em, fm+1, акаждый из элементов e1,e2,...,em линейно выражается через f1, f2,..., fm). Отсюда сразу же следует, что при αm+1≠ 0 элемент em+1 заведомо не является нулевым (ибо, в противном случае, являлась бы нулевым элементом некоторая линейная комбинация линейно независимых элементов f1, f2,..., fm+1, в которой, в силу отличен от нуля коэффициент при fm+1). Далее из того, что элементы e1,e2,...,em попарно ортогональны и имеют нормы, равные единице, и из соотношения сразу же вытекает, что скалярное произведение (em+1, ek) равно нулю для любого номера k, равного 1, 2,..., m. Для завершения индукции остается доказать, что число αm+1 можно выбрать так, что норма элемента будет равна единице. Выше уже установлено, что при αm+1≠ 0 элемент em+1, а, стало быть, и элемент, заключенный в в квадратные скобки, не является нулевым. Стало быть, для того чтобы нормировать элемент, заключенный в квадратные скобки, следует взять число αm+1 обратным положительной норме этого, заключенного в квадратные скобки, элемента. При этом норма em+1 будет равна единице.Теорема доказана.
17. Определение оператора. Оператором называется правило, по которому каждому элементу x некоторого непустого множества X ставится в соответствие единственный элемент y некоторого непустого множества Y. Говорят, что оператор действует из X в Y.Действие оператора обозначают y = A(x), y — образ x, x — прообраз y.Если каждый элемнт y из Y имеет единственный прообраз x из X, y= A(x), оператор называют взаимно однозначным отображением X в Y или преобразованием X, X — область определения оператора. Пусть X и Y два линейные пространства. Оператор A, действующий из X в Y, называется линейным оператором, если для любых двух элементов u и v из X и любого числа α справедливо: A(u + v) = A(u) + A(v), A(α·u) = α· A(u).
18. Матрица линейного оператора. Линейный оператор A действует из n-мерного линейного пространства X в m-мерное линейное пространство Y. В этих пространствах определены базисы e = {e1,..., en} и f = {f1,..., fm}. Пусть A(ei) = a1i·f1 + a2i·f2 +...+ ami·fm — разложение образа i-го базисного вектора базиса e пространства X по базису f пространства Y, i = 1, 2,..., n. Матрицей линейного оператора в базисах e, f называется матрица A, столбцами которой являются координаты образов базисных векторов базиса e в базисе f, A = {aij}= {A(ej)i}:  Координаты образа y = A(x) и прообраза x связаны соотношеннием: y = A· x,
Координаты образа y = A(x) и прообраза x связаны соотношеннием: y = A· x, 

Определение. Суммой операторов A и B называется оператор, определенный в Rn на  и действующий следующим образом:
и действующий следующим образом:  .Определение. Произведением оператора A на число
.Определение. Произведением оператора A на число  называется оператор, определенный в Rn на
называется оператор, определенный в Rn на  и действующий следующим образом:
и действующий следующим образом: 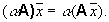 Определение. Произведением AB операторов A и B называется оператор, определенный в Rn на
Определение. Произведением AB операторов A и B называется оператор, определенный в Rn на  и действующий следующим образом:
и действующий следующим образом: 
Пример:Линейные операторы A и B действуют в 3-х мерном линейном пространстве X = {x| x = (x1, x2, x3)} следующим образом: A(x) = (2x1, x2 + 5x3, − x1), B(x) = (x1− x2, x3 + x2, 0) для всех x из X.Матрицы операторов A и B имеют соответственно вид: 

19.Собственные векторы и собственные значения оператора. Определение. Ненулевой вектор x называется собственным вектором линейного оператора 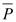 , если найдется такое число λ, называемое собственным значением линейного оператора, что
, если найдется такое число λ, называемое собственным значением линейного оператора, что  (x) = λ·x (1) Рассмотрим линейный оператор A, действующий в линейном пространстве X: y = A(x), ∀x ∈ X, y ∈ X. Число λ называется собственным значением оператора A, если существует такой ненулевой вектор x, что справедливо равенство A(x) = λ·x. Любой ненулевой вектор x ≠0, удовлетворяющий этому уравнению, называется собственным вектором оператора A, отвечающим собственному значению λ. A(x) = λ·x, x ≠0, x ∈ X. Пусть A — линейный оператор, действующий в n-мерном линейном пространстве X, λ i— собственное значение оператора A, а ei — соответствующий собственный вектор: A(ei) = λ iei, ei ≠ 0, ei ∈X.Или пусть A — матрица оператора A, или произвольная квадратноя матрица, λ i— собственное значение матрицы A, а ei — соответствующий собственный вектор: A·ei = λ iei,ei ≠ 0, ei ∈X. — Если λ1, λ2,..., λn — собственные значения матрицы A, то tr A = a11+ a22+...+ ann = λ1 + λ2 +...+ λn. — Если λ1, λ2,..., λn — собственные значения матрицы A, то det A = λ1 · λ2 ·...· λn. — Собственные значения λ i являются корнями характеристического уравнения det(A −λE) = 0. — Оператор A (матрица A) имеет не более n различных собственных значений. — Собственные значения матриц A и AT совпадают. — Если матрица A обратима, то все её собственные значения отличны от нуля, λ i≠ 0; при этом собственными значениями обратной матрицы A− 1 являются числа (λ i)− 1, а соответствующие собственные векторы совпадают. — Если число λ — собственное значение матрицы A, то собственным значением матрицы Ak является число λk, а соответствующие собственные векторы совпадают. — Собственные значения подобных матриц A и C− 1·A·C совпадают. Здесь C — невырожденная матрица. — Собственный вектор, отвечающий собственному значению λ i является ненулевым решением линейной однородной системы (A −λE)· x = 0, x≠ 0, x ∈ X. — Собственные векторы, отвечающие различным собственным значениям, линейно независимы. — Если линейный оператор A имеет n различных собственных значений, то соответствующие собственные векторы образуют базис пространства X, который называется собственным базисом линейного оператора. — Если линейный оператор имеет собственный базис, то матрица оператора в собственном базисе имеет диагональный вид; диагональными элементами являются собственные значения оператора. — Собственные векторы, отвечающие различным собственным значениям, ортогональны. Пусть A — линейный оператор, действующий в n-мерном линейном пространстве X, λ i— собственное значение оператора A, а ei — соответствующий собственный вектор: A(ei) = λ iei, ei ≠ 0, ei ∈X. Или пусть A — матрица оператора A, или произвольная квадратноя матрица, λ i— собственное значение матрицы A, а ei — соответствующий собственный вектор: A·ei = λ iei,ei ≠ 0, ei ∈X. Собственные значения λ i являются корнями характеристического уравнения det(A −λE) = 0.Многочлен P(λ) = − det(A − λE), из левой части характеристического уравнения, называется характеристическим многочленом матрицы A. Характеристический многочлен P(λ) = − det(A − λE) — многочлен степени n относительно λ:P(λ) = λn − an-1λn-1+ an-2λn-2+...+ (−1)na0.
(x) = λ·x (1) Рассмотрим линейный оператор A, действующий в линейном пространстве X: y = A(x), ∀x ∈ X, y ∈ X. Число λ называется собственным значением оператора A, если существует такой ненулевой вектор x, что справедливо равенство A(x) = λ·x. Любой ненулевой вектор x ≠0, удовлетворяющий этому уравнению, называется собственным вектором оператора A, отвечающим собственному значению λ. A(x) = λ·x, x ≠0, x ∈ X. Пусть A — линейный оператор, действующий в n-мерном линейном пространстве X, λ i— собственное значение оператора A, а ei — соответствующий собственный вектор: A(ei) = λ iei, ei ≠ 0, ei ∈X.Или пусть A — матрица оператора A, или произвольная квадратноя матрица, λ i— собственное значение матрицы A, а ei — соответствующий собственный вектор: A·ei = λ iei,ei ≠ 0, ei ∈X. — Если λ1, λ2,..., λn — собственные значения матрицы A, то tr A = a11+ a22+...+ ann = λ1 + λ2 +...+ λn. — Если λ1, λ2,..., λn — собственные значения матрицы A, то det A = λ1 · λ2 ·...· λn. — Собственные значения λ i являются корнями характеристического уравнения det(A −λE) = 0. — Оператор A (матрица A) имеет не более n различных собственных значений. — Собственные значения матриц A и AT совпадают. — Если матрица A обратима, то все её собственные значения отличны от нуля, λ i≠ 0; при этом собственными значениями обратной матрицы A− 1 являются числа (λ i)− 1, а соответствующие собственные векторы совпадают. — Если число λ — собственное значение матрицы A, то собственным значением матрицы Ak является число λk, а соответствующие собственные векторы совпадают. — Собственные значения подобных матриц A и C− 1·A·C совпадают. Здесь C — невырожденная матрица. — Собственный вектор, отвечающий собственному значению λ i является ненулевым решением линейной однородной системы (A −λE)· x = 0, x≠ 0, x ∈ X. — Собственные векторы, отвечающие различным собственным значениям, линейно независимы. — Если линейный оператор A имеет n различных собственных значений, то соответствующие собственные векторы образуют базис пространства X, который называется собственным базисом линейного оператора. — Если линейный оператор имеет собственный базис, то матрица оператора в собственном базисе имеет диагональный вид; диагональными элементами являются собственные значения оператора. — Собственные векторы, отвечающие различным собственным значениям, ортогональны. Пусть A — линейный оператор, действующий в n-мерном линейном пространстве X, λ i— собственное значение оператора A, а ei — соответствующий собственный вектор: A(ei) = λ iei, ei ≠ 0, ei ∈X. Или пусть A — матрица оператора A, или произвольная квадратноя матрица, λ i— собственное значение матрицы A, а ei — соответствующий собственный вектор: A·ei = λ iei,ei ≠ 0, ei ∈X. Собственные значения λ i являются корнями характеристического уравнения det(A −λE) = 0.Многочлен P(λ) = − det(A − λE), из левой части характеристического уравнения, называется характеристическим многочленом матрицы A. Характеристический многочлен P(λ) = − det(A − λE) — многочлен степени n относительно λ:P(λ) = λn − an-1λn-1+ an-2λn-2+...+ (−1)na0.
20.Матрица линейного оператора. Линейный оператор A действует из n-мерного линейного пространства X в m-мерное линейное пространство Y. В этих пространствах определены базисы e = {e1,..., en} и f = {f1,..., fm}. Пусть A(ei) = a1i·f1 + a2i·f2 +...+ ami·fm — разложение образа i-го базисного вектора базиса e пространства X по базису f пространства Y, i = 1, 2,..., n. Матрицей линейного оператора в базисах e, f называется матрица A, столбцами которой являются координаты образов базисных векторов базиса e в базисе f, A = {aij}= {A(ej)i}:  Координаты образа y = A(x) и прообраза x связаны соотношеннием: y = A· x,
Координаты образа y = A(x) и прообраза x связаны соотношеннием: y = A· x, 

Определение. Суммой операторов A и B называется оператор, определенный в Rn на  и действующий следующим образом:
и действующий следующим образом:  .Определение. Произведением оператора A на число
.Определение. Произведением оператора A на число  называется оператор, определенный в Rn на
называется оператор, определенный в Rn на  и действующий следующим образом:
и действующий следующим образом: 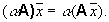 Определение. Произведением AB операторов A и B называется оператор, определенный в Rn на
Определение. Произведением AB операторов A и B называется оператор, определенный в Rn на  и действующий следующим образом:
и действующий следующим образом: 
Пример:Линейные операторы A и B действуют в 3-х мерном линейном пространстве X = {x| x = (x1, x2, x3)} следующим образом: A(x) = (2x1, x2 + 5x3, − x1), B(x) = (x1− x2, x3 + x2, 0) для всех x из X.Матрицы операторов A и B имеют соответственно вид: 

21. Квадратичная форма Определение квадратичной формы Квадратичная форма переменных  - функция
- функция 
 коэффициенты квадратичной формы. Без ограничения общности считают
коэффициенты квадратичной формы. Без ограничения общности считают 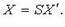 тогда
тогда 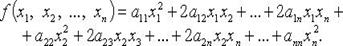 Если переменные
Если переменные  принимают действительные значения и
принимают действительные значения и  квадратичная форма называется действительной. Матричная запись квадратичной формы Матрица
квадратичная форма называется действительной. Матричная запись квадратичной формы Матрица  называется матрицей квадратичной формы, ее ранг - рангом квадратичной формы. Квадратичная форма называется невырожденной, если
называется матрицей квадратичной формы, ее ранг - рангом квадратичной формы. Квадратичная форма называется невырожденной, если  Главные миноры матрицы A называются главными минорами квадратичной формы.Пример Пусть k(x) = x12 + x22— квадратичная форма в пространствеR2.Пусть e1= (1, 0), e2= (0, 1) — базис в R2. Вычислим матрицу A квадратичной формы.Поскольку симметричная билинейная форма φ(x, y) = (x, y) — полярная для квадратичной формы k(x) = φ(x, x) то матрица A квадратичной формы совпадает с матрицей Φ билинейной формы φ(x, y):
Главные миноры матрицы A называются главными минорами квадратичной формы.Пример Пусть k(x) = x12 + x22— квадратичная форма в пространствеR2.Пусть e1= (1, 0), e2= (0, 1) — базис в R2. Вычислим матрицу A квадратичной формы.Поскольку симметричная билинейная форма φ(x, y) = (x, y) — полярная для квадратичной формы k(x) = φ(x, x) то матрица A квадратичной формы совпадает с матрицей Φ билинейной формы φ(x, y): 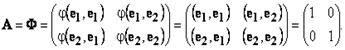 Проверим. Для этого подставим матрицу A в матричное представление квадратичной формы k(x)=xT·A·x:
Проверим. Для этого подставим матрицу A в матричное представление квадратичной формы k(x)=xT·A·x:  Матрица квадратичной формы вычислена верно
Матрица квадратичной формы вычислена верно
22. Квадратичная форма (канонический вид). Приведение квадратичной формы к каноническому виду. Пример. Закон инерции квадратичных форм.
Квадратичная форма называется канонической, если все  т. е.
т. е.

Теорема: Любая квадратичная форма с помощью невырожденного линейного преобразования переменных может быть приведена к каноническому виду.
Для приведения квадратичной формы к каноническому виду необходимо произвести такие преобразования, что бы матрица квадратичной формы стала диагональной.
Условия приведения квадратной матрицы к диагональному виду:
Если квадратная матрицы порядка п имеет несколько линейно независимых собственных векторов и соответствующих собственных значений, то она может быть приведена к диагональному виду, причём элементы диагональной матрицы являются собственные значения.

Теорема (закон инерции квадратичных форм) Число слагаемых с положительным (отрицательным)коэффициентом квадратичной формы не зависит от способа приведения формы к этому виду. Например, квадратичную форму L
23. Положительно и отрицательно определенная, знакоопределенная квадратичные формы. Критерии знакоопределенности квадратичной формы (через собственные значения ее матрицы и по критерию Сильвестра).
Квадратичная форма L(x1,x2,….,xn) называется положительно (отрицательно) определенной, если при всех значениях переменных,из которых хотя бы одно отлично от нуля
L(x1,x2,….,xn)>0 (L(x1,x2,….,xn)<0)
Квадратичная форма L=X’AX положительно определена тогда и только тогда, если:
а)все собственные значения ƛi матрицы А положительна
б)все главные (угловые) минора матрицы А положительны(по Сильвестору)
Квадратичная форма L=X’AX отрицательно определена тогда и только тогда, если:
а)все собственные значения ƛi матрицы А отрицательны
б)все главные (угловые) минора матрицы А нечетного порядка отрицательны. А матрицы четного порядка положительны(по Сильвестору)
Если квадратичная форма знакоопределенная, то все главные (угловые) миноры ее матрицы отличны от нуля
Критерий собственных значений матрицы:
· Если все собственные значения больше нуля, то квадратичная форма тоже больше нуля.
· Если все собственные значения меньше нуля, то квадратичная форма тоже меньше нуля.
· Если все собственные значения больше, либо равны нулю, то квадратичная форма тоже меньше нуля.
· Если некоторые собственные значения равны нулю, а остальные меньше, то квадратичная форма отрицательно полу определена.
· Если некоторые собственные значения больше нуля, а остальные меньше, то квадратичная форма может иметь любой знак.
Критерий Сильвестра:
Критерий Сильвестра позволяет выделить положительную и отрицательную знакоопределённость квадратичной формы с помощью вычисления нескольких определителей, являющихся угловыми минорами квадратичной формы.
После вычисления миноров суждение о знакоопределенности квадратичной формы выносится по следующему правилу:
· Если все угловые миноры положительны, то квадратичная форма положительно определена.
· Если угловые миноры чередуются знаком, начиная с минуса, то есть: 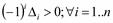 ,то квадратичная форма отрицательно определена.
,то квадратичная форма отрицательно определена.
· Если идёт чередование знаков, начиная с плюса, или любое другое сочетание знаков, или существуют миноры, равные нулю (последний минор не равен нулю), то форма знака неопределенна.
· Если последний минор равен нулю, в этом случае критерий Сильвестра не различает знакоопределённости формы, и необходимо использовать другой критерий.
24. Уравнение линии на плоскости. Точка пересечения двух линий. Основные виды уравнений прямой на плоскости (одно из них вывести).
Уравнением линии на плоскости Oxy называется уравнение, которому удовлетворяют координаты x и y каждой точки данной линии и не удовлетворяют координаты любой точки, не лежащей на этой линии. Пусть даны две прямые А1х+В1у+С1=0 и А2х+В2у+С2=0. Очевидно, координаты их точки пересечения должны удовлетворять уравнению каждой прямой, т е они могут быть найдены из системы: { А1х+В1у+С1=0; А2х+В2у+С2=0}. Если прямые не параллельны, т е А1/А2≠В1/В2, то решение системы дает ед точку пересечения прямых.
25. Общее уравнение прямой на плоскости, его исследование. Условия параллельности и перпендикулярности прямых.
а) Запишем ур-ние прямой с к=1: у=kх+b; -kx+y-b=0; -kx→Ax,y→By.-b→C;Ax+By+C=0-ур-ние прямой. Частные случай ур-ния Ах+Ву+С=0: 1) А=0,следов. Ву+С=0, В,С-const.у=-С/В. Прямая || оси ОХ. А=С=0,следов. у=0-прямая совпадает с осью ОХ.
2) В=0,следов. Ах+С=0, А,С- const. Х=-С/А. А≠0. Прямая || оси ОУ. В=С=0,следов. х=0- прямая совпадает с осью ОУ.
3) С=0, следов. Ах+Ву=0. у=-А/В×х-прямая проходит ч/з начало координат.
б) 1. Если прямая L1|| L2,следов. φ =0, tg φ=0, следов. k1=k2- условие || двух прямых.
2. L1┴ L2, тогда φ =π/2, следов. tg π/2-неопределен. сtg π/2=0, следов. сtgφ=1/tgφ=(1+k1k2)/(k2- k1). сtgφ=0, следов. 1+k1k2=0, k1k2= -1-условие ┴ двух прямых.
26. Кривые второго порядка, их общее уравнение. Нормальное уравнение окружности. Каноническое уравнение эллипса. Геометрический смысл параметров окружности и эллипса.
Кривой второго порядка называется алгебраическая линия второй степени, общее уравнение которой имеет следующий вид:  Любые уравнения такого вида можно привести к каноническому виду.
Любые уравнения такого вида можно привести к каноническому виду.
Окружность – множество всех точек плоскости, равноудаленных от заданной точки, называемой центром.
 Нормальные уравнения окружности радиуса R с центром в точках О’(x0;y0) и O (0;0) соответственно имеют вид
Нормальные уравнения окружности радиуса R с центром в точках О’(x0;y0) и O (0;0) соответственно имеют вид
(x – x 0)2 + (y – y 0)2 = R2,
X2 + y2 = R 2.
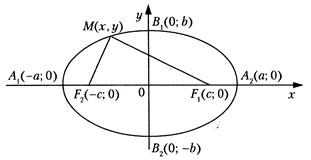
Эллипс – множество всех точек плоскости, для каждой из которых сумма расстояний до двух заданных фиксированных точек, называемых фокусами, есть величина постоянная.
Каноническое уравнение эллипса имеет вид x2/a2+y2/b2=1,
где a и b – полуоси эллипса; F 1(c;0) и F 2 (- c;0) – фокусы эллипса, если a > b.
При этом C 2 = a 2 – b 2.
Эксцентриситет эллипса e характеризует форму эллипса: e = c/a<1
27. Канонические уравнения гиперболы и параболы. Геометрический смысл их параметров. Уравнение асимптот гиперболы. График обратно-пропорциональной зависимости и квадратного трехчлена.
 Гипербола – множество всех точек плоскости, для каждой из которых модуль разности расстояний до двух заданных фиксированных точек, называется фокусами, есть величина постоянная.
Гипербола – множество всех точек плоскости, для каждой из которых модуль разности расстояний до двух заданных фиксированных точек, называется фокусами, есть величина постоянная.
Каноническое уравнение гиперболы имеет вид x2/a2-y2/b2=1
где a и b – соответственно действительная
и мнимая полуоси гиперболы; F 1(c;0) и
F 2 (- c;0) – фокусы гиперболы (c > a).
При этом C 2 = a 2 + b 2
Эксцентриситет гиперболы e = c/a >1
Уравнения асимптот гиперболы: y= ± bx/ a.

Парабола – множество всех точек плоскости, равноудаленных от заданной
точки, называемой фокусом, и заданной прямой, называемой директрисой.
Каноническое уравнение параболы с вершиной в начале координат имеет вид
y 2 = 2 px (симметрична относительно оси Ox)
или
x 2 = 2 py (симметрична относительно оси Oy)
Уравнение директрисы параболы x = -p/2
28. Общее уравнение плоскости в пространстве и его частные случаи. Нормальный вектор плоскости. Условия параллельности и перпендикулярности двух плоскостей.
Общее уравнение плоскости (рис. 4.13)

где  - нормальный вектор плоскости.
- нормальный вектор плоскости.
 В векторном виде
В векторном виде  .
.
Частные случаи общего уравнения плоскости:
1) By + Cz + D = 0 - параллельна оси Ox;
2) Ax + Cz + D = 0 - параллельна оси Oy;
3) Ax + By + D = 0 - параллельна оси Oz;
4) Cz + D = 0 - параллельна оси Oxy;
5) By + D = 0 - параллельна оси Oxz;
6) Ax + D = 0 - параллельна оси Oyz;
7) Ax + By + Cz = 0 - проходит через начало координат;
8) By + Cz = 0 - проходит через ось Ox;
9) Ax + Cz = 0 - проходит через ось Oy;
10) Ax + By = 0 - проходит через ось Oz;
11) z = 0 - плоскость Oxy;
12) y = 0 - плоскость Oxz;
13) x = 0 - плоскость Oyz.
Необходимое и достаточное условие перпендикулярности двух плоскостей
 или
или 
Условием параллельности двух плоскостей является пропорциональность коэффициентов при одноименных переменных: А1/А2=В1/В2=С1/С2
29. Уравнения прямой линии в пространстве как линии пересечения двух плоскостей. Канонические уравнения прямой. Направляющий вектор прямой. Условия параллельности и перпендикулярности двух прямых в пространстве.
Определение: Общими уравнениями прямой в пространстве называется система:

Канонические уравнения прямой в пространстве.
Рассмотрим  , проходящую через (.)
, проходящую через (.)  параллельно вектору
параллельно вектору 


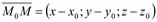
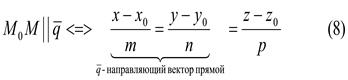
(8)- канонические уравнения прямых в пространстве.
Замечание: если одна или две координаты вектора  нулевые, не следует понимать отношение (8) как деление на ноль, если какая-то из координат вектора
нулевые, не следует понимать отношение (8) как деление на ноль, если какая-то из координат вектора  равна 0 => прямая лежит в одной из координатных плоскостей.
равна 0 => прямая лежит в одной из координатных плоскостей.

Пример:

Из канонических уравнений прямой легко можно получить общие уравнения.

30. Углы между двумя плоскостями, двумя прямыми, между прямой и плоскостью. Условия их параллельности и перпендикулярности.
Угол между плоскостями. Даны две плоскости A1x+B1y+C1z+D1=0 (1) и A2x+B2y+C2z+D2=0 (2)

Необходимое и достаточное условие перпендикулярности двух плоскостей
 или
или  Условием параллельности двух плоскостей является пропорциональность коэффициентов при одноименных переменных: А1/А2=В1/В2=С1/С2 Угол между прямыми:
Условием параллельности двух плоскостей является пропорциональность коэффициентов при одноименных переменных: А1/А2=В1/В2=С1/С2 Угол между прямыми: 
Условие параллельности двух прямых: А1/А2=В1/В2=С1/С2 Условие перпендикулярности двух прямых в пространстве 
Угол между прямой и плоскостью: Углом между прямой и плоскостью называется любой смежный угол, образованный самой прямой и проекцией этой прямой на плоскости:
 Условие параллельности прямой и плоскости: Am+Bn+Cp=0 Условие перпендикулярности прямой и плоскости:A/m=B/n=C/p
Условие параллельности прямой и плоскости: Am+Bn+Cp=0 Условие перпендикулярности прямой и плоскости:A/m=B/n=C/p






