Б) посредством z-преобразования.
а ) прямым способом: находим ошибкукоэффициента корреляции при малых п по формуле:
Sr = √ 1 – 0,14 / √ 16 = √ 0,86 / 4 = 0,93 / 4 = 0,23
Определяем достоверность связи:
tф = r / Sr = 0,37 / 0,23 = 1,61
Делаем статистическое заключение:
tф (1,61) < tт (2,92) Нулевая гипотеза сохраняется
(Связь не доказана при p<1% и df = n – 2 = 16)
б) посредством z-преобразования:
Находим число z, соответствующее коэффициенту корреляции 0,37:
z (r = 0,37) = 0,39
Вычисляем ошибку числа z:
Sz = 1 / √ 15 = 1 / 3,87 = 0,26
Определяем достоверность связи:
tф = z / Sz = 0,39 / 0,26 = 1,5
Делаем статистическое заключение:
tф (1,5) < tт (2,90) Нулевая гипотеза сохраняется
(Связь не доказана при p<1% и df = n – 2 = 16
2). r = 0,87 n = 27 p<0,1%
Определите доверительный интервал для коэффициента корреляции генеральной совокупности (ρ) а) прямым способом; б) посредством z-преобразования.
а) прямым способом:
находим ошибкукоэффициента корреляции при малых п по формуле:
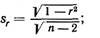Sr = √ 1 – 0,76 / √ 25 = √ 0,24 / 5 = 0,49 / 5 = 0,1
Определяем доверительный интервал для коэффициента корреляции генеральной совокупности (ρ):
tт = 3,73
r- tт* Sr < ρ < r+ tт* Sr 0,87-3,73*0,1< ρ <0,87+3,73*0,1
0,87-0,37< ρ <0,87+0,37 0,40< ρ <1,24 0,4 < ρ <1,0
б) посредством z-преобразования:
Находим число z, соответствующее коэффициенту корреляции 0,87:
z (r = 0,87) = 1,333
Вычисляем ошибку числа z:
Sz = 1 / √ 24 = 1 / 4,9 = 0,20
Вычисляем доверительный интервал для коэффициента корреляции генеральной совокупности (ρ) в условных единицах z
z- tт* Sz < ρ < z+ tт* Sz 1.333-3,73*0,2< ρ <1.333+3,73*0,2
1.333-0,75< ρ <1.333+0,75 0,583< ρ <2,083
Производим обратное преобразование значений числа z в r:
z = 0,583 = r = 0,53; z = 2,083 = r = 0,97
0,53< ρ <0,97 при p<0,1% и df = n – 2 = 25
3. r1 = 0,36. r2 = 0,75 n1 = 27 n2 = 27 p<1%
Определите достоверность разницы между коэффициентами корреляции
А) прямым способом б) посредством z-преобразования
а) прямым способом:
находим ошибкукоэффициентов корреляции при малых п по формуле:
Sr1 = √ 1 – 0,362 / √ 25 = √1 - 0,13 / 5 = 0,87 / 5 = 0,17
Sr2 = √ 1 – 0,752 / √ 25 = √1 - 0,56 / 5 = 0,44 / 5 = 0,09
Вычисляем достоверность различий между коэффициентами корреляции:
tф =| r1 - r2| / √ Sr12 + Sr22 = | 0,36 – 0,75| / √ 0,17 + 0,09 = 0,39 / √ 0,26 = 0,39 / 0,5 = 0,78
Определяем достоверность различий:
tф (0,78) < tт (2,58) Нулевая гипотеза сохраняется
(Связь не доказана при p<1% и df = n1 + n2 – 2 = 27 + 27 – 2 = 52
б) посредством z-преобразования:
Находим число z, соответствующее коэффициенту корреляции 0,36:
z (r = 0,36) = 0,36
Вычисляем ошибку числа z:
Sz = 1 / √ 27-3 = 1 / 24 = 1 / 4,9 = 0,2
Находим число z, соответствующее коэффициенту корреляции 0,75
z (r = 0,75) = 0,97
Вычисляем ошибку числа z:
Sz = 1 / √ 27-3 = 1 / 24 = 1 / 4,9 = 0,2
Определяем достоверность различий:
tф =| z1 - z2 | / √ Sz12 + Sz22 = | 0,38 – 0,97 | / √ 0,22 + 0,22 = 0,59 / √ 0,08 = 0,59 / 0,28 = 2,10
tф (2,10) < tт (2,58) Нулевая гипотеза сохраняется
(Связь не доказана при p<1% и df = n1 + n2 – 2 = 27 + 27 – 2 = 52
4. р = 18% n = 36 Определите доверительный интервал для доли генеральной совокупности Ро при р< 0,01 а) прямым способом; б) посредством φ-преобразования.
а) прямым способом:
Определяем ошибку доли по формуле 
Sp = √ 0,18*0,82 / 36 = √ 0,15 / 36 = √0,004 = 0,065 = 6,5%
Находим доверительный интервал по формуле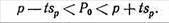 
18 – 2,58*6,5<Ро<18 + 2,58*6,5 18 – 16,8<Ро<18 + 16,8
1,2%<Ро<34,8%
б) посредством φ -преобразования:
φ (18%) = 0,876; Определяем ошибку доли по формуле S φ = 1 / n
S φ = 1 / √ 36 = 1 / 6 = 0,17 Находим доверительный интервал:
φ – t * S φ < φо < φ + t * S φ 0,876 – 2,58*0,17<φо<0,876+2,58*0,17
0,876 – 0,439<φо<0,876 + 0,439 0,437< φо <1,315
Производим обратное преобразование значений числа φ в проценты:
φ = 0,437 = 4,7% φ = 1,315 = 37,3%
4,7%<Ро<37,3%
5. р1= 18% n1 = 36 р2= 58% n2 = 36
Определите достоверность разницы между двумя выборочными долями при р<0,05
