Если между экономическими явлениями существуют нелинейные соотношения, то они выражаются с помощью соответствующих нелинейных функций.
Различают два класса нелинейных регрессий:
1. Регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам, например
– полиномы различных степеней – 
, 
;
– равносторонняя гипербола – 
;
– полулогарифмическая функция – 
.
2. Регрессии, нелинейные по оцениваемым параметрам, например
– степенная – 
;
– показательная – 
;
– экспоненциальная – 
.
Регрессии нелинейные по включенным переменным приводятся к линейному виду простой заменой переменных, а дальнейшая оценка параметров производится с помощью метода наименьших квадратов. Рассмотрим некоторые функции.
Парабола второй степени приводится к линейному виду с помощью замены: 
. В результате приходим к двухфакторному уравнению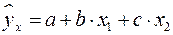 
, оценка параметров которого при помощи МНК, как будет показано в параграфе 2.2 приводит к системе следующих нормальных уравнений:
А после обратной замены переменных получим
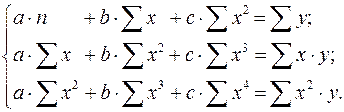(1.17)
Парабола второй степени обычно применяется в случаях, когда для определенного интервала значений фактора меняется характер связи рассматриваемых признаков: прямая связь меняется на обратную или обратная на прямую.
Равносторонняя гипербола может быть использована для характеристики связи удельных расходов сырья, материалов, топлива от объема выпускаемой продукции, времени обращения товаров от величины товарооборота, процента прироста заработной платы от уровня безработицы (например, кривая А.В. Филлипса), расходов на непродовольственные товары от доходов или общей суммы расходов (например, кривые Э. Энгеля) и в других случаях. Гипербола приводится к линейному уравнению простой заменой: 
. Система линейных уравнений при применении МНК будет выглядеть следующим образом:
(1.18)
Аналогичным образом приводятся к линейному виду зависимости , 
и другие.
Несколько иначе обстоит дело с регрессиями нелинейными по оцениваемым параметрам, которые делятся на два типа: нелинейные модели внутренне линейные (приводятся к линейному виду с помощью соответствующих преобразований, например, логарифмированием) и нелинейные модели внутренне нелинейные (к линейному виду не приводятся).
К внутренне линейным моделям относятся, например, степенная функция – , показательная – , экспоненциальная – , логистическая – 
, обратная – 
.
К внутренне нелинейным моделям можно, например, отнести следующие модели: 
, 
.
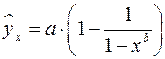Среди нелинейных моделей наиболее часто используется степенная функция 
, которая приводится к линейному виду логарифмированием:
;
;
,
где 
. Т.е. МНК мы применяем для преобразованных данных:
а затем потенцированием находим искомое уравнение.
Широкое использование степенной функции связано с тем, что параметр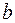 
в ней имеет четкое экономическое истолкование – он является коэффициентом эластичности. (Коэффициент эластичности показывает, на сколько процентов измениться в среднем результат, если фактор изменится на 1%.) Формула для расчета коэффициента эластичности имеет вид:
. (1.19)
Так как для остальных функций коэффициент эластичности не является постоянной величиной, а зависит от соответствующего значения фактора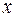 
, то обычно рассчитывается средний коэффициент эластичности:
. (1.20)
Приведем формулы для расчета средних коэффициентов эластичности для наиболее часто используемых типов уравнений регрессии:
Таблица 1.5
Вид функции, 
| Первая производная, 
| Средний коэффициент эластичности, 
|
|
| 
|
| 
| 
|
| 
| 
|
|
| 
|
|
| 
| 
|
| 
| 
|
| 
| 
|
| 
| 
|
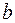
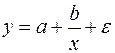
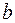
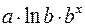
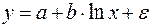
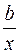
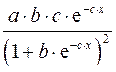
Возможны случаи, когда расчет коэффициента эластичности не имеет смысла. Это происходит тогда, когда для рассматриваемых признаков бессмысленно определение изменения в процентах.
Уравнение нелинейной регрессии, так же, как и в случае линейной зависимости, дополняется показателем тесноты связи. В данном случае это индекс корреляции:
, (1.21)
где 
– общая дисперсия результативного признака , 
– остаточная дисперсия.
Величина данного показателя находится в пределах: 
. Чем ближе значение индекса корреляции к единице, тем теснее связь рассматриваемых признаков, тем более надежно уравнение регрессии.
Квадрат индекса корреляции носит название индекса детерминации и характеризует долю дисперсии результативного признака , объясняемую регрессией, в общей дисперсии результативного признака:
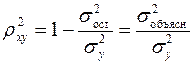, (1.22)
т.е. имеет тот же смысл, что и в линейной регрессии;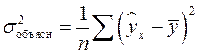 
.
Индекс детерминации 
можно сравнивать с коэффициентом детерминации 
для обоснования возможности применения линейной функции. Чем больше кривизна линии регрессии, тем величина меньше . А близость этих показателей указывает на то, что нет необходимости усложнять форму уравнения регрессии и можно использовать линейную функцию.
Индекс детерминации используется для проверки существенности в целом уравнения регрессии по 
-критерию Фишера:
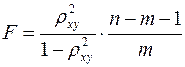, (1.23)
где – индекс детерминации, 
– число наблюдений,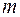 
– число параметров при переменной 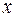. Фактическое значение -критерия (1.23) сравнивается с табличным при уровне значимости 
и числе степеней свободы 
(для остаточной суммы квадратов) и 
(для факторной суммы квадратов).
О качестве нелинейного уравнения регрессии можно также судить и по средней ошибке аппроксимации, которая, так же как и в линейном случае, вычисляется по формуле (1.8).
Рассмотрим пример из параграфа 1.1, предположив, что связь между признаками носит нелинейный характер, и найдем параметры следующих нелинейных уравнени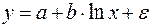й: , 
и .
Для нахождения параметров регрессии делаем замену 
и составляем вспомогательную таблицу (
).
Таблица 1.5
| 
| 
| 
| 
| 
| 
| 
| 
| 
| |
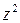
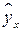
| 1,2 | 0,182 | 0,9 | 0,164 | 0,033 | 0,81 | 0,499 | 0,401 | 0,1610 | 44,58 | |
| 3,1 | 1,131 | 1,2 | 1,358 | 1,280 | 1,44 | 1,508 | -0,308 | 0,0947 | 25,64 | |
| 5,3 | 1,668 | 1,8 | 3,002 | 2,781 | 3,24 | 2,078 | -0,278 | 0,0772 | 15,43 | |
| 7,4 | 2,001 | 2,2 | 4,403 | 4,006 | 4,84 | 2,433 | -0,233 | 0,0541 | 10,57 | |
| 9,6 | 2,262 | 2,6 | 5,881 | 5,116 | 6,76 | 2,709 | -0,109 | 0,0119 | 4,20 | |
| 11,8 | 2,468 | 2,9 | 7,157 | 6,092 | 8,41 | 2,929 | -0,029 | 0,0008 | 0,99 | |
| 14,5 | 2,674 | 3,3 | 8,825 | 7,151 | 10,89 | 3,148 | 0,152 | 0,0232 | 4,62 | |
| 18,7 | 2,929 | 3,8 | 11,128 | 8,576 | 14,44 | 3,418 | 0,382 | 0,1459 | 10,05 | |
| Итого | 71,6 | 15,315 | 18,7 | 41,918 | 35,035 | 50,83 | 18,720 | -0,020 | 0,5688 | 116,08 |
| Среднее значение | 8,95 | 1,914 | 2,34 | 5,240 | 4,379 | 6,35 | – | – | 0,0711 | 14,51 |
| – | 0,846 | 0,935 | – | – | – | – | – | – | – |
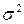
| – | 0,716 | 0,874 | – | – | – | – | – | – | – |
Найдем уравнение регрессии:
,
.
Т.е. получаем следующее уравнение регрессии: 
. Теперь заполняем столбцы 8-11 нашей таблицы.
Индекс корреляции находим по формуле (1.21):
,
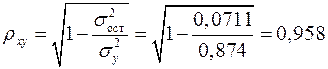а индекс детерминации 
, который показывает, что 91,8% вариации результативного признака объясняется вариацией признака-фактора, а 8,2% приходится на долю прочих факторов.
Средняя ошибка аппроксимации: 
, что недопустимо велико.
-критерий Фишера:
,
значительно превышает табличное 
.
Изобразим на графике исходные данные и линию регрессии:
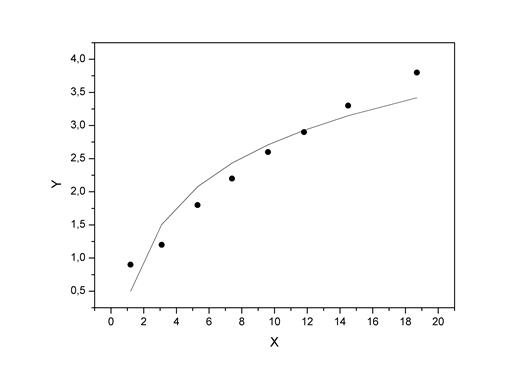
Рис. 1.6.
Для нахождения параметров регрессии делаем замену 
и составляем вспомогательную таблицу ().
Таблица 1.6
|
|
|
|
|
|
|
|
|
|
| |
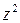
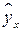
| 1,2 | 1,10 | 0,9 | 0,99 | 1,2 | 0,81 | 0,734 | 0,166 | 0,0276 | 18,46 | |
| 3,1 | 1,76 | 1,2 | 2,11 | 3,1 | 1,44 | 1,353 | -0,153 | 0,0235 | 12,77 | |
| 5,3 | 2,30 | 1,8 | 4,14 | 5,3 | 3,24 | 1,857 | -0,057 | 0,0033 | 3,19 | |
| 7,4 | 2,72 | 2,2 | 5,98 | 7,4 | 4,84 | 2,247 | -0,047 | 0,0022 | 2,12 | |
| 9,6 | 3,10 | 2,6 | 8,06 | 9,6 | 6,76 | 2,599 | 0,001 | 0,0000 | 0,05 | |
| 11,8 | 3,44 | 2,9 | 9,96 | 11,8 | 8,41 | 2,912 | -0,012 | 0,0001 | 0,42 | |
| 14,5 | 3,81 | 3,3 | 12,57 | 14,5 | 10,89 | 3,259 | 0,041 | 0,0017 | 1,20 | |
| 18,7 | 4,32 | 3,8 | 16,43 | 18,7 | 14,44 | 3,740 | 0,060 | 0,0036 | 1,58 | |
| Итого | 71,6 | 22,54 | 18,7 | 60,24 | 71,6 | 50,83 | 18,700 | -0,001 | 0,0619 | 39,82 |
| Среднее значение | 8,95 | 2,82 | 2,34 | 7,53 | 8,95 | 6,35 | – | – | 0,0077 | 4,98 |
|
| – | 1,00 | 0,935 | – | – | – | – | – | – | – |
|
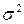
| – | 1,00 | 0,874 | – | – | – | – | – | – | – |
Найдем уравнение регрессии:
,
.
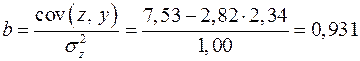Т.е. получаем следующее уравнение регрессии: 
. Теперь заполняем столбцы 8-11 нашей таблицы.
Индекс корреляции находим по формуле (1.21):
,
а индекс детерминации 
, который показывает, что 99,1% вариации результативного признака объясняется вариацией признака-фактора, а 0,9% приходится на долю прочих факторов.
Средняя ошибка аппроксимации: 
показывает, что линия регрессии хорошо приближает исходные данные.
-критерий Фишера:
,
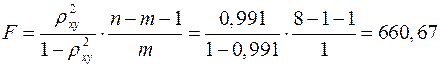значительно превышает табличное .
Изобразим на графике исходные данные и линию регрессии:
Рис. 1.7
Для нахождения параметров регрессии необходимо провести ее линеаризацию, как было показано выше:
,
где .
Составляем вспомогательную таблицу для преобразованных данных:
Таблица 1.7
| 
| 
| 
| 
|
|
|
|
| |
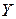
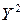
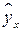
| 0,182 | -0,105 | -0,019 | 0,033 | 0,011 | 0,8149 | 0,0851 | 0,0072 | 9,46 | |
| 1,131 | 0,182 | 0,206 | 1,280 | 0,033 | 1,3747 | -0,1747 | 0,0305 | 14,56 | |
| 1,668 | 0,588 | 0,980 | 2,781 | 0,345 | 1,8473 | -0,0473 | 0,0022 | 2,63 | |
| 2,001 | 0,788 | 1,578 | 4,006 | 0,622 | 2,2203 | -0,0203 | 0,0004 | 0,92 | |
| 2,262 | 0,956 | 2,161 | 5,116 | 0,913 | 2,5627 | 0,0373 | 0,0014 | 1,43 | |
| 2,468 | 1,065 | 2,628 | 6,092 | 1,134 | 2,8713 | 0,0287 | 0,0008 | 0,99 | |
| 2,674 | 1,194 | 3,193 | 7,151 | 1,425 | 3,2165 | 0,0835 | 0,0070 | 2,53 | |
| 2,929 | 1,335 | 3,910 | 8,576 | 1,782 | 3,7004 | 0,0996 | 0,0099 | 2,62 | |
| Итого | 15,315 | 6,002 | 14,637 | 35,035 | 6,266 | 18,608 | 0,0919 | 0,0595 | 35,14 |
| Среднее значение | 1,914 | 0,750 | 1,830 | 4,379 | 0,783 | – | – | 0,0074 | 4,39 |
|
| 0,846 | 0,470 | – | – | – | – | – | – | – |
|
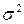
| 0,716 | 0,221 | – | – | – | – | – | – | – |
Найдем уравнение регрессии:
,
.
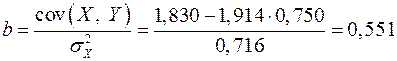Т.е. получаем следующее уравнение регрессии: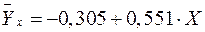 
. После потенцирования находим искомое уравнение регрессии:
.
Теперь заполняем столбцы 7-10 нашей таблицы.
Индекс корреляции находим по формуле (1.21):
,
а индекс детерминации 
, который показывает, что 96,7% вариации результативного признака объясняется вариацией признака-фактора, а 3,3% приходится на долю прочих факторов.
Средняя ошибка аппроксимации: 
показывает, что линия регрессии хорошо приближает исходные данные.
-критерий Фишера:
,
значительно превышает табличное .
Изобразим на графике исходные данные и линию регрессии:
Рис. 1.8.
Сравним построенные модели по индексу детерминации и средней ошибке аппроксимации:
Таблица 1.8
| Модель | Индекс детерминации,  (, )
| Средняя ошибка аппроксимации,  , %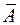
|
Линейная модель, 
| 0,987 | 6,52 |
| Полулогарифмическая модель,
| 0,918 | 14,51 |
| Модель с квадратным корнем,
| 0,991 | 4,98 |
| Степенная модель,
| 0,967 | 4,39 |
Наиболее хорошо исходные данные аппроксимирует модель с квадратным корнем. Но в данном случае, так как индексы детерминации линейной модели и модели с квадратным корнем отличаются всего на 0,004, то вполне можно обойтись более простой линейной функцией.
