Жорамалдарды тексеру әдісі:
1. X1,X2,…,Xn таңдамасына байланысты Н0 нөлдік және Н1 балама жорамалдарды ұйғару.
2. Tn=T(X1,X2,…,Xn) статистикалық критерийін таңдау.
(әдетте: U- қалыпты таралу, Х2- таралу (Пирсонның хи-квадраты), Стьюденттің t- таралуы, Фишердің F-таралуы).
3.Tn статистикалық критерийі және a мәнділік деңгейі бойынша tсыни сыни нүктесін, яғни S аймағын аймағынан бөліп тұратын шекараны анықтайды.
4. Х=(X1,X2,…,Xn) таңдамасының сипаттамалары бойынша критерийдің мәндерін есептейді, яғни Tбақ=T(X1,X2,…,Xn)=t
5. Егер tÎ S (мысалы, S оң жақтағы аймақ үшін t> tсыни.), онда Н0 нөлдік жорамалды жоққа шығарады; ал егер tÎ - S (t <tсыни), онда Н0 жорамалын жоққа шығаруға негіз жоқ.
Стьюдент критерийі.
Салыстырылатын екі орташа мән арасындағы айырмаларды бағалаудың ең таралған параметрлік әдісі Стьюдент критерийі немесе t-критерий болып табылады.
Мұнда екі жағдай болу мүмкін: таңдамалар тәуелсіз және тәуелді болса.
Таңдамалар тәуелсіз болған жағдайда, екі орташаның теңдігі туралы нольдік болжамды тексереміз (яғни екі таңдама бір генеральды жиынтықтан алынған).
Тексерілетін t-критерий сәйкес таңдама орташалардың айырмасының осындай айырманың қатесіне қатынасы түрінде өрнектеледі, яғни
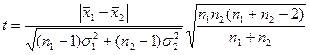
и 
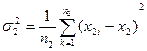немесе
 |
n1=n2=n df=n-1
n1≠n2 df= n1+n2-2
1-мысал. Сау адамдар және гепатитпен ауыратындар тобында қан іркітінде ақуыз құрамы анықталды. Сау адамдар және гепатитпен ауыратындар тобында ақуыз құрамындағы айырмашылық барын анықтау, α=0,05.
| X1 (қалып) | 6,87 | 6,51 | 6,9 | 7,05 | ||
| X2 (гепатит) | 7,2 | 6,92 | 7,52 | 7,18 | 7,25 | 7,1 |
Н0: – сау адамдар және гепатитпен ауыратындар тобында ақуыз құрамындағы айырмашылық жоқ.
Екі таңдамалар орташа мәндерін есептейміз:
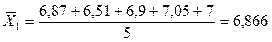
t-критерийді есептейміз:
α=0,05 және (n1-1)+(n2-1)=10 бостандық дәрежелерінің саны үшін tкрит=2,26 деп анықтадық.
tесеп > tкрит (2,67>2,26), яғни нольдік болжам жоққа шығарылады.
Қорытынды: Қалыптағы алынған ақуыз құрамы α=0,05 кезінде гепатит ауруында қанда ақуыз құрамынан статистикалық айырмашылығы бар.
Екі тәуелді таңдаманы немесе жұптаса байланысқан варианталары бар таңдамаларды салыстыру үшін олардың жұп айырмаларының орташа мәнінің нөлге теңдік болжамы тексеріледі. Бұндай жағдай әрбір пациенттің бізді қызықтыратын белгісінде өзгерістер туралы мәліметтер болғанда туындайды. Мысалы, егер пациенттер тобы зерттелетін емдеу тәсілін қолданса және әрбір пациентте емдеуге дейін және емдеуден кейін белгінің мәні өлшеніп отырса. Бұл жағдайда терапияны алу нәтижесінде осы белгінің өзгерістерінің нольге теңдігі туралы нольдік болжамы тексерілу керек. Бұл жағдайда генеральды орташалар арасындағы айырмаларды бағалау ретінде жұп айырмалар суммасынан анықталатын орташа айырма алынады. Орташалар айырмасының генеральды дисперсиясын бағалау болып таңдама дисперсия алынады
Егер бас жиынтық мүшелері қалыпты тарамдалса, онда олардың арасындағы айырмалар да қалыпты тарамдалады. Сондықтан көрсеткіш мәндерінің өзгерісінің нөлге теңдігі туралы нөлдік болжамды тексеру үшін тестілік қатынас есептеледі:
df=n-1
2-мысал. Гипертониямен ауыратын 6 аурудан тұратын топта артериялық қысымын азайтатын адельфан дәрмегінің әсері зерттелді. Тәжірибе нәтижесінде систолиялық қысымның 2 вариациялық қатары алынды: біріншісі – дәрмекті қабылдағанға дейін (бақылау), екіншісі – дәрмекті қабылдағаннан кейін (тәжірибе):
| Бақылау | ||||||
| Тәжірибе |
Адельфанды қабылдағаннан кейін систолиялық артериялық қысым қандай шамаға азаяды? Алынған нәтижелер нақты ма?
Н0: – Адельфанды қабылдағаннан кейін систолиялық артериялық қысымына әсері жоқ.
Біріншіден, жұп айырмаларды есептеп шығамыз:
| xki (бақылау) | хoi (тәжірибе) | di (қысымдар айырмасы) |
| -40 | ||
| -45 | ||
| -45 | ||
| -20 | ||
| -30 | ||
Айырмалар қатары үшін статистикалық параметрлерді есептейміз:
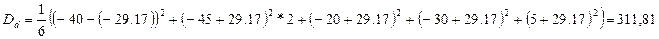
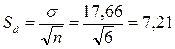
tесеп анықтаймыз:
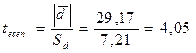
Стьюдент кестесі бойынша Р=0,95 және n-1=5 бостандық дәрежелері саны үшін tкрит=2,57.
tесеп > tкрит – яғни нөлдік болжам жоққа шығарылады.
Қорытынды: Адельфан дәрмегін қабылдау Р>0,95 ықтималдықпен артериялық қысымын 29,17/207,5*100%=14%-ке төмендетеді (
).
t-критерийді дұрыс қолдану үшін салыстырылатын таңдамалар алынып тасталған жиынтықтардың қалыпты тарамдалуы болу керек. Егер бұл шарт орындалмаса, онда параметрлік емес критерийлер тиімді болады.
- Параметрлік емес критерийлер.
Таңдамалардың таралуын қалыптылыққа тексеруді талап етпейтін критерийлерді қарастырайық.
Салыстырылатын тәуелсіз таңдамалардың бір бас жиынтыққа қатысы туралы болжамды тексеру үшін Манн—Уитни U-критерийін келтіреміз.
