На листе.
Для того чтобы занятия графикой не превратились в слепое копирование линий и штрихов, необходимо бегло ознакомиться с самыми простыми правилами композиции. Приблизительное значение слова композиция в перевод на русский язык означает сочинение.
Итак, начинаем с самого простого - компоновки изображения на листе. Очень важно правильно закомпановать предмет на листе. Выбрать такой размер изображения, чтобы ему не было «тесно» в формате листа и, наоборот, чтобы изображение не потерялось.
Человеческий глаз устроен так, что мы не сможем увидеть геометрический центр прямоугольника точно. Большинство людей будет видеть оптический центр «О» несколько выше геометрического центра «К», полученного пересечением диагоналей, и, поэтому, изображение будет закомпановано на листе несколько выше. Расстояние от края изображения до края листа сверху должно быть несколько меньше чем внизу (рис. 7).
Это касается только изображения отдельных абстрактных композиций. Следует знать, что архитектурная графика привязана к человеку, и объекты показываются с точки зрения человека, т.к. линия горизонта находится на уровне глаз, значит она чаще всего расположена ≈ на уровне 168 см над поверхностью земли. Отсюда следует, что линия горизонта будет делить лист на две неравные части, причем земли будет меньше, т.е. архитектурная форма будет располагаться несколько ниже. Это касается уже конкретной архитектурной формы. Однако из этого правила бывают исключения, но мы их рассматривать не будем.
Несколько видов нежелательной компоновки. Изображение не должно касаться края листа (рис. 8, 9).
Рис. 8 Рис. 9
Расстояние от края листа до объекта не должно быть равным его ширине (рис. 10).
 | |||
 |
Рис. 10
Нельзя показывать объект меньше половины (рис. 11). Для показа пространства желательно показать «воздух» с двух сторон от предмета (рис. 12)
Рис. 6 Рис. 7
Перед «лицом» объекта «воздуха» должно быть больше (рис. 13). Иначе создается впечатление «тесноты», «лицом к стене» (рис. 14).
Рис. 13 Рис. 14
Для того, чтобы рисунок хорошо воспринимался, необходимо иметь понятие о равновесии. Нельзя все части изображения перенести на одну сторону листа (рис. 15).
Рис. 15 Рис. 16
Правая часть листа (рис. 15) явно перевешивает, поэтому воспользуемся каким-либо элементом для уравновешивания рисунка (рис. 16).
Следует помнить, что сплошной черный смотрится гораздо тяжелее чем белый. Поэтому одна или несколько маленьких деталей смогут уравновесить большой легкий предмет (рис. 17).
Рис. 17
В этих примерах нет и намека на то, что одну массу можно уравновесить такой же массой. Конечно же, две одинаковые массы будут уравновешивать друг друга, однако, этого не следует делать. Каждая из масс будет претендовать на первое место и в итоге ни одна из них не будет выделена зрителем. Это очень хорошо видно на натюрморте с двумя арбузами (рис. 18). Если провести ось симметрии, мы разделим картину на две равные части, что недопустимо (рис. 19). Изображение должно быть цельным и неделимым.
Рис. 18 Рис. 19
Массы должны отличаться друг от друга. Нельзя делить лист пополам линией горизонта (рис. 20). Нельзя пользоваться диагональю как основой Вашего рисунка (рис. 21).
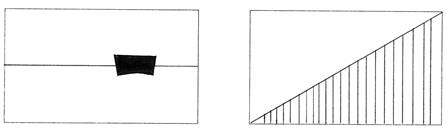
Рис. 20 рис. 21
Лучше выбрать другую наклонную линию, делящую Ваш лист на две неравные части.
Линию в угол желательно не направлять (рис. 22) и не занимать углы. Не стоит отвлекать внимание от основного изображения (рис. 23). А – зона внимания. Б отвлекает внимание от А.
Рис. 22 рис. 23
Наклонные линии характерны не только для передачи движения, но и для передачи эмоционального напряжения, особенно, если верх изображения будет утяжелен тоном (рис. 24, 25).
Рис. 24 Рис. 25
Посвятим несколько слов привязкам. Что это такое? Это линии, которые удерживают изображение нашего предмета на листе (рис. 28). Представим себе шарик на наклонной плоскости. Допустим слегка приподнятый стол с одной стороны. Шарик сразу же постарается скатиться вниз (рис. 26).
Рис. 26 Рис. 27 Рис.28
«Привяжем» шарик одной линией. Теперь он может перемещаться только как маятник (рис. 27). Лишим его и этой возможности двумя линиями. Теперь изображение шарика «привязано» к листу (рис. 28). Следует заметить, что эти линии вовсе не обязательно будут геометрически правильно располагаться. А зависимости от ситуации они могут и не касаться края листа (рис. 29).
Рис. 29
Далее мы ознакомимся с двумя видами композиции. Статичной и динамичной.
Если мы поставим шарик на горизонтальную плоскость, то несмотря на неустойчивость формы шарик останется на месте (рис. 30). Это и будет основа статической композиции. Горизонтальная линия и устойчивая форма яркий пример статики (рис. 31).
Рис. 30 Рис. 31
Если же мы изменим наклон плоскости, шарик начнет двигаться (рис. 32). С этого начинается динамическая композиция, с наклонной линии (рис. 33).
Рис. 32 рис. 33
Видов композиций очень много, но мы с Вами будем рассматривать наиболее простые. Почти в каждой рассматриваемой нами композиции необходимо выделить композиционный центр. Это возможно сделать при помощи тона, ритма, движения. Для этого нужно направить движение к центру композиции (рис. 34) или от него (рис. 35). Следует заметить, что композиционный центр может находиться и за форматом листа. Однако движение все равно будет к центру (рис. 36).
Рис. 34 рис. 35 рис. 36
Сделаем различие между открытой и закрытой композицией. Композиция имеющая возможность развиваться будет называться открытой. Для наглядности приведем пример прибрежной полосы рассматриваемой со стороны воды. Развитие вправо и влево будет бесконечным насколько хватит взора (рис. 37). Это будет открытой композицией.
Рис. 37
 |
или же развитие одинаковых элементов в стороны от центра (рис. 38) и это тоже будет открытая композиция.
Рис. 38
Закрытая композиция это композиция, продолжение которой будет лишним. Примером могут являться эмблемы атома, фирменный знак и т.д. (рис. 39, 40)
 |
Рис. 39 рис. 40
Чтобы из открытой композиции перейти в закрытую достаточно в ряд элементов по краям внести элементы отличные от центра и от развивающегося ряда. Элементы должны быть либо больше, либо меньше (рис. 41, 42). Замыкающие элементы возможно выделить тоном.
Рис. 41 Рис. 42
Желательно избегать точек касания как между формами (рис. 43) так и формы с краем листа (рис. 44). Лучше сделать «наложение» одной формы на другую (рис. 45).
 |
Рис. 43 рис. 44 рис. 45
Необходимо избегать пересечения нескольких линий в одной точке. Появляются так называемые узлы напряжения, их необходимо развести и избежать контакта.
Сравните рисунки 46, 47, в рисунке, 46 лимон, стакан и соломинка пересекаются в одной точке, что негативно сказывается на восприятии. В рисунке 47 этот узел разгрузили. Здесь так же наблюдается отсутствие контакта. Если это не удается сделать, узел лучше закрыть каким-либо пятном (рис. 48, 49).
Рис. 46 рис. 47 рис. 48 Рис. 49
Так же желательно избегать совмещения линий. Попробуем нарисовать домик и совместить линии крыши и линии горизонта (рис. 50, 51). Выйдет очень некрасиво и не совсем понятно. Попробуем развести эти совмещения и рисунок сразу улучшается (рис. 52, 53).
Рис. 50 Рис. 51
Рис. 52 Рис. 53
I.4. Пропорции.
Пропорциями называются размерные отношения двух частей формы. Эти закономерные отношения делятся на две группы: простые отношения, строящиеся на простых, рациональных числах и иррациональные отношения – производные от геометрических построений.
В каждой композиции, в каждой форме должна быть заключена какая-то закономерность. Такое чередование размеров, частей формы, чтобы можно было ею любоваться. Пропорциями определяется соразмерность и гармоничность элементов формы и композиции.
Никто не знает почему, но отношения 3:5 вызывают позитивную реакцию у людей. Предпринимались теоретические и практические объяснения этого факта, однако к единому мнению так и не пришли, но речь об этом не пойдет. Факт заключается в том, что из большого разнообразия прямоугольников с самыми разнообразными отношениями сторон большинство испытуемых людей выбрало прямоугольник с отношениями сторон, характерными для «золотого сечения». Сам термин – «золотое сечение», ввел в научный обиход Леонардо да Винчи.
«Золотое сечение» получается при делении целого на две неравные части таким образом, чтобы целое относилось к большей части так же, как большая часть относиться к меньшей (рис. 54).
Покажем это графически.
Рис. 54
На прямой линии возьмем отрезок АС. Точкой В разделим его на «золотое сечение» с отношением сторон ВС:АВ, т.е. большей к меньшей. Затем поставим иглу циркуля в точку С и проведем дугу до пересечения с прямой в точке К. радиусы одной окружности равны. Стало быть и отрезки АС и СК так же равны, т.е. вновь полученный отрезок СК равен старому АС. Глядя на рисунок, мы с Вами заметим, что отношения нового отрезка СК и большей части старого отрезка ВС равны предыдущим отношениям ВС:АВ. Иначе – целое относится к большей части так, как большая часть относится к меньшей. На этом принципе мы с Вами и будем строить свои композиции и формы. Разглядывая рисунок и представляя дальнейшие построения, легко прийти к выводу, что эти отношения повторяют сами себя, т.е. увеличиваются только размеры, сами же отношения остаются прежними. Этим мы и буде руководствоваться. Если мы запишем размеры длин полученных отрезков, то получим ряд чисел.
3, 5, 8, 13, 21, 34, 55 … и т.д.
Закономерность этого ряда очевидна, здесь каждый последующий член ряда равен сумме двух предыдущих.
3 + 5 = 8, 5 + 8 = 13, 8 + 13 = 21, 13 + 21 = 34, …
На практике часто используется приближенное «золотое сечение». Мы с Вами назовем такие отношения основанными на принципе подобия.
Более сложным пропорциональными отношениями является подобие двух или более частей формы. Два прямоугольника могут быть подобными друг другу тем, что отношения больших сторон к меньшим одинаково. Таким образом, мы будем рассматривать форму как систему прямоугольников с преимущественно вертикальными и горизонтальными членениями. Признаками подобия для них является параллельность или перпендикулярность сторон и диагоналей (рис. 56, 57, 58, 59).
Рис. 56 Рис. 57
Рис. 58 Рис. 59
Если Вы имеете спропорционированный прямоугольник, подобные ему возможно получить следующим образом.
На диагонали поставим любую точку и опустим перпендикуляры на стороны (рис. 60). Мы получим прямоугольник подобный первому. Если пользоваться этим принципом мы сможем получить размеры любого подобного прямоугольника геометрическим способом. Для этого нужно отложить необходимый нам размер на одной из сторон (МК) или на продолжении стороны, если необходим больший прямоугольник и восстановить из этой точки перпендикуляр до пересечения с диагональю (точка «А»). Затем опустим из точки «А» перпендикуляр на другую сторону (рис. 61).
Рис. 60 рис. 61
Не всегда возможно прибегнуть к геометрическим построениям, тогда используют коэффициент 0,6
3: 5 = 0,6
Если у нас есть натуральный размер какого-либо отрезка х, то чтобы построить прямоугольник с меньшей стороной мы умножаем х · 0,6 (рис. 62), если с большей мы разделим х на 0,6; х: 0,6 (рис. 63).
рис. 62 рис. 63
Само «золотое сечение» имеет отношения, которые выражаются дробным числом:
1: 1.62
Геометрические построения выглядят следующим образом (рис. 64). Возьмем прямоугольный треугольник АВС с отношением катетов 1:2, т.е. один катет АВ в два раза больше другого ВС.
рис. 64
В вершину С поставим иглу циркуля и на гипотенузу АС отложим катет ВС – получим точку Д. Затем поставим иглу циркуля в вершину А и перенесем размер АД на катет АВ – получим точку М.
Именно точка М разделит наш катет АВ в отношении «золотого сечения»
АВ: АМ = АМ: МВ
и выражается дробным числом 1: 1.62.
Различаются два вида прямоугольников: статические и динамические. пример статического прямоугольника Вам уже показан. Это прямоугольник состоящий из двух квадратов (рис. 64). К динамическим прямоугольникам относятся прямоугольники с длиной сторон 
, т.е. иррациональные отношения. Их получают геометрическим методом взяв за исходную фигуру квадрат (рис. 65).
рис. 65
Построим квадрат АВСD. Проведем диагональ АС и продлим стороны квадрата ВС и АD. Установим иглу циркуля в вершине а и отложим диагональ квадрата АС на продолжении стороны АD. Из полученной точки М восстановим перпендикуляр до пересечения с продолжением стороны ВС, получим точку К. мы увидим новый правильно спропорционированный прямоугольник АВКМ с длиной длинной стороны АМ равной 
.
Аналогично строятся и остальные прямоугольники. Диагональ опускается на продолжение стороны прямоугольника, восстанавливается перпендикуляр и мы получаем новый прямоугольник.
В задачи этого курса не входит обучение пропорционированию. Вас просто ознакомили с некоторыми видами пропорциональных отношений. Для составления своих форм мы будем пользоваться упрощенными отношениями 3:5, рассмотренными ранее.
Рис. I.4.1
Ранее говорилось о том, что отношения частей отрезков повторяют сами себя (стр. 18 рис. 54). На этом принципе построена данная композиция. Рассмотрим поэтапность ее построения. Вначале у нас имеется прямоугольник с отношением сторон 0,62 (рис. I.4.1а). Разобьем прямоугольник осями с отношением 3:5 (рис. I.4.1б). Каждую вновь полученную часть мы будем делить на те же части, т.е. будем повторять одни и те же отношения (см. рис. I.4.1в - I.4.1е).
Рис. I.4.1а Рис. I.4.1б Рис. I.4.1в
Рис. I.4.1г Рис. I.4.1д Рис. I.4.1е
|
Рис. I.4.2
Рис. I.4.3
Рис. I.4.4 Рис. I.4.5
|
Рис. I.4.6
