ФКЛ-5
Изучение туннельного эффекта с помощью полупроводникового туннельного диода.
Тула, 2011 г
Лабораторная работа.
изучение туннельного эффекта с помощью полупроводникового туннельного диода.
Цель работы: изучение элементов теории туннельного эффекта, исследование проявлений туннельного эффекта в вырожденном p-n переходе (туннельном диоде.
Теоретическое описание.
Физика туннельного эффекта.
Рассмотрим поведение частицы при прохождении через потенциальный барьер. Пусть частица, движущаяся слева направо, встречает на своём пути потенциальный барьер высоты U0 и ширины l (рис. 1.1). По классическим представлениям движение частицы будет таким:
v
|
если энергия частицы будет больше высоты барьера (E>U0), то частица беспрепятственно проходит над барьером;
|
v
|
|
v сквозь барьер частица проникнуть не может.
Совершенно иначе поведение частицы по законам квантовой механики. Во-первых, даже при E>U0 имеется отличная от нуля вероятность того, что частица отразится от потенциального барьера и полетит обратно. Во-вторых, при E<U0 имеется вероятность того, что частица проникнет «сквозь» барьер и окажется в области III. Такое поведение частицы описывается уравнением Шрёдингера:
. (1.1)
Здесь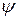 
- волновая функция микрочастицы. Уравнение Шрёдингера для области I и III будет одинаковым. Поэтому ограничимся рассмотрением областей I и II. Итак, уравнение Шрёдингера для области I примет вид:
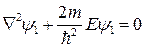, (1.2)
введя обозначение:
, (1.3)
окончательно получим:
(1.4)
Аналогично для области II:
, (1.5)
где 
. Таким образом, мы получили характеристические уравнения, общие решения которых имеют вид:
при x<0, (1.6)
при x>0 (1.7)
Слагаемое 
соответствует волне, распространяющейся в области I в направлении оси х, А1- амплитуда этой волны. Слагаемое 
соответствует волне, распространяющейся в области I в направлении, противоположном х. Это волна, отражённая от барьера, В1- амплитуда этой волны.
По определению коэффициентом отражения называется отношение потока отраженных частиц 
к потоку падающих частиц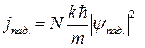 
(где N – число падающих на ступеньку частиц). Поэтому коэффициент отражения в случае, представленном на рис. 1.1 равен:
(1.8)
Слагаемое 
соответствует волне, распространяющейся в области II в направлении х. Слагаемое 
должно соответствовать отражённой волне, распространяющейся в области II. Так как такой волны нет, то В2 следует положить равным нулю.
Отношение 
представляет собой коэффициент прозрачности (коэффициент прохождения) барьера.
Для прямоугольного потенциального барьера, изображенного на рис. 1.1 имеем:
(1.9)
Для барьера, высота которого U>E, волновой вектор k2 является мнимым. Положим его равным ik, где 
является действительным числом. Тогда волновые функции 
и 
приобретут следующий вид: 
(1.10)
(1.11)
Так как 
, то это значит, что имеется вероятность проникновения микрочастицы на некоторую глубину во вторую область. Эта вероятность пропорциональна квадрату модуля волновой функции :
. (1.12)
Наличие этой вероятности делает возможным прохождение микрочастиц сквозь потенциальный барьер конечной толщины а (рис. 1.1). Такое просачивание получило название туннельного эффекта. По формуле (1.11) коэффициент прозрачности такого барьера будет равен:
, (1.13)
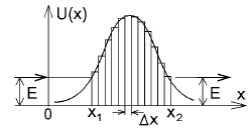где D0 – коэффициент пропорциональности, зависящий от формы барьера. Особенностью туннельного эффекта является то, что при туннельном просачивании сквозь потенциальный барьер энергия микрочастиц не меняется: они покидают барьер с той же энергией, с какой в него входят. Если потенциальный барьер имеет произвольную форму (см. рис. 1.2), то разобьем его на n очень узких прямоугольных потенциальных барьеров шириной Δх и высотой U(x) каждый. Поток частиц, прошедших через узкий потенциальный барьер, будет потоком частиц, падающих на следующий узкий потенциальный барьер.
Поэтому коэффициент прохождения через все барьеры будет произведением коэффициентов прохождения через каждый из барьеров (вероятности перемножаются), показатели экспонент в сомножителях (1.13) складываются и при Δх →dх дают интеграл:
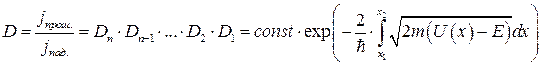(1.14)
Туннельный эффект играет большую роль в электронных приборах. Он обуславливает протекание таких явлений, как эмиссия электронов под действием сильного поля, прохождение тока через диэлектрические плёнки, пробой p-n перехода; на его основе созданы туннельные диоды, работа которых исследуется в данном опыте, разрабатываются активные плёночные элементы.
